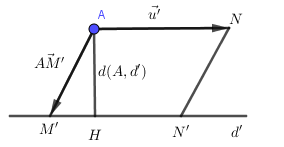
Cho hình vẽ dưới đây, công thức nào không dùng để tính khoảng cách từ điểm \(A\) đến đường thẳng \(d'\)?
Trả lời bởi giáo viên
Quan sát hình vẽ ta thấy: \({S_{AM'N'N}} = \left| {\left[ {\overrightarrow {AN} ,\overrightarrow {AM'} } \right]} \right| = AH.\left| {\overrightarrow {M'N'} } \right| \Rightarrow AH = \dfrac{{\left| {\left[ {\overrightarrow {AN} ,\overrightarrow {AM'} } \right]} \right|}}{{\left| {\overrightarrow {M'N'} } \right|}}\) nên các đáp án A, B, D đều đúng.
Đáp án C sai vì \(\dfrac{{\left| {\left[ {\overrightarrow {AM'} ,\overrightarrow {u'} } \right]} \right|}}{{\left| {\overrightarrow {NN'} } \right|}} = \dfrac{{{S_{AM'N'N}}}}{{\left| {\overrightarrow {NN'} } \right|}} = d\left( {A,NN'} \right)\)
Hướng dẫn giải:
Sử dụng công thức tính diện tích hình bình hành: \({S_{ABCD}} = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right]} \right| = \left| {\overrightarrow {AB} } \right|.d\left( {C,AB} \right) \Rightarrow d\left( {C,AB} \right) = \dfrac{{\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right]} \right|}}{{\left| {\overrightarrow {AB} } \right|}}\)

