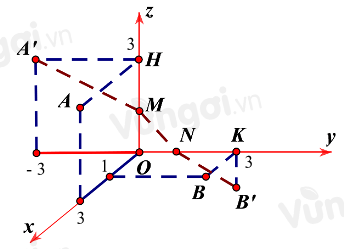
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {3;0;3} \right)\) và \(B\left( {1;3;0} \right)\). Điểm \(M\) di động trên tia \(Oz\), điểm \(N\) di động trên tia \(Oy\). Đường gấp khúc \(AMNB\) có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục)
Trục \(Oz\) đi qua điểm \(O\left( {0;0;0} \right)\) và có vectơ chỉ phương \(\vec k\left( {0;0;1} \right)\).
Suy ra phương trình trục \(Oz\) là: \(\left\{ \begin{array}{l}x = 0\\y = 0\\z = t\end{array} \right.\).
Gọi \(\left( \alpha \right)\) là mặt phẳng chứa điểm \(A\) và vuông góc với trục \(Oz\).
Suy ra \(\left( \alpha \right)\) nhận \(\vec k\left( {0;0;1} \right)\) làm vectơ pháp tuyến.
Mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\left( {3;0;3} \right)\) và có vectơ pháp tuyến \(\vec k\left( {0;0;1} \right)\).
Suy ra phương trình mặt phẳng \(\left( \alpha \right)\): \(0.\left( {x - 3} \right) + 0.\left( {y - 0} \right) + 1.\left( {z - 3} \right) = 0\)
\( \Leftrightarrow z - 3 = 0\).
Gọi \(H\) là giao điểm của trục \(Oz\) và mặt phẳng \(\left( \alpha \right)\).
Ta có \(H \in Oz \Rightarrow H\left( {0;0;t} \right)\).
Lại có \(H \in \left( \alpha \right) \Rightarrow t = 3\).
Khi đó \(H\left( {0;0;3} \right)\).
Chứng minh tương tự, ta tìm được hình chiếu của điểm \(B\) lên trục \(Oy\) là \(K\left( {0;3;0} \right)\).
Chọn \(A'\left( {0; - 3;3} \right) \in \left( {Oyz} \right)\) và \(B'\left( {0;3; - 1} \right) \in \left( {Oyz} \right)\).
Xét \(\Delta AHM\) và \(\Delta A'HM\), có:
\(HM\) chung.
\(AH = A'H\,\,\left( { = 3} \right)\).
\(\widehat {AHM} = \widehat {A'HM} = 90^\circ \).
Do đó \(\Delta AHM = \Delta A'HM\) (c.g.c)
\( \Rightarrow AM = A'M\) (cặp cạnh tương ứng)
Chứng minh tương tự, ta được \(BN = B'N\).
Trong mặt phẳng \(\left( {Oyz} \right)\), ta có độ dài đường gấp khúc \(AMNB\) là:
\(AM + MN + NB = A'M + MN + NB' \ge A'B' = 2\sqrt {13} \).
Khi đó độ dài nhỏ nhất của đường gấp khúc \(AMNB\) là \(2\sqrt {13} \approx 7,21\).
Vậy ta chọn phương án A.
Trong không gian tọa độ \(Oxyz\), cho hình thang cân \(ABCD\) có các cạnh đáy lần lượt là \(AB,CD\). Biết \(A\left( {3;1; - 2} \right)\), \(B\left( { - 1;3;2} \right),C\left( { - 6;3;6} \right)\) và \(D\left( {a;b;c} \right)\) với \(a,b,c \in \mathbb{R}\). Tính \(T = a + b + c\).
Ta có:
\(\begin{array}{l}\overrightarrow {AB} = \left( { - 4;2;4} \right),\,\,\,\overrightarrow {CD} = \left( {a + 6;b - 3;c - 6} \right)\\\overrightarrow {AD} = \left( {a - 3;b - 1;c + 2} \right),\,\,\overrightarrow {BA} = \left( {4; - 2; - 4} \right),\,\,\,\overrightarrow {BC} = \left( { - 5;0;4} \right)\end{array}\).
Từ giác \(ABCD\) là hình thang cân \( \Rightarrow \overrightarrow {CD} = k\overrightarrow {AB} \Leftrightarrow \dfrac{{a + 6}}{{ - 4}} = \dfrac{{b - 3}}{2} = \dfrac{{c - 6}}{4}\)
\( \Leftrightarrow \left\{ \begin{array}{l}2\left( {a + 6} \right) = - 4\left( {b - 3} \right)\\a + 6 = - \left( {c - 6} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + 6 = - 2\left( {b - 3} \right)\\a + 6 = - c + 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 2b\\c = 2b\end{array} \right.\)
Lại có \(\angle DAB = \angle CBA\) nên \(\left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right)\)
\(\begin{array}{l} \Leftrightarrow \dfrac{{ - 4\left( {a - 3} \right) + 2\left( {b - 1} \right) + 4\left( {c + 2} \right)}}{{\sqrt {{4^2} + {2^2} + {4^2}} .\sqrt {{{\left( {a - 3} \right)}^2} + {{\left( {b - 1} \right)}^2} + {{\left( {c + 2} \right)}^2}} }} = \dfrac{{4.\left( { - 5} \right) + \left( { - 2} \right).0 + \left( { - 4} \right).4}}{{\sqrt {{4^2} + {2^2} + {4^2}} .\sqrt {{5^2} + {0^2} + {4^2}} }}\\ \Leftrightarrow \dfrac{{ - 4a + 2b + 4c + 18}}{{6\sqrt {{{\left( {a - 3} \right)}^2} + {{\left( {b - 1} \right)}^2} + {{\left( {c + 2} \right)}^2}} }} = \dfrac{{ - 36}}{{6\sqrt {41} }}\\ \Leftrightarrow \left( { - 4a + 2b + 4c + 18} \right)\sqrt {41} = - 36\sqrt {{{\left( {a - 3} \right)}^2} + {{\left( {b - 1} \right)}^2} + {{\left( {c + 2} \right)}^2}} \end{array}\)
Thay \(a = - 2b,\,\,c = 2b\) vào phương trình trên ta được:
\(\begin{array}{l}\left( { - 4.\left( { - 2b} \right) + 2b + 4.2b + 18} \right)\sqrt {41} = - 36\sqrt {{{\left( { - 2b - 3} \right)}^2} + {{\left( {b - 1} \right)}^2} + {{\left( {2b + 2} \right)}^2}} \\ \Leftrightarrow \left( {18b + 18} \right)\sqrt {41} = - 36\sqrt {4{b^2} + 12b + 9 + {b^2} - 2b + 1 + 4{b^2} + 8b + 4} \\ \Leftrightarrow \left( {b + 1} \right)\sqrt {41} = - 2\sqrt {9{b^2} + 18b + 14} \Leftrightarrow \left\{ \begin{array}{l}b + 1 < 0\\41{\left( {b + 1} \right)^2} = 4\left( {9{b^2} + 18b + 14} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}b < - 1\\5{b^2} + 10b - 15 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b < - 1\\\left[ \begin{array}{l}b = 1\\b = - 3\end{array} \right.\end{array} \right. \Leftrightarrow b = - 3\\ \Rightarrow a = 6,c = - 6 \Rightarrow a + b + c = - 3.\end{array}\)
Trong không gian với hệ tọa độ $Oxyz$, cho hai vectơ $\overrightarrow a = \left( {1;1; - 2} \right)$, $\overrightarrow b = \left( { - 3;0; - 1} \right)$ và điểm $A\left( {0;2;1} \right)$. Tọa độ điểm $M$ thỏa mãn $\overrightarrow {AM} = 2\overrightarrow a - \overrightarrow b $ là:
Ta có $2\overrightarrow a - \overrightarrow b = \left( {5;2; - 3} \right)$. Gọi \(M\left( {x;y;z} \right)\), suy ra $\overrightarrow {AM} = \left( {x;y - 2;z - 1} \right)$.
Theo giả thiết, suy ra \(\left\{ \begin{array}{l}x = 5\\y - 2 = 2\\z - 1 = - 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 5\\y = 4\\z = - 2\end{array} \right.\).
Trong không gian với hệ tọa độ \(Oxyz\), cho ba vectơ \(\overrightarrow a = \left( {1;0; - 2} \right)\,,\,{\rm{ }}\overrightarrow b = \left( { - 2;1;3} \right)\), \(\,\overrightarrow c = \left( { - 4;3;5} \right)\). Tìm hai số thực \(m\), \(n\) sao cho \(m.\overrightarrow a + n.\overrightarrow b = \overrightarrow c \) ta được:
Ta có \(m.\overrightarrow a + n.\overrightarrow b = \left( {m - 2n;\,n; - 2m + 3n} \right)\).
Suy ra \(m.\overrightarrow a + n.\overrightarrow b = \overrightarrow c \Leftrightarrow \left\{ \begin{array}{l}m - 2n = - 4\\n = 3\\ - 2m + 3n = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 2\\n = 3\end{array} \right..\)
Trong không gian với hệ tọa độ $Oxyz$, cho bốn điểm $A\left( {2;0;0} \right),{\rm{ }}B\left( {0;2;0} \right),{\rm{ }}C\left( {0;0;2} \right)$ và $D\left( {2;2;2} \right)$. Gọi $M,{\rm{ }}N$ lần lượt là trung điểm của \(AB\) và $CD$. Tọa độ trung điểm $I$ của $MN$ là:
$M$ là trung điểm của $AB$ suy ra tọa độ điểm $M\left( {1;1;0} \right)$.
$N$ là trung điểm của $CD$ suy ra tọa độ điểm $N\left( {1;1;2} \right)$.
$I$ là trung điểm của $MN$ suy ra tọa độ điểm $I\left( {1;1;1} \right)$.
Trong không gian $Oxyz$ cho tam giác $ABC$ với điểm $A\left( { - 1; - 2;3} \right),B\left( {0;3;1} \right)$ và $C\left( {4;2;2} \right)$. Gọi $M,N$ lần lượt là trung điểm các cạnh $AB,AC$. Độ dài đường trung bình $MN$ bằng:
Có \(\overrightarrow {BC} = (4; - 1;1)\). Suy ra \(BC = 3\sqrt 2 \).
Theo tính chất đường trung bình có \(MN = \dfrac{1}{2}BC = \dfrac{{3\sqrt 2 }}{2}\).
Trong không gian với hệ tọa độ \(Oxyz\), cho ba vectơ
\(\overrightarrow a = \left( { - 1;1;0} \right)\), \(\overrightarrow b = \left( { - 2; - 2;0} \right)\) và \(\overrightarrow c = \left( {1;1;1} \right).\)
Trong các khẳng định sau, khẳng định nào sai?
Ta có \(\left| {\overrightarrow a } \right| = \sqrt {1 + 1 + 0} = \sqrt 2 \); \(\left| {\overrightarrow c } \right| = \sqrt {1 + 1 + 1} = \sqrt 3 .\)
Xét \(\overrightarrow a .\overrightarrow b = \left( { - 1} \right).\left( { - 2} \right) + 1.\left( { - 2} \right) + 0.0 = 0\), suy ra \(\overrightarrow a \bot \overrightarrow b .\)
Vậy đáp án còn lại D là sai.
Trong không gian với hệ tọa độ \(Oxyz\), cho hai vectơ
$\overrightarrow u = \left( {m; - 2;m + 1} \right)$ và $\overrightarrow v = \left( {0;m - 2;1} \right)$.
Tất cả giá trị của \(m\) có thể có để hai vectơ $\overrightarrow u $ và $\overrightarrow v $ cùng phương là:
Ta có $\overrightarrow u $ và $\overrightarrow v $ cùng phương $ \Leftrightarrow \exists k \in \mathbb{R}:{\rm{ }}\overrightarrow u = k\overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}m = 0\\ - 2 = k\left( {m - 2} \right)\\m + 1 = k\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 0\\k = 1\end{array} \right..$
Trong không gian với hệ tọa độ \(Oxyz\), cho sáu điểm \(A\left( {1;2;3} \right)\), \(B\left( {2; - 1;1} \right)\), \(C\left( {3;3; - 3} \right)\), \(A',\,\,B',\,\,C'\) thỏa mãn \(\overrightarrow {A'A} + \overrightarrow {B'B} + \overrightarrow {C'C} = \overrightarrow 0 \). Nếu \(G'\) là trọng tâm tam giác \(A'B'C'\) thì \(G'\) có tọa độ là:
Gọi \(G'\left( {x;y;z} \right)\) là trọng tâm của tam giác \(A'B'C'\).
Ta có \(\overrightarrow {G'A'} + \overrightarrow {G'B'} + \overrightarrow {G'C'} = \overrightarrow 0 \Leftrightarrow \left( {\overrightarrow {G'A} + \overrightarrow {AA'} } \right) + \left( {\overrightarrow {G'B} + \overrightarrow {BB'} } \right) + \left( {\overrightarrow {G'C} + \overrightarrow {CC'} } \right) = \overrightarrow 0 \)\( \Leftrightarrow \overrightarrow {G'A} + \overrightarrow {G'B} + \overrightarrow {G'C} = \overrightarrow {A'A} + \overrightarrow {B'B} + \overrightarrow {C'C} = \overrightarrow 0 \).
Suy ra \(G'\) cũng là trọng tâm của tam giác \(ABC\) nên có tọa độ \(\left( {2;\dfrac{4}{3};\dfrac{1}{3}} \right).\)
Trong không gian với hệ tọa độ \(Oxyz\), cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 2,{\rm{ }}\left| {\overrightarrow b } \right| = 5\) và \(\left( {\overrightarrow a ,\overrightarrow b } \right) = {30^0}\). Độ dài của vectơ \(\left[ {\overrightarrow a ,\overrightarrow b } \right]\) bằng:
Áp dụng công thức \(\left| {\left[ {\overrightarrow a ,\overrightarrow b } \right]} \right| = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\sin \left( {\overrightarrow a ,\overrightarrow b } \right)\), ta được \(\left| {\left[ {\overrightarrow a ,\overrightarrow b } \right]} \right| = 2.5.\sin {30^0} = 5.\)
Trong không gian với hệ tọa độ \(Oxyz\), cho các điểm \(A,\,{\rm{ }}B,{\rm{ }}\,C\) có tọa độ thỏa mãn \(\overrightarrow {OA} = \overrightarrow i + \overrightarrow j + \overrightarrow k \), \(\overrightarrow {OB} = 5\overrightarrow i + \overrightarrow j - \overrightarrow k \), \(\overrightarrow {BC} = 2\overrightarrow i + 8\overrightarrow j + 3\overrightarrow k \). Tọa độ điểm \(D\) để tứ giác \(ABCD\) là hình bình hành là:
Ta có \(A\left( {1;1;1} \right)\), \(B\left( {5;1; - 1} \right)\) và \(\overrightarrow {BC} = \left( {2;8;3} \right)\). Suy ra tọa độ điểm \(C\left( {7;9;2} \right)\).
Gọi \(D\left( {x;y;z} \right)\). Vì \(ABCD\) là hình bình hành nên
\(\overrightarrow {CD} = \overrightarrow {BA} \) \( \Leftrightarrow \left\{ \begin{array}{l}x = {x_A} + {x_C} - {x_B}\\y = {y_A} + {y_C} - {y_B}\\z = {z_A} + {z_C} - {z_B}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 9\\z = 4\end{array} \right.\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hình bình hành $ABCD$ với $A\left( {1;0;1} \right)$, $B\left( {2;1;2} \right)$ và giao điểm của hai đường chéo là $I\left( {\dfrac{3}{2};0;\dfrac{3}{2}} \right)$. Diện tích của hình bình hành $ABCD$ bằng:
Do $ABCD$ là hình bình hành nên $I$ là trung điểm của $BD$, suy ra $D\left( {1; - 1;1} \right)$.
Ta có $\left\{ \begin{array}{l}\overrightarrow {AB} = \left( {1;1;1} \right)\\\overrightarrow {AD} = \left( {0; - 1;0} \right)\end{array} \right. \Rightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right] = \left( {1;0; - 1} \right)$
Diện tích của hình bình hành: \({S_{ABCD}} = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right]} \right| = \sqrt {{1^2} + {0^2} + {{\left( { - 1} \right)}^2}} = \sqrt 2 \)
Trong không gian với hệ tọa độ \(Oxyz\), cho tam giác \(ABC\) có \(A\left( {2; - 1;6} \right)\), \(B\left( { - 3; - 1; - 4} \right)\), \(C\left( {5; - 1;0} \right)\). Tam giác \(ABC\) là
Ta có \(A{B^2} = 125;\,A{C^2} = 45;\,B{C^2} = 80\)
Do đó $A{B^2} = C{A^2} + C{B^2} \Rightarrow \Delta ABC$ vuông tại \(C\).
Trong không gian với hệ tọa độ \(Oxyz\), cho tam giác \(ABC\). Tập hợp các điểm \(M\) thỏa mãn \(\left[ {\left( {\overrightarrow {MA} + \overrightarrow {MB} } \right),\overrightarrow {AC} } \right] = \overrightarrow 0 \) là:
Gọi \(I\) là trung điểm của \(AB\), ta có \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \).
Khi đó \(\left[ {\left( {\overrightarrow {MA} + \overrightarrow {MB} } \right),\overrightarrow {AC} } \right] = \overrightarrow 0 \)\( \Leftrightarrow \left[ {2\overrightarrow {MI} ,\overrightarrow {AC} } \right] = \overrightarrow 0 \).
Suy ra \(\overrightarrow {MI} \) cùng phương với \(\overrightarrow {AC} \).
Trong không gian với hệ tọa độ \(Oxyz\), cho ba vectơ $\overrightarrow u = \left( {2; - 1;1} \right)$, $\overrightarrow v = \left( {m;3; - 1} \right)$ và $\overrightarrow w = \left( {1;2;1} \right)$. Để ba vectơ đã cho đồng phẳng khi \(m\) nhận giá trị nào sau đây?
Ta có: $\left[ {\overrightarrow u ,\overrightarrow w } \right] = \left( { - 3; - 1;5} \right)$
Để ba vectơ đồng phẳng thì $\left[ {\overrightarrow u ,\overrightarrow w } \right].\overrightarrow v = 0 \Leftrightarrow - 3m - 3 - 5 = 0 \Leftrightarrow m = - \dfrac{8}{3}.$
Trong không gian với hệ tọa độ \(Oxyz\), cho bốn điểm \(A\left( {1; - 2;0} \right)\), \(B\left( {1;0; - 1} \right)\), \(C\left( {0; - 1;2} \right)\) và \(D\left( {0;m;p} \right)\). Hệ thức giữa \(m\) và \(p\) để bốn điểm \(A,\,{\rm{ }}B,\,{\rm{ }}C,\,{\rm{ }}D\) đồng phẳng là:
Ta có \(\overrightarrow {AB} = \left( {0;2; - 1} \right)\), \(\overrightarrow {AC} = \left( { - 1;1;2} \right)\), \(\overrightarrow {AD} = \left( { - 1;m + 2;p} \right)\).
Suy ra $\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {5;1;2} \right)$
Để bốn điểm \(A,\,{\rm{ }}B,\,{\rm{ }}C,\,{\rm{ }}D\) đồng phẳng thì \(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD} = 0\)\( \Leftrightarrow m + 2p = 3\).
Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm
$A\left( {1;2; - 1} \right),{\rm{ }}B\left( {2;1;1} \right),{\rm{ }}C\left( {0;1;2} \right)$. Gọi $H\left( {a;b;c} \right)$ là trực tâm của tam giác \(ABC\). Giá trị của $a + b + c$ bằng:
Ta có $\left\{ \begin{array}{l}\overrightarrow {AH} = \left( {a - 1;b - 2;c + 1} \right)\\\overrightarrow {BH} = \left( {a - 2;b - 1;c - 1} \right)\end{array} \right.$ và $\left\{ \begin{array}{l}\overrightarrow {AB} = \left( {1; - 1;2} \right)\\\overrightarrow {AC} = \left( { - 1; - 1;3} \right)\\\overrightarrow {BC} = \left( { - 2;0;1} \right)\end{array} \right. \Rightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( { - 1; - 5; - 2} \right)$.
Do $H$ là trực tâm của tam giác \(ABC\)
$ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC} = 0\\\overrightarrow {BH} .\overrightarrow {AC} = 0\\\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AH} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2\left( {a - 1} \right) + \left( {c + 1} \right) = 0\\ - 1\left( {a - 2} \right) - 1\left( {b - 1} \right) + 3\left( {c - 1} \right) = 0\\ - 1\left( {a - 1} \right) - 5\left( {b - 2} \right) - 2\left( {c + 1} \right) = 0\end{array} \right.$
$ \Leftrightarrow \left\{ \begin{array}{l} - 2a + c = - 3\\ - a - b + 3c = 0\\ - a - 5b - 2c = - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 1\\c = 1\end{array} \right.$.
Do đó $a + b + c = 4$.
Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A\left( {1;1;1} \right)\), \(B\left( { - 1;1;0} \right)\), \(C\left( {3;1; - 1} \right)\). Điểm \(M\) trên mặt phẳng $\left( {Oxz} \right)$ cách đều ba điểm \(A,{\rm{ }}B,{\rm{ }}C\) có tọa độ là:
Gọi \(M\left( {x;0;z} \right) \in \left( {Oxz} \right)\).
Yêu cầu bài toán \( \Leftrightarrow \left\{ \begin{array}{l}MA = MB\\MA = MC\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}M{A^2} = M{B^2}\\M{A^2} = M{C^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{\left( {1 - x} \right)^2} + {\left( {1 - 0} \right)^2} + {\left( {1 - z} \right)^2} = {\left( { - 1 - x} \right)^2} + {\left( {1 - 0} \right)^2} + {\left( {0 - z} \right)^2}\\{\left( {1 - x} \right)^2} + {\left( {1 - 0} \right)^2} + {\left( {1 - z} \right)^2} = {\left( {3 - x} \right)^2} + {\left( {1 - 0} \right)^2} + {\left( { - 1 - z} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5/6\\z = - 7/6\end{array} \right..\)
Trong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \(C\left( {4;0;0} \right)\) và \(B\left( {2;0;0} \right)\). Tìm tọa độ điểm \(M\) thuộc trục tung sao cho diện tích tam giác \(MBC\) bằng \(3\).
Điểm \(M \in Oy\) nên \(M\left( {0;m;0} \right)\). Ta có \(\overrightarrow {BM} = \left( { - 2;m;0} \right)\), \(\overrightarrow {BC} = \left( {2;0;0} \right)\).
Suy ra \(\left[ {\overrightarrow {BM} ,\overrightarrow {BC} } \right] = \left( {0;0; - 2m} \right)\). Theo giả thiết
${S_{\Delta MBC}} = 3 \Leftrightarrow \dfrac{1}{2}\left| {\left[ {\overrightarrow {BM} ,\overrightarrow {BC} } \right]} \right| = 3 \Leftrightarrow \dfrac{1}{2}\left| { - 2m} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}m = 3\\m = - 3\end{array} \right. \Rightarrow \left[ \begin{array}{l}M\left( {0;3;0} \right)\\M\left( {0; - 3;0} \right).\end{array} \right.$.
Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm \(A(0;2; - 1)\) , \(B(2;0;1)\). Tìm tọa độ điểm $M$ thuộc trong mặt phẳng $\left( {Oyz} \right)$ sao cho :\(M{A^2} + M{B^2}\) đạt giá trị bé nhất.
$M$ thuộc trong mặt phẳng $\left( {Oyz} \right)$, giả sử \(M(0;m;n)\).
Ta có:
\(\begin{array}{l}MA = \sqrt {{{(0 - 0)}^2} + {{(m - 2)}^2} + {{(n + 1)}^2}} = \sqrt {{{(m - 2)}^2} + {{(n + 1)}^2}} \\MB = \sqrt {{{(0 - 2)}^2} + {{(m - 0)}^2} + {{(n - 1)}^2}} = \sqrt {{m^2} + {{(n - 1)}^2} + 4} \end{array}\)
Suy ra
\(\begin{array}{l}M{A^2} + M{B^2} = {(m - 2)^2} + {(n + 1)^2} + {m^2} + {(n - 1)^2} + 4\\ = 2{m^2} - 4m + 2{n^2} + 10 = 2({m^2} - 2m + 1) + 2{n^2} + 8\\ = 2{(m - 1)^2} + 2{n^2} + 8 \ge 8\end{array}\)
\( \Rightarrow \min \left( {M{A^2} + M{B^2}} \right) = 8 \Leftrightarrow \left\{ \begin{array}{l}m - 1 = 0\\n = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 1\\n = 0\end{array} \right.\).
Vậy \(M(0;1;0)\)

