Trong không gian \(Oxyz\), cho hai điểm \(A\left( {3;0;3} \right)\) và \(B\left( {1;3;0} \right)\). Điểm \(M\) di động trên tia \(Oz\), điểm \(N\) di động trên tia \(Oy\). Đường gấp khúc \(AMNB\) có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục)

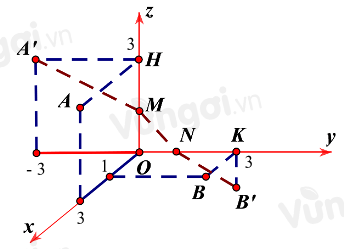
Trục \(Oz\) đi qua điểm \(O\left( {0;0;0} \right)\) và có vectơ chỉ phương \(\vec k\left( {0;0;1} \right)\).

Suy ra phương trình trục \(Oz\) là: \(\left\{ \begin{array}{l}x = 0\\y = 0\\z = t\end{array} \right.\).

Gọi \(\left( \alpha  \right)\) là mặt phẳng chứa điểm \(A\) và vuông góc với trục \(Oz\).

Suy ra \(\left( \alpha  \right)\) nhận \(\vec k\left( {0;0;1} \right)\) làm vectơ pháp tuyến.

Mặt phẳng \(\left( \alpha  \right)\) đi qua điểm \(A\left( {3;0;3} \right)\) và có vectơ pháp tuyến \(\vec k\left( {0;0;1} \right)\).

Suy ra phương trình mặt phẳng \(\left( \alpha  \right)\): \(0.\left( {x - 3} \right) + 0.\left( {y - 0} \right) + 1.\left( {z - 3} \right) = 0\)

\( \Leftrightarrow z - 3 = 0\).

Gọi \(H\) là giao điểm của trục \(Oz\) và mặt phẳng \(\left( \alpha  \right)\).

Ta có \(H \in Oz \Rightarrow H\left( {0;0;t} \right)\).

Lại có \(H \in \left( \alpha  \right) \Rightarrow t = 3\).

Khi đó \(H\left( {0;0;3} \right)\).

Chứng minh tương tự, ta tìm được hình chiếu của điểm \(B\) lên trục \(Oy\) là \(K\left( {0;3;0} \right)\).

Chọn \(A'\left( {0; - 3;3} \right) \in \left( {Oyz} \right)\) và \(B'\left( {0;3; - 1} \right) \in \left( {Oyz} \right)\).

Xét \(\Delta AHM\) và \(\Delta A'HM\), có:

\(HM\) chung.

\(AH = A'H\,\,\left( { = 3} \right)\).

\(\widehat {AHM} = \widehat {A'HM} = 90^\circ \).

Do đó \(\Delta AHM = \Delta A'HM\) (c.g.c)

\( \Rightarrow AM = A'M\) (cặp cạnh tương ứng)

Chứng minh tương tự, ta được \(BN = B'N\).

Trong mặt phẳng \(\left( {Oyz} \right)\), ta có độ dài đường gấp khúc \(AMNB\) là:

\(AM + MN + NB = A'M + MN + NB' \ge A'B' = 2\sqrt {13} \).

Khi đó độ dài nhỏ nhất của đường gấp khúc \(AMNB\) là \(2\sqrt {13}  \approx 7,21\).

Vậy ta chọn phương án A.