Hàm số nào sau đây có thể có đồ thị dạng như hình vẽ?
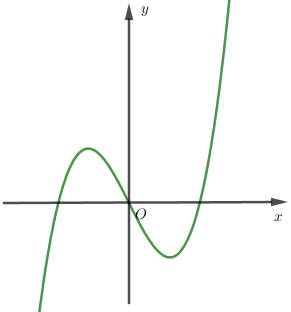
Đồ thị có dạng như hình bên là của hàm đa thức bậc ba.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
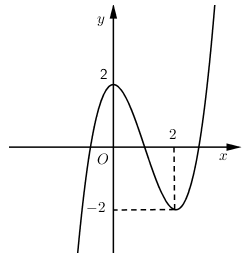
Nhận xét: Đường cong trong hình vẽ là đồ thị của hàm số bậc 3 có hệ số $a > 0$ nên loại đáp án A, C
Xét 2 đáp án B và D
Thay $x = 0;\,y = 2$ thì cả 2 đáp án B, D đều thỏa mãn
Thay $x = 2;\,y = - 2$ chỉ có đáp án B thỏa mãn
Đường cong như hình vẽ là đồ thị của hàm số nào?
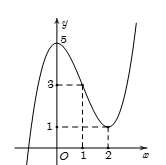
Đồ thị hàm số đã cho là hàm đa thức bậc ba có \(a > 0\) do \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \Rightarrow \) Loại đáp án A.
Đồ thị hàm số đi qua điểm \(\left( {2;1} \right) \Rightarrow \) Loại các đáp án B và D.
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
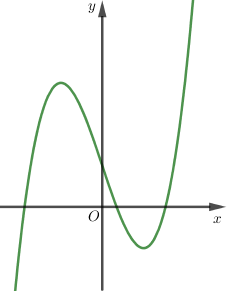
Dựa vào hình dạng đồ thị:
+ Đồ thị hàm số có dạng chữ “N” $ \Rightarrow $ Đồ thị hàm số bậc 3
+ Khi $x \to {\rm{\;}} + \infty $ thì $y \to {\rm{\;}} + \infty {\rm{\;}} \Rightarrow $ Hệ số của ${x^3}$ là dương
Từ hai kết luận trên ta thấy chỉ có hàm số $y = {x^3} - 3x + 1$ thỏa mãn
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
Đồ thị là dạng của hàm số ba, nhánh cuối của đồ thị đi lên \( \Rightarrow \) hệ số của \({x^3}\) mang dấu dương.
Cho hàm số $y = f\left( x \right)$ có đồ thị $\left( C \right)$ như hình vẽ. Hỏi $\left( C \right)$ là đồ thị của hàm số nào?
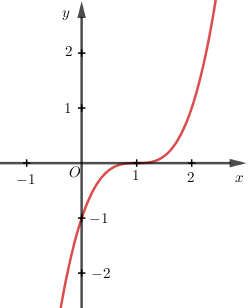
Từ đồ thị ta quan sát thấy $y\left( 0 \right) = - 1,y\left( 1 \right) = 0$ do đó loại A và C.
Hàm số bậc ba nhận nghiệm của phương trình y’’=0 làm tâm đối xứng. Đồ thị đối xứng qua điểm A (1; 0) nên phương trình y’’=0 có nghiệm x = 1.
Đáp án D ta có: $y' = 3{x^2} \Rightarrow y'' = 6x = 0 \Leftrightarrow x = 0 \ne 1 \Rightarrow $ D sai
Do đó chỉ có hàm số $y = {\left( {x - 1} \right)^3}$ thỏa mãn.
Đồ thị trong hình dưới là đồ thị của một trong bốn hàm số cho trong các phương án sau đây, đó là hàm số nào?
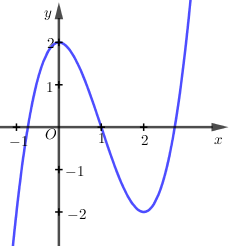
Ta sử dụng theo cách trắc nghiệm để giải bài toán
Hàm số có nét cuối đi lên nên ta có: $a > 0$. Nên ta loại đáp án A.
Đồ thị hàm số đi qua điểm $A(1;0) $ ta thay tọa độ điểm A vào 3 đáp án B, C, D thì đáp án D loại.
Đồ thị hàm số đi qua điểm $B(0;2)$ nên ta thay tọa độ điểm B vào đáp án B và C thì ta loại được đáp án C.
Hàm số nào có thể có dạng như hình vẽ?
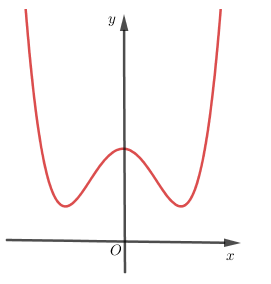
Dạng đồ thị đã cho có thể là hàm bậc bốn trùng phương.
Đường cong trong hình bên là đồ thị của một trong bốn hàm số nào sau đây?
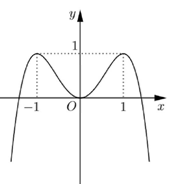
Dựa vào đồ thị hàm số ta thấy hàm số có 3 điểm cực trị nên hàm số cần tìm là hàm số bậc $4 \Rightarrow $ loại đáp án C và D.
Đồ thị hàm số hướng xuống dưới nên hệ số $a < 0 \Rightarrow $ loại đáp án B.
Đường cong hình bên là đồ thị hàm số nào sau đây:
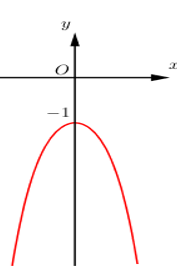
Dễ thấy $\mathop {\lim }\limits_{x \to + \infty } {\mkern 1mu} y = \mathop {\lim }\limits_{x \to - \infty } {\mkern 1mu} y = - \infty \Rightarrow a < 0 \Rightarrow $ Loại A và B.
Đồ thị hàm số đi qua $\left( {0; - 1} \right) \Rightarrow $ Loại C.
Đồ thị sau đây là của hàm số nào ?
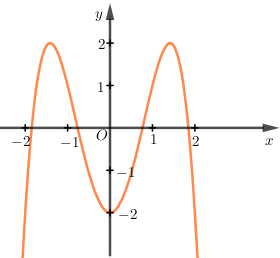
Dựa vào hình vẽ, ta thấy rằng :
Hàm số là hàm số trùng phương, có dạng $y = a{x^4} + b{x^2} + C.$
Giới hạn $\mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} + {\kern 1pt} \infty } {\mkern 1mu} y = \mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} - \infty } {\mkern 1mu} y = - {\mkern 1mu} \infty $$ \Rightarrow $ Hệ số $a < 0.$
Đồ thị hàm số cắt trục Oy tại $\left( {0; - {\mkern 1mu} 2} \right)$$ \Rightarrow $$c = - {\mkern 1mu} 2.$
Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt. Hàm số có ba điểm cực trị, trong đó có điểm cực trị có hoành độ lớn hơn 1.
Vậy hàm số cần tìm là $y = - {\mkern 1mu} {x^4} + 4{x^2} - 2.$
Hàm số nào trong bốn hàm số sau có bảng biến thiên như hình vẽ bên?
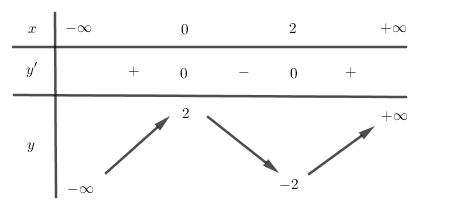
Từ bảng biến thiên ta thấy:
- Đồ thị hàm số đi qua điểm $\left( {0;2} \right)$ nên loại B, D.
- Đồ thị hàm số đi qua điểm $\left( {2; - 2} \right)$ nên thay $x = 2$ vào hi hàm số A và C ta được:
Đáp án A: $y = {2^3} - 3.2 + 2 = 4 \ne - 2$ nên loại A.
Đáp án C: $y = {2^3} - {3.2^2} + 2 = - 2$ nên đáp án C đúng.
Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số nào có bảng biến thiên như sau?
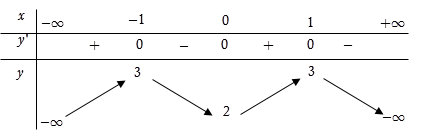
Dựa vào BBT và các phương án lựa chọn, ta thấy:
Đây là dạng hàm số trùng phương có hệ số $a < 0$. Loại A và C.
Mặt khác, đồ thị hàm số đi qua điểm \(\left( {0;2} \right)\) nên loại B.
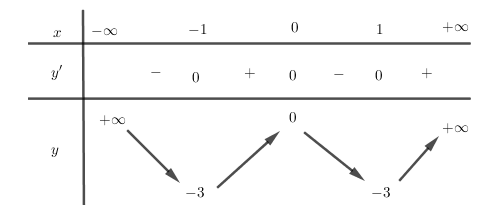
Cho bảng biến thiên của hàm số y = f(x). Mệnh đề nào sau đây sai?
Hàm số đã cho có $\mathop {\lim }\limits_{x \to {\rm{\;}} \pm \infty } y = {\rm{\;}} - \infty $ nên không có GTNN trên tập ℝ
Cho hàm số $y = f\left( x \right) = a{x^4} + {b^2}{x^2} + 1\left( {a > 0} \right)$ . Trong các khẳng định dưới đây, khẳng định nào là sai?
Dễ thấy, đồ thị hàm số luôn đi qua điểm \(\left( {0;1} \right)\) cố định nên A đúng.
Đồ thị hàm số không có tâm đối xứng nên B đúng.
Có \(y' = 4a{x^3} + 2{b^2}x = 2x\left( {4a{x^2} + {b^2}} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\4a{x^2} + {b^2} = 0\end{array} \right.\)
Phương trình \(4a{x^2} + {b^2} = 0\) chỉ có thể vô nghiệm nếu \(b \ne 0\) và có nghiệm duy nhất \(x = 0\) nếu \(b = 0\).
Do đó phương trình \(y' = 0\) chỉ có nghiệm duy nhất \(x = 0\) và \(y'\) đổi dấu qua nghiệm đó nên hàm số chỉ có duy nhất \(1\) điểm cực trị (cụ thể là điểm cực tiểu) nên C đúng.
D sai vì đồ thị hàm số đa thức bậc bốn trùng phương không có tâm đối xứng.
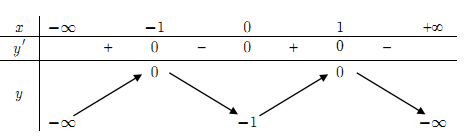
Cho hàm số $y = f(x)$ liên tục trên R và có bảng biến thiên
Khẳng định nào sau đây đúng?
- Tại $x = 0$, y’ chuyển từ dấu dương sang dấu âm, đồng thời $x = 0$ xác định giá trị một giá trị của y = 0
=> Đáp án A: Hàm số đạt cực đại tại $x = 0$ là đúng.
- Hàm số có 3 điểm cực trị => Đáp án B sai.
- Hàm số không có GTLN => Đáp án C sai.
- Hàm số có giá trị cực tiếu bằng -3 => Đáp án D sai.
Cho hàm số $y = a{x^3} + b{x^2} + cx + d$, với a, b, c, d là các số thực và $a$ khác 0 (có đồ thị như hình vẽ). Khẳng định nào sau đây sai?
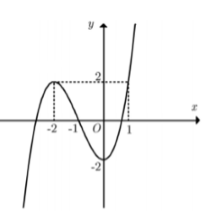
Đáp án A đúng. Ta thấy hàm số nghịch biến trên $\left( {0;2} \right) \Rightarrow y' < 0{\mkern 1mu} {\mkern 1mu} \forall x \in \left( {0;2} \right)$.
Đáp án B sai. Hàm số không có GTLN.
Đáp án C đúng. Hàm số có hai điểm cực trị $x = {\rm{\;}} - 2$ và $x = 0$.
Đáp án D đúng
Cho hàm số $f(x) = a{x^3} + b{x^2} + cx + d$$\left( {a,b,c,d \in \mathbb{R},a \ne 0} \right)$ có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng ?
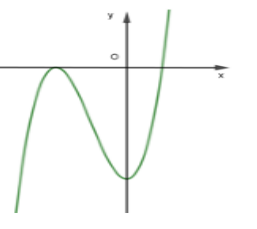
Ta có : $f(x) = a{x^3} + b{x^2} + cx + d$; $f'(x) = 3a{x^2} + 2bx + c$
Do $f(x) \to + \infty $ khi $x \to + \infty $ nên $a > 0$
Do đồ thị hàm số$f(x)$ có hai điểm cực trị là $\left( {{x_0};0} \right)$ và $\left( {0;{y_0}} \right)$ với ${x_0} < 0$ và ${y_0} < 0$
Nên : $\left\{ {\begin{array}{*{20}{l}}{f(0) = {y_0} < 0}\\{f\left( {{x_0}} \right) = 0}\\{f'\left( 0 \right) = 0}\\{f'\left( {{x_0}} \right) = 0}\end{array}} \right.$
Ta có : $\left\{ {\begin{array}{*{20}{l}}{f(0) = d}\\{f'(0) = c}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{d < 0}\\{c = 0}\end{array}} \right.$ ;
+ $f'\left( {{x_0}} \right) = 0$$ \Leftrightarrow 3a{x_0}^2 + 2b{x_0} = 0$$ \Leftrightarrow {x_0} = \dfrac{{ - 2b}}{{3a}}$ Mà ${x_0} < 0$;$a > 0$ $ \Rightarrow b > 0$
Vậy, $a > 0;b > 0;c = 0;d < 0$
Cho hàm số $y = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?
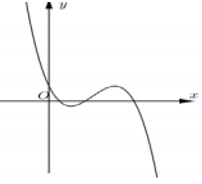
Vì $y \to - \infty $ khi $x \to {\rm{\;}} + \infty $ nên $a < 0$
Đồ thị hàm số cắt Oy tại điểm có tung độ dương $ \Rightarrow d > 0$
Có $y' = 3a{x^2} + 2bx + c = 0$ có $2$ nghiệm dương ($2$ điểm cực trị của đồ thị hàm số có hoành độ dương) $ \Rightarrow b$ trái dấu với $a$ và $c$ cùng dấu với $a$$ \Rightarrow b > 0$ và $c < 0$
Hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?
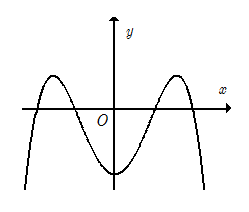
Đồ thị hàm số thể hiện \(a < 0.\)
Đồ thị hàm số có ba điểm cực trị nên \(ab < 0 \Rightarrow b > 0\)
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên \(c < 0.\)
Vậy \(a < 0,{\rm{ }}b > 0,{\rm{ }}c < 0\)

