Câu hỏi:
2 năm trước
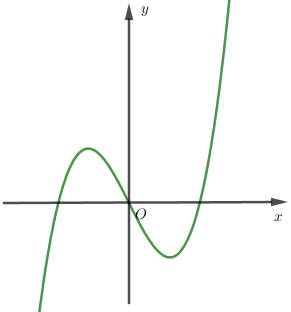
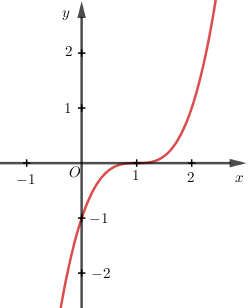
Cho hàm số $y = f\left( x \right)$ có đồ thị $\left( C \right)$ như hình vẽ. Hỏi $\left( C \right)$ là đồ thị của hàm số nào?
Trả lời bởi giáo viên
Đáp án đúng: b
Từ đồ thị ta quan sát thấy $y\left( 0 \right) = - 1,y\left( 1 \right) = 0$ do đó loại A và C.
Hàm số bậc ba nhận nghiệm của phương trình y’’=0 làm tâm đối xứng. Đồ thị đối xứng qua điểm A (1; 0) nên phương trình y’’=0 có nghiệm x = 1.
Đáp án D ta có: $y' = 3{x^2} \Rightarrow y'' = 6x = 0 \Leftrightarrow x = 0 \ne 1 \Rightarrow $ D sai
Do đó chỉ có hàm số $y = {\left( {x - 1} \right)^3}$ thỏa mãn.
Hướng dẫn giải:
Dùng kết quả nếu đồ thị hàm số $y = f\left( x \right)$ đi qua điểm $\left( {a,b} \right)$ thì $b = f\left( a \right)$ và tính đối xứng của đồ thị để loại trừ các trường hợp không xảy ra.
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
