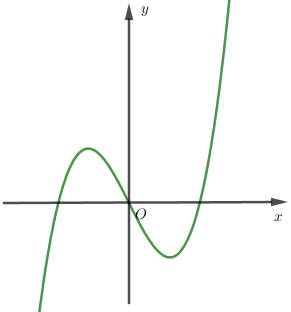
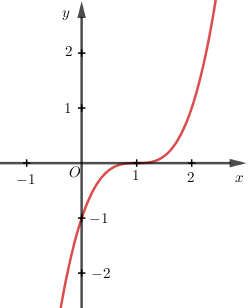
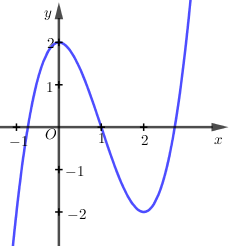
Cho hàm số $f(x) = a{x^3} + b{x^2} + cx + d$$\left( {a,b,c,d \in \mathbb{R},a \ne 0} \right)$ có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng ?
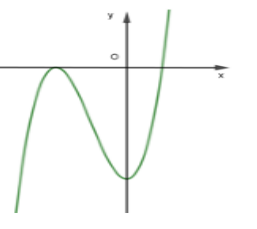
Trả lời bởi giáo viên
Ta có : $f(x) = a{x^3} + b{x^2} + cx + d$; $f'(x) = 3a{x^2} + 2bx + c$
Do $f(x) \to + \infty $ khi $x \to + \infty $ nên $a > 0$
Do đồ thị hàm số$f(x)$ có hai điểm cực trị là $\left( {{x_0};0} \right)$ và $\left( {0;{y_0}} \right)$ với ${x_0} < 0$ và ${y_0} < 0$
Nên : $\left\{ {\begin{array}{*{20}{l}}{f(0) = {y_0} < 0}\\{f\left( {{x_0}} \right) = 0}\\{f'\left( 0 \right) = 0}\\{f'\left( {{x_0}} \right) = 0}\end{array}} \right.$
Ta có : $\left\{ {\begin{array}{*{20}{l}}{f(0) = d}\\{f'(0) = c}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{d < 0}\\{c = 0}\end{array}} \right.$ ;
+ $f'\left( {{x_0}} \right) = 0$$ \Leftrightarrow 3a{x_0}^2 + 2b{x_0} = 0$$ \Leftrightarrow {x_0} = \dfrac{{ - 2b}}{{3a}}$ Mà ${x_0} < 0$;$a > 0$ $ \Rightarrow b > 0$
Vậy, $a > 0;b > 0;c = 0;d < 0$
Hướng dẫn giải:
Sử dụng cách đọc đồ thị hàm số.