Câu hỏi:
2 năm trước
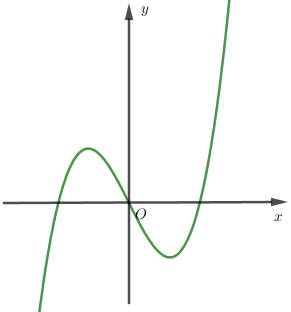
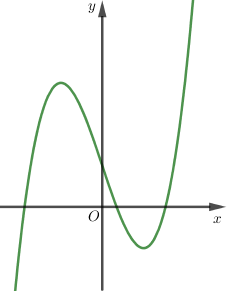
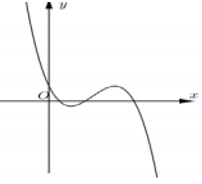
Cho hàm số $y = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?
Trả lời bởi giáo viên
Đáp án đúng: d
Vì $y \to - \infty $ khi $x \to {\rm{\;}} + \infty $ nên $a < 0$
Đồ thị hàm số cắt Oy tại điểm có tung độ dương $ \Rightarrow d > 0$
Có $y' = 3a{x^2} + 2bx + c = 0$ có $2$ nghiệm dương ($2$ điểm cực trị của đồ thị hàm số có hoành độ dương) $ \Rightarrow b$ trái dấu với $a$ và $c$ cùng dấu với $a$$ \Rightarrow b > 0$ và $c < 0$
Hướng dẫn giải:
Quan sát đồ thị, xét các đặc điểm của đồ thị: cắt Ox,Oy, cực đại, cực tiểu,…từ đó suy ra điều kiện a,b,c,d.
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
