Đồ thị hàm số bên là đồ thị của hàm số \(y = {x^4} - 4{x^2} + 1\left( C \right).\) Tìm m để phương trình \({x^4} - 4{x^2} + 1 - m = 0\) có \(2\) nghiệm phân biệt
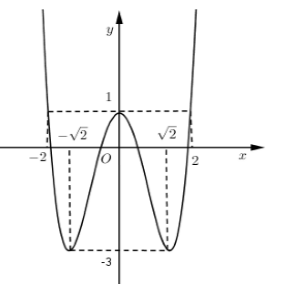
\({x^4} - 4{x^2} + 1 - m = 0 \Leftrightarrow {x^4} - 4{x^2} + 1 = m\)
Số nghiệm của phương trình \({x^4} - 4{x^2} + 1 - m = 0\) là số giao diểm của đồ thị hàm số \(y = {x^4} - 4{x^2} + 1 - m\) và đường thẳng \(y = m\).
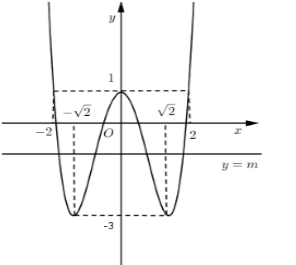
Vậy để phương trình \({x^4} - 4{x^2} + 1 - m = 0\) có \(2\) nghiệm phân biệt \( \Leftrightarrow m > 1\) hoặc \(m = - 3\)
Cho hàm số $y = - {x^4} + 2{{\rm{x}}^2} + 1$ có đồ thị như hình bên
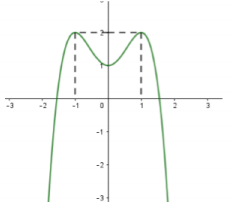
Tìm tất cả các giá trị thực của tham số $m$ để phương trình $ - {x^4} + 2{{\rm{x}}^2} + 1 = m$ có \(3\) nghiệm phân biệt
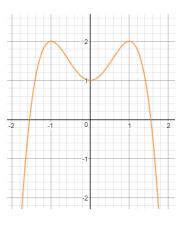
Xét : $ - {x^4} + 2{{\rm{x}}^2} + 1 = m$
Số nghiệm của phương trình bằng số giao điểm của đồ thị hai hàm số $y = - {x^4} + 2{{\rm{x}}^2} + 1;y = m$
Nhìn đồ thị ta thấy khi \(m = 1\) thì đường thẳng \(y = 1\) cắt đồ thị hàm số đã cho tại đúng \(3\) điểm
Cho hàm số $y = f(x)$ có đạo hàm cấp một $f'(x)$ và đạo hàm cấp hai $f''(x)$ trên $\mathbb{R}$. Biết đồ thị hàm số $y = f(x),{\mkern 1mu} {\mkern 1mu} y = f'(x),{\mkern 1mu} y = f''(x)$ là một trong các đường cong $({C_1}),({C_2}),({C_3})$ ở hình vẽ bên. Hỏi đồ thị hàm số $y = f(x),{\mkern 1mu} {\mkern 1mu} y = f'(x),{\mkern 1mu} y = f''(x)$ lần lượt theo thứ tự nào dưới đây?
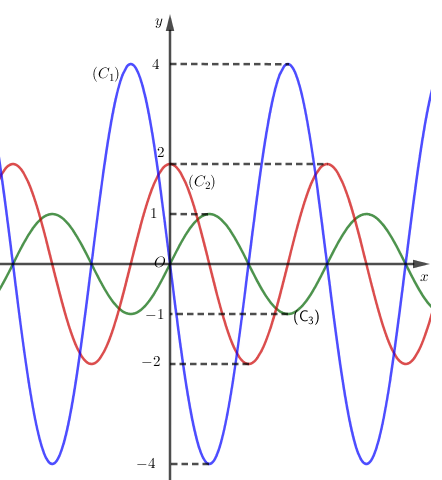
Quan sát dáng đồ thị các hàm số ta thấy đều có dạng đường hình \(\sin \) nên ta dự đoán các hàm số ở đây có thể là dạng \(y = \sin ax\) hoặc \(y = \cos ax\)
Thấy rằng hai đồ thị \(\left( {{C_1}} \right),\left( {{C_3}} \right)\) đi qua điểm \(O\left( {0;0} \right)\) nên một trong hai đồ thị hàm số \(\left( {{C_1}} \right),\left( {{C_3}} \right)\) sẽ là của hàm \(y = f\left( x \right) = \sin ax\), đồ thị \(\left( {{C_2}} \right)\) là của \(y = f'\left( x \right)\) nên loại A và C.
Ta xét hàm số \(y = f\left( x \right) = \sin ax\) có \(f'\left( x \right) = a.\cos ax,f''\left( x \right) = - {a^2}\sin ax\)
Dễ thấy \(f'\left( 0 \right) = a > 0\).
Quan sát các giá trị trên đồ thị ta dễ dàng nhận ra \(a = 2\).
Vậy ta có các hàm số \(y = \sin 2x,y = 2\cos 2x,y = - 4\sin 2x\) lần lượt có đồ thị là \(\left( {{C_3}} \right),\left( {{C_2}} \right),\left( {{C_1}} \right)\)
Vậy \(\left( {{C_3}} \right),\left( {{C_2}} \right),\left( {{C_1}} \right)\) là đồ thị hàm số \(y = f\left( x \right),y = f'\left( x \right),y = f''\left( x \right)\)
Cho các dạng đồ thị (I), (II), (III), (IV) như hình dưới đây:
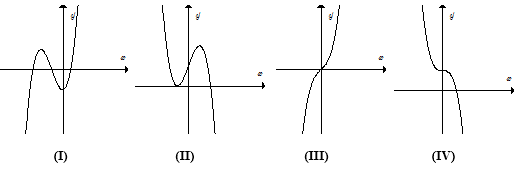
Liệt kê tất cả các dạng có thể biểu diễn đồ thị hàm số \(y = {x^3} + b{x^2} + cx + d\).
Hàm số \(y = {x^3} + b{x^2} + cx + d\) có hệ số của \({x^3}\) dương nên loại (II) và (IV).
Xét \(y' = 3{x^2} + 2bx + c\) có \(\Delta ' = {b^2} - 3c\).
Ta chưa xác định được \(\Delta {'_{y'}}\) mang dấu gì nên có thể xảy ra trường hợp (I) và cũng có thể xảy ra trường hợp (III).
Đề thi THPT QG 2019 – mã đề 104
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên ?
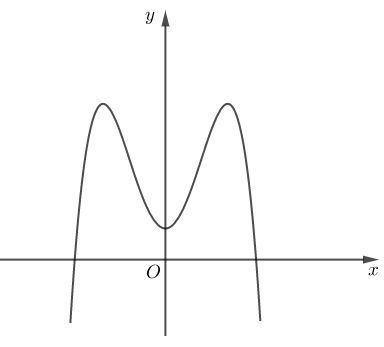
Dựa vào hình dáng đồ thị hàm số ta thấy đây không phải là hàm đa thức bậc ba \( \Rightarrow \) Loại đáp án A; D.
Ta có \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \) nên loại đáp án C.
Biết rằng hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a\not = 0} \right)\) có đồ thị là một trong các dạng dưới đây:
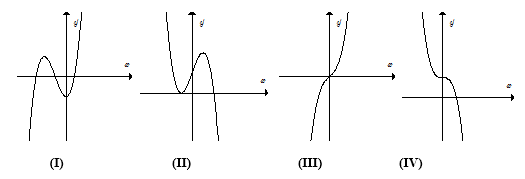
Mệnh đề nào sau đây là đúng?
Đáp án A sai vì đồ thị (I) xảy ra thì \(a > 0\)
Đáp án B sai vì đồ thị (II) xảy ra thì \(a < 0\)
Đáp án C đúng.
Đáp án D sai vì đồ thị (IV) xảy ra thì \(a < 0\)
Đề thi THPT QG – 2021 lần 1– mã 104
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
Đồ thị hàm số bậc \(3\) có hệ số \(a < 0\) và đồ thị cắt trục tung tại điểm có tung độ dương nên \(d > 0\)
Đề thi THPT QG - 2021 - mã 101
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
Đồ thị là dạng của hàm số bậc 4 trùng phương, nhánh cuối của đồ thị đi xuống \( \Rightarrow \) hệ số của \({x^4}\) mang dấu âm.
Đường cong trong hình bên dưới là đồ thị của hàm số nào dưới đây?
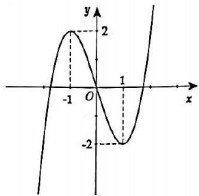
Từ đồ thị hàm số ta có các điểm \(\left( { - 1;2} \right),\left( {1; - 2} \right)\) thuộc đồ thị
Thay tọa độ các điểm trên vào các hàm số ở các đáp án \(A,B,C,D\)
Ta thấy chỉ có hàm số \(y = {x^3} - 3x\)thỏa mãn.
(Vì \(2 = {\left( { - 1} \right)^3} - 3.\left( { - 1} \right); - 2 = {1^3} - 3.1\))
Nên hàm số cần tìm là \(y = {x^3} - 3x\)
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
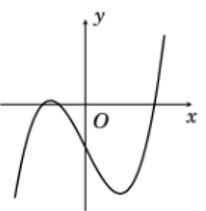
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có nét cuối đi lên nên \(a > 0 \Rightarrow \) loại đáp án D.
Hàm số có 2 điểm cực trị và cắt trục hoành tại 2 điểm phân biệt \( \Rightarrow \) Hàm số là hàm bậc 3 \( \Rightarrow \) loại đáp án A và C.
Hàm số nào dưới đây có đồ thị như trong hình bên?
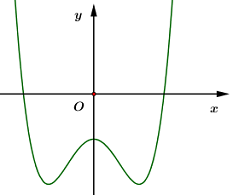
Dựa vào đồ thị hàm số ta thấy hàm số của đồ thị là hàm số bậc 4
\( \Rightarrow \) Loại đáp án A và B.
Ta thấy nét cuối của đồ thị hàm số đi lên nên \(a > 0.\)
\( \Rightarrow \) Loại đáp án C.
Hàm số nào sau đây có đồ thị như hình bên ?
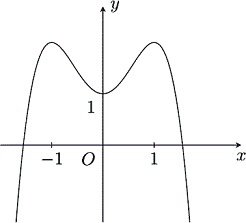
Dựa vào đồ thị ta suy ra đây là đồ thị của hàm bậc 4 dạng trùng phương nên có dạng \(y = a{x^4} + b{x^2} + c\).
+) \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow a < 0\), loại đáp án B và D.
+) Hàm số có 3 điểm cực trị nên \(ab < 0\), mà \(a < 0 \Rightarrow b > 0\), loại đáp án A.
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị hàm số như hình bên. Khẳng định nào sau đây là đúng?
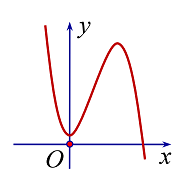
Quan sát đồ thị hàm số, ta thấy:
+) \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow a < 0\).
+) Đồ thị hàm số cắt Oy tại điểm có tung độ dương nên \(d > 0\).
+) Ta có: \(f'\left( x \right) = 3a{x^2} + 2bx + c\).
Hàm số có 2 cực trị: \({x_1} = 0,\,\,{x_2} > 0\), đây là 2 nghiệm phân biệt của phương trình \(f'\left( x \right) = 0\).
\(x = 0\) là nghiệm của phương trình \(f'\left( x \right) = 0 \Rightarrow c = 0\).
Phương trình \(f'\left( x \right) = 0\) có tổng 2 cực trị dương nên \( - \dfrac{b}{{3a}} > 0\), mà \(a < 0\) \( \Rightarrow b > 0\).
Vậy \(a < 0\), \(b > 0\), \(c = 0\), \(d > 0\).
Cho đồ thị (C) của hàm số \(y = {x^3} - 3{x^2} + 3\) như hình vẽ. Hãy xác định số điểm cực trị của hàm số \(y = \left| {{x^3} - 3{x^2} + 3} \right|\).
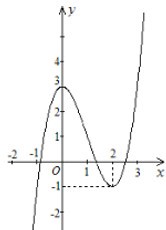
Từ đồ thị hàm số \(y = {x^3} - 3{x^2} + 3\) ta suy ra được đồ thị hàm số \(y = \left| {{x^3} - 3{x^2} + 3} \right|\) như sau (phần nét liền):
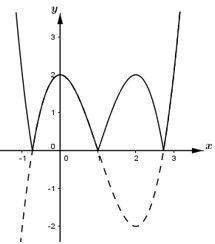
Dựa vào đồ thị hàm số ta thấy hàm số \(y = \left| {{x^3} - 3{x^2} + 3} \right|\) có 5 điểm cực trị.
Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị là đường cong như hình vẽ.
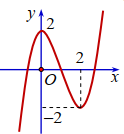
Tính tổng \(S = a + b + c + d\).
Ta có \(f'\left( x \right) = 3a{x^2} + 2bx + c\).
Dựa vào đồ thị hàm số ta thấy:
Đồ thị hàm số đi qua các điểm \(\left( {0;2} \right),\,\,\left( {2; - 2} \right)\).
Đồng thời đây cũng là 2 điểm cực trị của hàm số. Do đó ta có hệ phương trình:
\(\left\{ \begin{array}{l}f\left( 2 \right) = - 2\\f'\left( 2 \right) = 0\\f\left( 0 \right) = 2\\f'\left( 0 \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8a + 4b + 2c + d = - 2\\12a + 4b + c = 0\\d = 2\\c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 3\\c = 0\\d = 2\end{array} \right.\).
Vậy \(S = a + b + c + d = 1 + \left( { - 3} \right) + 0 + 2 = 0\).
Hình dưới đây là đồ thị của hàm số nào?

Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có dạng là 1 parabol có đỉnh là \(\left( {0; - 2} \right) \Rightarrow \) loại đáp án A, D.
Đồ thị hàm số đi qua các điểm \(\left( {1;\,\,0} \right)\) và \(\left( { - 1;\,\,0} \right),\) thay tọa độ các điểm này vào công thức hàm số ở đáp án B và C thấy chỉ có đáp án B thỏa mãn.
có 1 điểm cực trị có tọa là \(\left( {0; - 2} \right)\)
Đường cong trong hình bên là đồ thị của hàm số nào?

- Đồ thị hàm số đã cho có dáng của đồ thị hàm bậc bốn trùng phương nên loại A, D.
- Đồ thị hàm số đi qua điểm \(\left( {0; - 1} \right)\) nên B thỏa mãn.
Đề thi THPT QG - 2021 - mã 102
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
Ta có đồ thị là hàm bậc \(4\) trùng phương: \(y = a{x^4} + b{x^2} + c\) (với \(a \ne 0\)) và phần đường cong cuối cùng đi lên nên \(a > 0\).
Đồ thị hàm số cắt trục \(Oy\) tại điểm có tung độ dương nên \(c > 0\)
Suy ra \(y = 2{x^4} - 4{x^2} + 1\)
Hàm số nào có đồ thị như đường cong trong hình dưới đây?
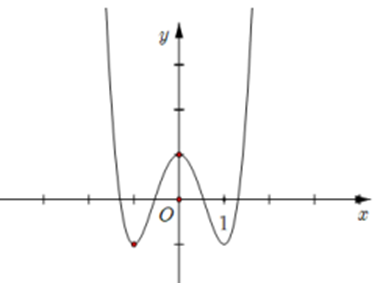
Hàm số đã cho là hàm bậc bốn trùng phương \(y = a{x^4} + b{x^2} + c\).
Vì \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \) nên \(a > 0\). Loại đáp án C.
Đồ thị cắt trục tung tại điểm có tung độ dương nên loại đáp án A.
Hàm số có 3 điểm cực trị nên \(ab < 0\). Mà \(a > 0 \Rightarrow b < 0\). Loại đáp án D.
Cho \(f\left( x \right) = {\left( {x - 1} \right)^3} - 3x + 3\). Đồ thị hình bên là của hàm số có công thức:
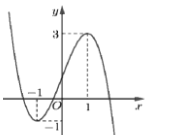
Đáp án A: \(y = - f\left( {x + 1} \right) - 1 = - {x^3} - 3\left( {x + 1} \right) + 3 - 1 = - {x^3} - 3x - 1\). Đồ thị hàm số đi qua điểm \(\left( {0; - 1} \right) \Rightarrow \) Loại.
Đáp án B: \(y = - f\left( {x + 1} \right) + 1 = - {x^3} - 3\left( {x + 1} \right) + 3 + 1 = - {x^3} + 3x + 1\). Đồ thị hàm số đi qua điểm \(\left( {0;1} \right) \Rightarrow \) Đáp án B có thể đúng.
Đáp án C: \(y = - {\left( {x - 2} \right)^3} - 3\left( {x - 1} \right) - 1 = - {x^3} + 6{x^2} - 15x + 10 = 0\). Đồ thị hàm số đi qua điểm \(\left( {0;10} \right) \Rightarrow \) Loại.
Đáp án D: \(y = - {\left( {x - 2} \right)^3} - 3\left( {x - 1} \right) + 1 = - {x^3} + 6{x^2} - 15x + 12 = 0\). Đồ thị hàm số đi qua điểm \(\left( {0;12} \right) \Rightarrow \) Loại.

