Tổng hợp câu hay và khó chương 6 phần 2

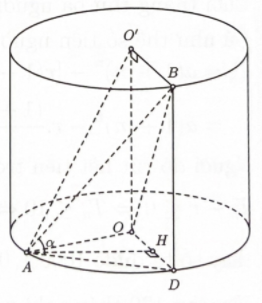
Gọi \(D\) là hình chiếu vuông góc của \(B\) lên mặt phẳng \((O)\).

Kẻ \(AH \bot OD,H \in OD\).

Ta có thể tích của khối chóp \(OO'AB\) là

\({V_{OO'AB}} = \dfrac{1}{3}AH \cdot {S_{\Delta OO'B}} = \dfrac{{2{a^2}}}{3} \cdot AH\)\( \le \dfrac{{2{a^2}}}{3} \cdot AO = \dfrac{{4{a^3}}}{3}\)

\({\left( {{V_{OO'AB}}} \right)_{\max }} \Leftrightarrow H \equiv O\).

Suy ra \(AD = 2\sqrt 2 a\).

Vậy \(\tan \alpha  = \tan \widehat {BAD} = \dfrac{1}{{\sqrt 2 }}\).

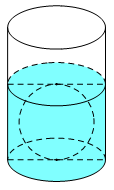
Thể tích mực nước ban đầu là: ${V_1} = \pi r_1^2{h_1} = \pi {.5,4^2}.4,5$

Gọi $R$ là bán kính của viên bi ta có sau khi thả viên bi vào cốc, chiều cao của mực nước bằng $2R,$ do đó tổng thể tích của nước và bi sau khi thả viên bi vào trong cốc là: $V = \pi r_1^2.\left( {2R} \right) = \pi {.5,4^2}.2R$

Thể tích của quả cầu là: ${V_{\left( C \right)}} = \dfrac{4}{3}\pi {R^3}$

Ta có: $V = {V_1} + {V_2} \Leftrightarrow {5,4^2}.4,5 + \dfrac{4}{3}{R^3} = {5,4^2}.2R$

Giải phương trình trên với điều kiện $R < 4,5 \Rightarrow R = 2,7\;cm.$

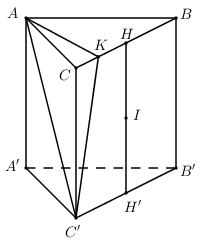
Gọi $H, H’ $ lần lượt là trung điểm của $BC$ và $B’C’$ \( \Rightarrow HH' \bot \left( {ABC} \right)\) và \(HH' \bot \left( {A'B'C'} \right)\).

Gọi $I$ là trung điểm của $HH’.$

Mặt khác \(\Delta ABC\) vuông tại $A,$ \(I \in HH' \Rightarrow \left\{ \begin{array}{l}IA = IB = IC\\IA' = IB' = IC'\end{array} \right.\)

Dễ dàng chứng minh được \(\Delta BHI = \Delta B'H'I\,\,\left( {c.g.c} \right) \Rightarrow IB = IB'\)

\( \Rightarrow IA = IB = IC = IA' = IB' = IC'\) hay $I$ là tâm mặt cầu ngoại tiếp lăng trụ $ABC.A’B’C’.$

Kẻ \(AK \bot BC\) ta có \(AK \bot \left( {BCC'B'} \right) \Rightarrow \widehat {\left( {AC';\left( {BCC'B'} \right)} \right)} = \widehat {\left( {AC';KC'} \right)} = \widehat {AC'K} = {30^0}\).

Có $AC = A'C' = \sqrt {4{a^2} - 3{a^2}}  = a$

Ta có \(AK = \dfrac{{AC.AB}}{{BC}} = \dfrac{{a.a\sqrt 3 }}{{2a}} = \dfrac{{a\sqrt 3 }}{2}\)

\(\begin{array}{l} \Rightarrow AC' = \dfrac{{AK}}{{\sin 30}} = a\sqrt 3 \\ \Rightarrow AA' = \sqrt {AC{'^2} - A'C{'^2}}  = \sqrt {3{a^2} - {a^2}}  = a\sqrt 2  = HH'\\ \Rightarrow HI = \dfrac{1}{2}HH' = \dfrac{a}{{\sqrt 2 }} \Rightarrow BI = \sqrt {{a^2} + \dfrac{{{a^2}}}{2}}  = \dfrac{{a\sqrt 6 }}{2} = R\\ \Rightarrow {S_{mat\,cau}} = 4\pi {\left( {\dfrac{{a\sqrt 6 }}{2}} \right)^2} = 6\pi {a^2}\end{array}\)

Gọi $h,\,\,x$ lần lượt là chiều cao, độ dài cạnh đáy của hình chóp tam giác đều $S.ABC.$

Bán kính đường tròn nội tiếp $\Delta \,ABC$ là  Thể tích khối nón nội tiếp là ${V_1} = \dfrac{1}{3}\pi {r^2}h.$

Bán kính đường tròn ngoại tiếp $\Delta \,ABC$ là  Thể tích khối nón nội tiếp là ${V_2} = \dfrac{1}{3}\pi {R^2}h.$

Vậy tỉ số $\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{{r^2}}}{{{R^2}}} = {\left( {\dfrac{{x\sqrt 3 }}{6}} \right)^2}:{\left( {\dfrac{{x\sqrt 3 }}{3}} \right)^2} = \dfrac{1}{4}.$

Để thể tích gỗ cần phải đẽo đi là ít nhất thì thể tích hình trụ là lớn nhất.

Hay hình trụ là hình trụ nội tiếp hình hộp và có thể tích là ${V_1} = \pi {R^2}h = \dfrac{{\pi {x^2}h}}{4}.$

Với $x$ là độ dài cạnh đáy hình hộp $ \Rightarrow $ Thể tích hình hộp là $V = {x^2}h.$

Suy ra thể tích cần phải đẽo là ${V_2} = V - {V_2} = \left( {1 - \dfrac{\pi }{4}} \right){x^2}h.$

Vậy tỉ lệ thể tích gỗ cần phải đẽo là $\dfrac{{{V_2}}}{V}.100\,\%  = \left( {1 - \dfrac{\pi }{4}} \right).100\,\% \,\, \approx \,\,21,5\,\% .$

Khối cầu ngoại tiếp tứ diện $AB'A'C$ là khối cầu ngoại tiếp lăng trụ $ABC.A'B'C'.$

Bán kính khối cầu ngoại tiếp lăng trụ $ABC.A'B'C'$ là $R = \sqrt {R_{\Delta \,ABC}^2 + \dfrac{{A'{A^2}}}{4}}  = a.$

Vậy thể tích khối cầu cần tính là $V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {a^3}.$

Đường kính đường tròn đáy của một viên phấn là $d = 2r = 2.\dfrac{1}{2} = 1(cm)$  .

Chiều rộng của hộp là $5cm$ $ \Rightarrow $ Xếp được tối đa $5$ viên phấn theo chiều rộng.

Chiều dài của hộp là $30cm$  $ \Rightarrow $ Xếp được tối đa $30$ viên phấn theo chiều dài.

Như vây, có thể xếp được tối đa $5 \times 30 = 150$  viên phấn vào hộp.

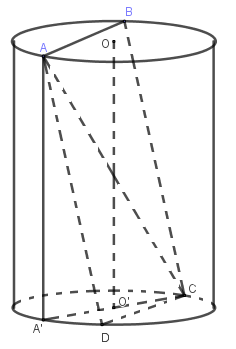
Vì $AB = CD;\,\,AB$//$CD$$ \Rightarrow \,\,ABCD$ là hình chữ nhật $ \Rightarrow \,\,AD = 10\,\,cm.$

Xét hình chữ nhật \(ABCD\) có \(AD\) không song song và không vuông góc với trục \(OO'\) của hình trụ.

Dựng đường sinh $AA'$, ta có \(\left\{ \begin{array}{l}CD \bot AA'\\CD \bot AD\end{array} \right. \Rightarrow CD \bot \left( {AA'D} \right) \Rightarrow CD \bot A'D\)

Suy ra \(A'C\) là đường kính đáy nên \(A'C = 2R\)

Xét tam giác vuông \(AA'C,\) có \(A'C = \sqrt {A{C^2} - A{{A'}^2}}  = \sqrt {{{\left( {2\sqrt {34} } \right)}^2} - {{\left( {6\sqrt 2 } \right)}^2}}  = 8.\)

Suy ra độ dài bán kính đáy của hình trụ là \(2R = 8 \Leftrightarrow R = 4\,\,cm.\)

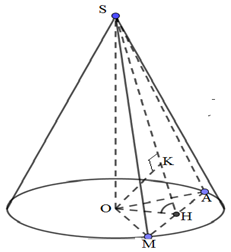
Kẻ $OH\bot AM,\,\,H\in AM,\,\,\,\,\,OK\bot SH,\,\,K\in SH$

Vì  $\left\{ \begin{align}& AM\bot SO \\ & AM\bot OH \\\end{align} \right.\Rightarrow AM\bot (SOH)\Rightarrow AM\bot OK$

Mà $OK \bot SH \Rightarrow OK \bot (SAM) \Rightarrow d(O,(SAM)) = OK = 2$

Ta có: $\left\{ \begin{array}{l}(SAM) \cap (OAM) = AM\\AM \bot (SOH)\end{array} \right.$ (vì $AM \bot OH,\,\,AM \bot SO$)

Mà $(SOH) \cap (OAM) = OH,\,\,(SOH) \cap (SAM) = SH$

$ \Rightarrow \left( {\widehat {(SAM),(OAM)}} \right) = \left( {\widehat {SH,OH}} \right) = \widehat {SHO} = {30^0}$ 

Tam giác OHK vuông tại K $ \Rightarrow OH = \dfrac{{OK}}{{\sin \widehat H}} = \dfrac{2}{{\sin {{30}^0}}} = 4$

Tam giác SOH vuông tại O $ \Rightarrow SO = OH.\tan \widehat H = 4.\tan {30^0} = \dfrac{4}{{\sqrt 3 }}$

Tam giác OAM cân tại O, $\widehat {AOM} = {60^0}$, $OH \bot AM \Rightarrow \widehat {HOM} = \dfrac{{\widehat {AOM}}}{2} = \dfrac{{{{60}^0}}}{2} = {30^0}$

Tam giác OHM vuông tại H $ \Rightarrow OM = \dfrac{{OH}}{{\cos \widehat {HOM}}} = \dfrac{4}{{\cos {{30}^0}}} = \dfrac{4}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{8}{{\sqrt 3 }}$

Thể tích khối nón: $V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi .O{M^2}.SO = \dfrac{1}{3}\pi {\left( {\dfrac{8}{{\sqrt 3 }}} \right)^2}.\dfrac{4}{{\sqrt 3 }} = \dfrac{{256\sqrt 3 \pi }}{{27}}$

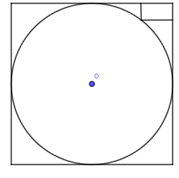
Gắn hệ trục tọa độ trong mặt phẳng chứa đường tròn $(C)$ như hình vẽ.

Phương trình đường tròn $(C):$ ${\left( {x - R} \right)^2} + {\left( {y - R} \right)^2} = {R^2},\,\,\,(R > 2)$

Điểm $\left( {1;2} \right)$ thuộc (C)$ \Rightarrow {\left( {1 - R} \right)^2} + {\left( {2 - R} \right)^2} = {R^2} \Leftrightarrow {R^2} - 6R + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}R = 1\,\,(L)\\R = 5\end{array} \right. \Leftrightarrow R = 5$

$ \Rightarrow $ Chiều cao của khối trụ $h = 2R = 10$

Thể tích khối trụ là: $V = \pi {R^2}h = \pi {.5^2}.10 = 250\pi $.

Vẽ $AH \bot BC$ tại $H,D$ đối xứng với $A$ qua $H$

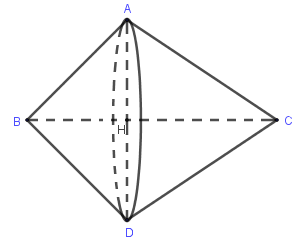
Thể tích khối tròn xoay thu được khi quay $\Delta ABC$ quanh cạnh $BC$ bằng tổng thể tích hai khối nón có chung đường tròn đáy bán kính $AH$. Ta có:

$\dfrac{{3136\pi }}{5} = {V_a} = \dfrac{1}{3}\pi A{H^2}.BH + \dfrac{1}{3}\pi A{H^2}.CH$$ = \dfrac{1}{3}\pi A{H^2}.BC = \dfrac{1}{3}\pi .a.h_a^2$

\( \Rightarrow a{V_a} = \dfrac{1}{3}\pi {a^2}h_a^2 = \dfrac{1}{3}\pi {\left( {2S} \right)^2} = \dfrac{{4\pi }}{3}{S^2}\) với \(S = {S_{ABC}}\).

Tương tự ta có

$\dfrac{{9408\pi }}{{13}} = {V_b} = \dfrac{1}{3}\pi .b.h_b^2 \Rightarrow b{V_b} = \dfrac{{4\pi }}{3}{S^2}$

$672\pi  = {V_c} = \dfrac{1}{3}\pi .c.h_c^2 \Rightarrow c{V_c} = \dfrac{{4\pi }}{3}{S^2}$

$ \Rightarrow a.{V_a} = b.{V_b} = c.{V_c} = \dfrac{{4\pi }}{3}{S^2}\;\left( * \right)$

$ \Rightarrow a:b:c = \dfrac{1}{{{V_a}}}:\dfrac{1}{{{V_b}}}:\dfrac{1}{{{V_c}}} = 15:13:14$

Đặt $a = 15k;b = 13k;c = 14k$. Theo công thức Hêrông, ta có

${S_{ABC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}  = \sqrt {7056{k^2}}  = 84k$ với $p = \dfrac{{a + b + c}}{2} = 21k$

Từ (*) suy ra $\dfrac{{3{V_a}}}{\pi } = \dfrac{{{{\left( {2{S_{ABC}}} \right)}^2}}}{a} \Rightarrow \dfrac{{9408}}{5} = \dfrac{{{{\left( {168k} \right)}^2}}}{{15k}} \Rightarrow k = 1 \Rightarrow {S_{ABC}} = 84$

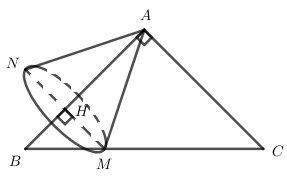
Quay tam giác vuông \(AMH\) quanh trục \(AB\) ta được khối nón có đỉnh \(A\), bán kính đát \(HM\) và đường cao \(AH\) , khi đó ta có thể tích của khối nón tròn xoay \(\left( N \right)\) là \(V = \dfrac{1}{3}\pi H{M^2}.AH\)

Đặt \(HM = x,\,\,\left( {0 \le x \le 12\sqrt 2 } \right)\) ta có \(\Delta BHM\) vuông cân tại \(H\) nên \(BH = HM = x \Rightarrow AH = AB - BH = 12 - x\)

Khi đó \(V = \dfrac{1}{3}\pi {x^2}\left( {12 - x} \right)\)

Xét hàm số \(f\left( x \right) = {x^2}\left( {12 - x} \right)\)  với \(x \in \left[ {0;12\sqrt 2 } \right]\)

\(\begin{array}{l}f'\left( x \right) = 2x\left( {12 - x} \right) - {x^2} =  - 3{x^2} + 24x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 8\end{array} \right.\\\left\{ \begin{array}{l}f\left( 0 \right) = 0\\f\left( {12} \right) = 0\\f\left( 8 \right) = 256\end{array} \right. \Rightarrow \mathop {\max }\limits_{\left[ {0;12\sqrt 2 } \right]} f\left( x \right) = 256\\ \Rightarrow {V_{max}} = \dfrac{1}{3}\pi .256 = \dfrac{{256\pi }}{3}\end{array}\)

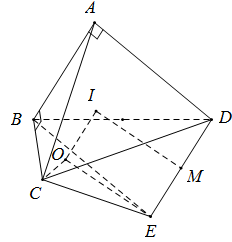
Dựng hình chữ nhật ABED. Ta có mặt cầu tâm I ngoại tiếp tứ diện ABCD cũng phải đi qua điểm E

Do đó I là tâm mặt cầu ngoại tiếp tứ diện BCDE

Ta có AB ⊥ BE; AB ⊥ BC ⇒ AB ⊥ (BCE)

Vì DE // AB nên DE ⊥ (BCE)

Dựng tam giác vuông cân COE trong mặt phẳng (BCE) sao cho B và O nằm cùng phía với CE

Ta chứng minh được O là tâm đường tròn ngoại tiếp ∆ BCE. Dựng hình chữ nhật MEOI với M là trung điểm DE thì I là giao của mặt phẳng trung trực của DE với trục của đường tròn ngoại tiếp ∆ BCE nên I là tâm mặt cầu ngoại tiếp tứ diện $BCDE$

Ta có: $ME = \dfrac{{DE}}{2} = \dfrac{{AB}}{2} = 1$

$OE = \dfrac{{CE}}{{\sqrt 2 }} = \dfrac{{\sqrt {C{D^2} - D{E^2}} }}{{\sqrt 2 }} = \dfrac{{\sqrt {C{D^2} - A{B^2}} }}{{\sqrt 2 }} = \sqrt 2  \Rightarrow IM = OE = \sqrt 2 $ (vì ∆ CED vuông tại E)

$ \Rightarrow R = IE = \sqrt {I{M^2} + M{E^2}}  = \sqrt 3 $

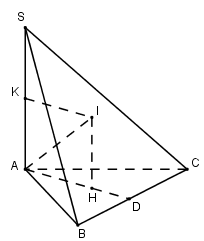
Gọi \(H\) là tâm đường tròn ngoại tiếp tam giác \(ABC\), qua \(H\) kẻ đường thẳng \(d//SA \Rightarrow d \bot \left( {ABC} \right)\)

Gọi \(K\) là trung điểm của \(SA\), qua \(K\) kẻ đường thẳng song song với \(AH\) cắt \(d\) tại \(I\)

\( \Rightarrow I\) là tăm mặt cầu ngoại tiếp tam giác \(ABC\)

Xét tam giác vuông \(AHI\) có

\(AH = \sqrt {A{I^2} - I{H^2}}  = \sqrt {A{I^2} - {{\left( {\dfrac{{SA}}{2}} \right)}^2}}  = \dfrac{a}{{\sqrt 2 }} = R\)

Ta có

\(\begin{array}{l}{S_{\Delta ABC}} = \dfrac{1}{2}AB.AC.\sin {45^0} = \dfrac{{AB.AC.BC}}{{4R}}\\ \Rightarrow BC = 2R.\sin {45^0} = \dfrac{{2a}}{{\sqrt 2 }}.\dfrac{1}{{\sqrt 2 }} = a\end{array}\)

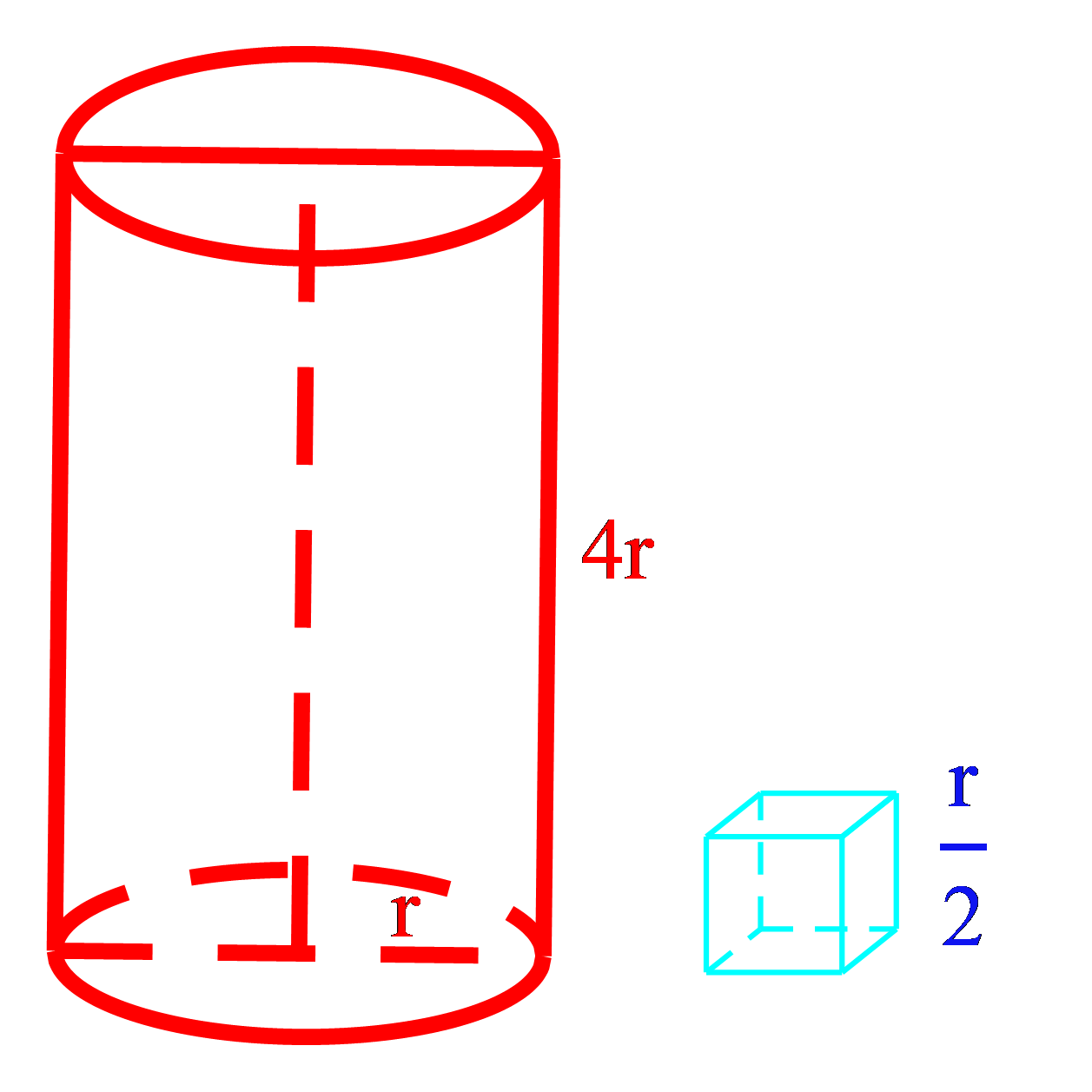
Bước 1: Gọi bán kính đáy li là \(r(r > 0)\). Tính thể tích của li theo r và thể tích của viên đá theo thể tích li.

Gọi bán kính đáy li là \(r(r > 0)\).

Khi đó, chiều cao của li là \(h = 4r;\) cạnh của viên đá là \(\dfrac{r}{2}\)

\( \Rightarrow \)Thể tích của li là \({V_0} = \pi {r^2}h = 4\pi {r^3}\).

Thể tích của một viên đá là \({V_1} = {\left( {\dfrac{r}{2}} \right)^3} = \dfrac{{{r^3}}}{8} = \dfrac{{{V_0}}}{{32\pi }}\).

Bước 2: Tính thể tích các viên đá để làm được 7 ly sinh tố

Để làm được 7 ly sinh tố cần \(7 \times 3 = 21\) viên đá.

Khi đó, thể tích các viên đá bằng \(21{V_1} = \dfrac{{21{V_0}}}{{32\pi }}\).

Bước 3: Tính thể tích sinh tố được làm từ n quả bơ

Vì mỗi quả bơ có thể làm được 2 ly sinh tố (không chứa đá) có thể tích bằng \(\dfrac{6}{7}\) thể tích li nên thể tích sinh tố bơ được làm từ một quả bơ là \(V = 2 \cdot \dfrac{6}{7}{V_0} = \dfrac{{12}}{7}{V_0}\).

\( \Rightarrow \) Thể tích sinh tố bơ được làm từ \(n\) quả bơ là \({V_n} = \dfrac{{12}}{7}n{V_0}\left( {n \in {\mathbb{N}^*}} \right)\).

Bước 4: Lập bất phương trình. Tìm n.

Tổng thể tích bơ và đá để làm 7 ly sinh tố là \(7 \cdot \dfrac{6}{7}{V_0} = 6{V_0}\).

Theo đề bài ra ta có \(\dfrac{{12}}{7}n{V_0} + \dfrac{{21{V_0}}}{{32\pi }} \ge 6{V_0} \Leftrightarrow n \ge 3,38\).

Vậy cần tối thiểu 4 quả bơ để làm được 7 ly sinh tố như yêu cầu.