Câu hỏi:
2 năm trước
Cho hình lăng trụ đứng $ABC.A’B’C’$ có đáy $ABC$ là tam giác vuông tại $A,$ \(AB = a\sqrt 3 ,\,\,BC = 2a\), đường thẳng $AC’$ tạo với mặt phẳng $(BCC’B’)$ một góc $30^0$. Diện tích mặt cầu ngoại tiếp lăng trụ đã cho bằng:
Trả lời bởi giáo viên
Đáp án đúng: b
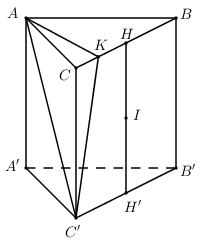
Gọi $H, H’ $ lần lượt là trung điểm của $BC$ và $B’C’$ \( \Rightarrow HH' \bot \left( {ABC} \right)\) và \(HH' \bot \left( {A'B'C'} \right)\).
Gọi $I$ là trung điểm của $HH’.$
Mặt khác \(\Delta ABC\) vuông tại $A,$ \(I \in HH' \Rightarrow \left\{ \begin{array}{l}IA = IB = IC\\IA' = IB' = IC'\end{array} \right.\)
Dễ dàng chứng minh được \(\Delta BHI = \Delta B'H'I\,\,\left( {c.g.c} \right) \Rightarrow IB = IB'\)
\( \Rightarrow IA = IB = IC = IA' = IB' = IC'\) hay $I$ là tâm mặt cầu ngoại tiếp lăng trụ $ABC.A’B’C’.$
Kẻ \(AK \bot BC\) ta có \(AK \bot \left( {BCC'B'} \right) \Rightarrow \widehat {\left( {AC';\left( {BCC'B'} \right)} \right)} = \widehat {\left( {AC';KC'} \right)} = \widehat {AC'K} = {30^0}\).
Có $AC = A'C' = \sqrt {4{a^2} - 3{a^2}} = a$
Ta có \(AK = \dfrac{{AC.AB}}{{BC}} = \dfrac{{a.a\sqrt 3 }}{{2a}} = \dfrac{{a\sqrt 3 }}{2}\)
\(\begin{array}{l} \Rightarrow AC' = \dfrac{{AK}}{{\sin 30}} = a\sqrt 3 \\ \Rightarrow AA' = \sqrt {AC{'^2} - A'C{'^2}} = \sqrt {3{a^2} - {a^2}} = a\sqrt 2 = HH'\\ \Rightarrow HI = \dfrac{1}{2}HH' = \dfrac{a}{{\sqrt 2 }} \Rightarrow BI = \sqrt {{a^2} + \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 6 }}{2} = R\\ \Rightarrow {S_{mat\,cau}} = 4\pi {\left( {\dfrac{{a\sqrt 6 }}{2}} \right)^2} = 6\pi {a^2}\end{array}\)
Hướng dẫn giải:
Diện tích mặt cầu bán kính R: \(S = 4\pi {R^2}\).
