Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật \(ABCD\) có \(AB\) và \(CD\) thuộc hai đáy của hình trụ, \(AB = 4a\),\(AC = 5a\). Thể tích khối trụ là
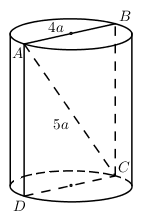
Ta có: \(BC = \sqrt {A{C^2} - A{B^2}} = \sqrt {25{a^2} - 16{a^2}} = 3a\) (Định lí Pytago)
Do đó khối trụ có bán kính đáy \(r = \dfrac{{AB}}{2} = 2a\), chiều cao \(h = AC = 3a\).
\( \Rightarrow {V_{tru}} = \pi .{r^2}h = \pi {\left( {2a} \right)^2}.3a = 12\pi {a^3}\).
Người ta thiết kế một lọ sản phẩm đựng kem chống nắng với thiết kế là một khối cầu như một viên bi khổng lồ, một nửa là nắp hộp, nửa còn lại thiết kế bên trong là một khối trụ nằm nội tiếp nửa mặt cầu để đựng kem chống nắng. Theo dự kiến nhà sản xuất dự định để khối cầu có bán kính \(R = 3\sqrt 2 a\). Để đựng được nhiều kem nhất thì chiều cao của khối trụ là \(h = m\sqrt n a\) với \(m,n \in \mathbb{N}\). Mệnh đề nào sau đây đúng?
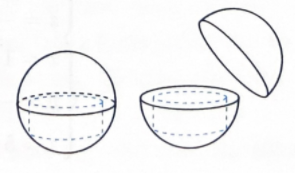
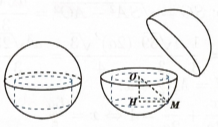
Giả sử chiều cao của khối trụ là \(OH = h(0 \le h \le 3\sqrt 2 a)\).
Ta có \(OM = R = 3\sqrt 2 a,HM = \sqrt {18{a^2} - {h^2}} \).
Vậy \({V_{{\rm{tr }}}} = \pi {\left( {\sqrt {18{a^2} - {h^2}} } \right)^2}.h = \pi \left( {18{a^2} - {h^2}} \right).h\).
Xét hàm số \(y = \pi \left( {18{a^2} - {h^2}} \right)h\) trên đoạn \([0;3\sqrt 2 a]\)
\( \Rightarrow {y^\prime } = \pi \left( {18{a^2} - 3{h^2}} \right)\)
\( \Rightarrow {y^\prime } = 0 \Leftrightarrow h = \sqrt 6 a\).
Ta có \(y(\sqrt 6 a) = 12\sqrt 6 {a^3}\pi ,\)\(y(0) = 0,\)\(y(3\sqrt 2 a) = 0\).
Vậy \({V_{{\rm{tr }}}}\) lớn nhất khi \(h = \sqrt 6 a\)=> m=1; n=6
\( \Rightarrow m + n = 1 + 6 = 7\).
Cho hình trụ có bán kính đáy \(r\) và độ dài đường sinh \(l\). Diện tích xung quanh \({S_{xq}}\) của hình trụ đã cho được tính theo công thức nào dưới đây?
Công thức tính diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi rl\)
Đề chính thức ĐGNL HCM 2019
Một miếng tôn hình chữ nhật có chiều dài $98cm$, chiều rộng $30 cm$ được uốn lại thành mặt xung quanh của một thùng chứa nước. Biết rằng chỗ mối ghép mất $2 cm$, hỏi thùng đó chứa được số lít nước xấp xỉ bằng bao nhiêu ?
Vì chỗ ghép mất 2cm nên chu vi đáy của chiếc thùng là 98-2=96(cm)
Gọi $r$ là bán kính đáy, khi đó:
\(2\pi r = 96 \Rightarrow r = \dfrac{{48}}{\pi }\left( {cm} \right)\)
Thể tích của chiếc thùng là: \(V = \pi {r^2}h = \pi .{\left( {\dfrac{{48}}{\pi }} \right)^2}.30 = \dfrac{{69120}}{\pi }\) \( \approx 22002c{m^3} \approx 22d{m^3} \approx 22\) (lít)
Cho hình trụ có diện tích xung quanh \({S_{xq}}\) và bán kính đáy \(r\). Công thức tính chiều cao hình trụ là:
Ta có: \({S_{xq}} = 2\pi rh \Leftrightarrow h = \dfrac{{{S_{xq}}}}{{2\pi r}}\)
Công thức nào sau đây không đúng khi tính diện tích toàn phần hình trụ?
Ta có: \({S_{tp}} = {S_{xq}} + 2{S_d} = 2\pi rh + 2\pi {r^2} = 2\pi r\left( {h + r} \right) = {C_d}.\left( {h + r} \right)\)
Dó đó công thức ở đáp án D là sai.
Chiều cao khối trụ có thể tích \(V\) và diện tích đáy \({S_d}\) là:
Ta có: \(V = \pi {r^2}h = {S_d}.h \Rightarrow h = \dfrac{V}{{{S_d}}}\)
Đề thi THPT QG - 2021 - mã 103
Cho khối trụ có bán kính đáy \(r = 2\) và chiều cao \(h = 3\). Thể tích của khối trụ đã cho bằng:
\(V = \pi {r^2}h = \pi {.2^2}.3 = 12\pi \).
Có một miếng bìa hình chữ nhật \(ABCD\) với \(AB = 3\) và \(AD = 6\). Trên cạnh \(AD\) lấy điểm \(E\) sao cho \(AE = 2\), trên cạnh \(BC\) lấy điểm \(F\) là trung điểm của \(BC\). Cuốn miếng bìa lại sao cho \(AB\) trùng \(DC\)để tạo thành mặt xung quanh của một hình trụ.
Khi đó tính thể tích \(V\) của tứ diện \(ABEF\).
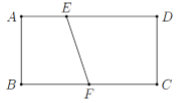
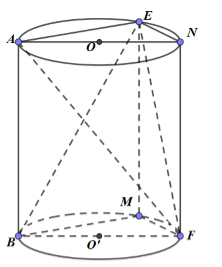
Dựng hình lăng trụ (như hình vẽ).
\(\begin{array}{l}{V_{ABEF}} = \dfrac{1}{2}{V_{F.AEMB}} = \dfrac{1}{2}\left( {{V_{AEN.BMF}} - {V_{F.AEN}}} \right) = \dfrac{1}{2}.\left( {{V_{AEN.BMF}} - \dfrac{1}{3}{V_{AEN.BMF}}} \right)\\ = \dfrac{1}{2}.\dfrac{2}{3}{V_{AEN.BMF}} = \dfrac{1}{3}{V_{AEN.BMF}}\end{array}\)
\(\Delta AEN\) vuông tại E có \(AN = 2R = \dfrac{{AD}}{\pi } = \dfrac{6}{\pi }\)
Số đo góc \(\widehat {ANE} = \dfrac{1}{2}.\dfrac{1}{3}{.360^0} = {60^0}\) (do )
\( \Rightarrow \Delta AEN\) là một nửa tam giác đều cạnh \(\dfrac{6}{\pi } \Rightarrow {S_{\Delta AEN}} = \dfrac{1}{2}.\dfrac{{{{\left( {\dfrac{6}{\pi }} \right)}^2}\sqrt 3 }}{4} = \dfrac{{9\sqrt 3 }}{{2{\pi ^2}}}\)
\( \Rightarrow {V_{AEN.BMF}} = 3.\dfrac{{9\sqrt 3 }}{{2{\pi ^2}}} = \dfrac{{27\sqrt 3 }}{{2{\pi ^2}}} \Rightarrow {V_{ABEF}} = \dfrac{{9\sqrt 3 }}{{2{\pi ^2}}}\).
Đề thi THPT QG 2019 – mã đề 104
Một cơ sở sản xuất có hai bể nước hình trụ có chiều cao bằng nhau, bán kính đáy lần lượt bằng \(1m\) và \(1,5m.\) Chủ cơ sở dự định làm một bể nước mới, hình trụ, có cùng chiều cao và có thể tích bằng tổng thể tích của hai bể nước trên. Bán kính đáy của bể nước dự định làm gần nhất với kết quả nào dưới đây ?
Gọi chiều cao của bể nước là \(h\,\,\left( m \right)\,\,\left( {h > 0} \right)\).
Thể tích 2 bể nước là: \(V = \pi {.1^2}.h + \pi .1,{5^2}.h = 3,25\pi h\,\,\left( {{m^3}} \right)\).
Gọi bán kính bể nước mới là \(r\,\,\left( m \right)\,\,\left( {r > 0} \right)\).
Thể tích của 1 bế nước mới là \(V' = \pi .{r^2}h\).
Vì bể nước mới có thể tích bằng tổng thể tích của hai bể nước trên nên \(V = V'\).
\( \Leftrightarrow 3,25\pi h = \pi {r^2}h \Leftrightarrow {r^2} = 3,25 \Leftrightarrow r \approx 1,8\,\,\left( m \right)\).
Cho hình trụ có bán kính đáy \(r = 2\) và chiều cao \(h = 3\). Diện tích xung quanh của hình trụ này bằng
Diện tích xung quanh của hình trụ này bằng \({S_{xq}} = 2\pi rh = 2\pi .2.3 = 12\pi \).
Thiết diện đi qua trục của một hình trụ là một hình vuông có độ dài cạnh bằng \(a\). Tính thể tích khối trụ đó.
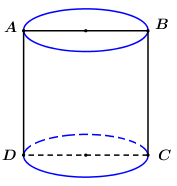
Giả sử thiết diện qua trục của hình trụ là hình vuông \(ABCD\) như hình vẽ, khi đó khối trụ đã cho có chiều cao \(h = AD = a\), bán kính đáy \(r = \dfrac{1}{2}AB = \dfrac{a}{2}\).
Khi đó thể tích khối trụ là \(V = \pi {r^2}h = \pi {\left( {\dfrac{a}{2}} \right)^2}.a = \dfrac{{\pi {a^3}}}{4}.\)
Đề thi THPT QG 2019 – mã đề 104
Cho hình trụ có chiều cao bằng \(3\sqrt 3 \). Cắt hình trụ đã cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng \(1\), thiết diện thu được có diện tích bằng \(18\). Diện tích xung quanh của hình trụ đã cho bằng
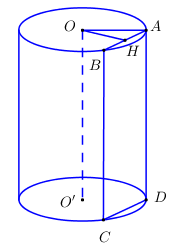
Giả sử cắt hình trụ đã cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng \(1\), ta được thiết diện là hình chữ nhật \(ABCD\) như hình vẽ.
Gọi \(H\) là trung điểm của \(AB\) ta có \(\left\{ \begin{array}{l}OH \bot AB\\OH \bot AD\,\,\left( {AD \bot day} \right)\end{array} \right. \Rightarrow OH \bot \left( {ABCD} \right) \Rightarrow OH = 1\).
Hình trụ có chiều cao bằng \(3\sqrt 3 \) (gt) \( \Rightarrow BC = AD = 3\sqrt 3 \). Mà \({S_{ABCD}} = 18\,\,\left( {gt} \right)\).
\( \Rightarrow AB.AD = 18 \Leftrightarrow AB.3\sqrt 3 = 18 \Leftrightarrow AB = 2\sqrt 3 \Rightarrow AH = \sqrt 3 \).
Áp dụng định lí Pytago trong tam giác vuông \(OAH\) ta có \(OA = \sqrt {O{H^2} + A{H^2}} = \sqrt {{1^2} + {{\left( {\sqrt 3 } \right)}^2}} = 2 = r\).
Vậy diện tích xung quanh của hình trụ đã cho là: \({S_{xq}} = 2\pi rh = 2\pi .2.3\sqrt 3 = 12\sqrt 3 \pi \).
Cắt hình trụ bởi mặt phẳng \(\left( \alpha \right)\) vuông góc với mặt đáy, ta được thiết diện là hình vuông có diện tích bằng 16. Khoảng cách từ tâm đường tròn đáy của hình trụ đến mặt phẳng \(\left( \alpha \right)\) bằng 3. Thể tích khối trụ bằng:
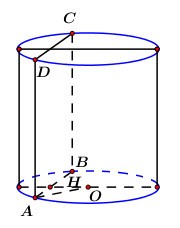
Ta có \(ABCD\) là hình vuông \( \Rightarrow {S_{ABCD}} = A{B^2} = 16\) \( \Rightarrow AB = AD = 4\)
Gọi \(H\) là trung điểm của \(AB \Rightarrow OH \bot AB\)
Lại có: \(\left( {ABCD} \right)\) vuông góc với mặt phẳng đáy \( \Rightarrow OH \bot AD\)
\( \Rightarrow OH \bot \left( {ABCD} \right)\) \( \Rightarrow d\left( {O;\,\,\left( {ABCD} \right)} \right) = OH = 3\)
Áp dụng định lý Pitago cho \(\Delta OAH\) vuông tại \(H\) ta có:
\(OA = \sqrt {O{H^2} + {{\left( {\dfrac{{AB}}{2}} \right)}^2}} = \sqrt {{3^2} + {2^2}} = \sqrt {13} \)
Khi đó ta có thể tích của hình trụ đã cho là: \(V = \pi {R^2}h = \pi .O{A^2}.AD = \pi .13.4 = 52\pi .\)
Tính diện tích toàn phần \({S_{tp}}\) của hình trụ tạo thành khi quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\), biết \(AB = 5\), \(BC = 2\).
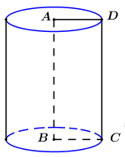
Quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) ta thu được khối trụ có chiều cao \(h = AB = 5\), bán kính đáy \(r = BC = 2\).
Vậy diện tích toàn phần của hình trụ là \(V = \pi {r^2}h + 2\pi {r^2} = \pi {.2^2}.5 + 2\pi {.2^2} = 28\pi \).
Tính diện tích toàn phần \({S_{tp}}\) của hình trụ tạo thành khi quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\), biết \(AB = 5\), \(BC = 2\).
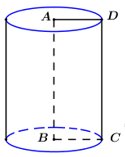
Quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) ta thu được khối trụ có chiều cao \(h = AB = 5\), bán kính đáy \(r = BC = 2\).
Vậy diện tích toàn phần của hình trụ là \(V = \pi {r^2}h + 2\pi {r^2} = \pi {.2^2}.5 + 2\pi {.2^2} = 28\pi \).
Cho hình trụ có chiều cao bằng \(5a\), cắt hình trụ bởi mặt phẳng song song với trục và cách trục một khoảng bằng \(3a\) được thiết diện có diện tích bằng \(20{a^2}\). Thể tích khối trụ là:
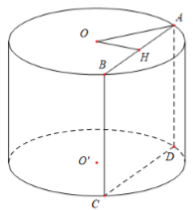
Giả sử thiết diện là hình chữ nhật \(ABCD\).
Ta có: \({S_{ABCD}} = AB.BC \Rightarrow 20{a^2} = AB.5a \Leftrightarrow AB = 4a\) \( \Rightarrow AH = 2a\).
Gọi \(O,\,\,O'\) lần lượt là tâm hai đáy của hình trụ, \(H\) là trung điểm của \(AB\).
Ta có \(\left\{ \begin{array}{l}OH \bot AB\\OH \bot BC\end{array} \right. \Rightarrow OH \bot \left( {ABCD} \right) \Rightarrow OH = 3a\).
Áp dụng định lí Pytago trong tam giác vuông \(OAH\) ta có: \(OA = \sqrt {O{H^2} + A{H^2}} = \sqrt {9{a^2} + 4{a^2}} = a\sqrt {13} \).
Vậy thể tích khối trụ là \(V = \pi .O{A^2}.BC = \pi .{\left( {a\sqrt {13} } \right)^2}.5a = 65\pi {a^3}\).
Một hình trụ có độ dài đường sinh bằng \(l\) và bán kính đường tròn đáy bằng \(R.\) Diện tích toàn phần của hình trụ đó bằng:
Diện tích toàn phần của hình trụ đã cho là: \({S_{tp}} = 2\pi Rl + 2\pi {R^2} = 2\pi R\left( {R + l} \right).\)
Tính diện tích toàn phần của hình trụ có đường cao bằng 2 và đường kính đáy bằng 8.
Bán kính đáy của hình trụ đã cho là:\(r = \frac{d}{2} = \frac{8}{2} = 4.\)
Diện tích toàn phần của hình trụ đã cho là:\({S_{tp}} = 2\pi rh + 2\pi {r^2}\) \( = 2\pi .2.4 + 2\pi {.4^2} = 48\pi .\)
Cho hình trụ có bán kính đáy bằng \(a\) và chiều cao bằng \(2a.\) Diện tích toàn phần của hình trụ bằng:
Diện tích toàn phần của hình trụ có bán kính đáy bằng \(a\) và chiếu cao bằng \(2a\) là:
\({S_{tp}} = 2\pi rh + 2\pi {r^2}\) \( = 2\pi .a.2a + 2\pi .{a^2} = 6\pi {a^2}.\)

