Câu hỏi:
2 năm trước
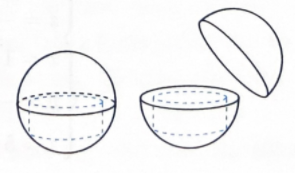
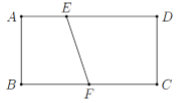
Có một miếng bìa hình chữ nhật \(ABCD\) với \(AB = 3\) và \(AD = 6\). Trên cạnh \(AD\) lấy điểm \(E\) sao cho \(AE = 2\), trên cạnh \(BC\) lấy điểm \(F\) là trung điểm của \(BC\). Cuốn miếng bìa lại sao cho \(AB\) trùng \(DC\)để tạo thành mặt xung quanh của một hình trụ.
Khi đó tính thể tích \(V\) của tứ diện \(ABEF\).
Trả lời bởi giáo viên
Đáp án đúng: b
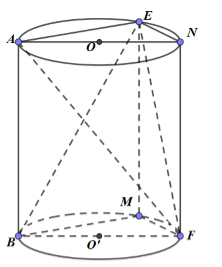
Dựng hình lăng trụ (như hình vẽ).
\(\begin{array}{l}{V_{ABEF}} = \dfrac{1}{2}{V_{F.AEMB}} = \dfrac{1}{2}\left( {{V_{AEN.BMF}} - {V_{F.AEN}}} \right) = \dfrac{1}{2}.\left( {{V_{AEN.BMF}} - \dfrac{1}{3}{V_{AEN.BMF}}} \right)\\ = \dfrac{1}{2}.\dfrac{2}{3}{V_{AEN.BMF}} = \dfrac{1}{3}{V_{AEN.BMF}}\end{array}\)
\(\Delta AEN\) vuông tại E có \(AN = 2R = \dfrac{{AD}}{\pi } = \dfrac{6}{\pi }\)
Số đo góc \(\widehat {ANE} = \dfrac{1}{2}.\dfrac{1}{3}{.360^0} = {60^0}\) (do )
\( \Rightarrow \Delta AEN\) là một nửa tam giác đều cạnh \(\dfrac{6}{\pi } \Rightarrow {S_{\Delta AEN}} = \dfrac{1}{2}.\dfrac{{{{\left( {\dfrac{6}{\pi }} \right)}^2}\sqrt 3 }}{4} = \dfrac{{9\sqrt 3 }}{{2{\pi ^2}}}\)
\( \Rightarrow {V_{AEN.BMF}} = 3.\dfrac{{9\sqrt 3 }}{{2{\pi ^2}}} = \dfrac{{27\sqrt 3 }}{{2{\pi ^2}}} \Rightarrow {V_{ABEF}} = \dfrac{{9\sqrt 3 }}{{2{\pi ^2}}}\).
Hướng dẫn giải:
Dựng hình lăng trụ, chứa các đỉnh A, B, E, F.
Lập tỉ số thể tích khối tứ diện \(ABEF\) và khối lăng trụ đó.
