Khái niệm về mặt tròn xoay (mặt nón)

Gọi chiều cao khối nón là $h$ và bán kính đáy là $r$, theo bài ra ta có $h = r$.

$\Rightarrow V = \dfrac{1}{3}\pi {r^2}h \Leftrightarrow 9\pi  = \dfrac{1}{3}\pi .{r^2}.r$ $\Leftrightarrow {r^3} = 27 \Leftrightarrow r = 3 = h$.

Vậy khối nón có chiều cao $h = 3$.

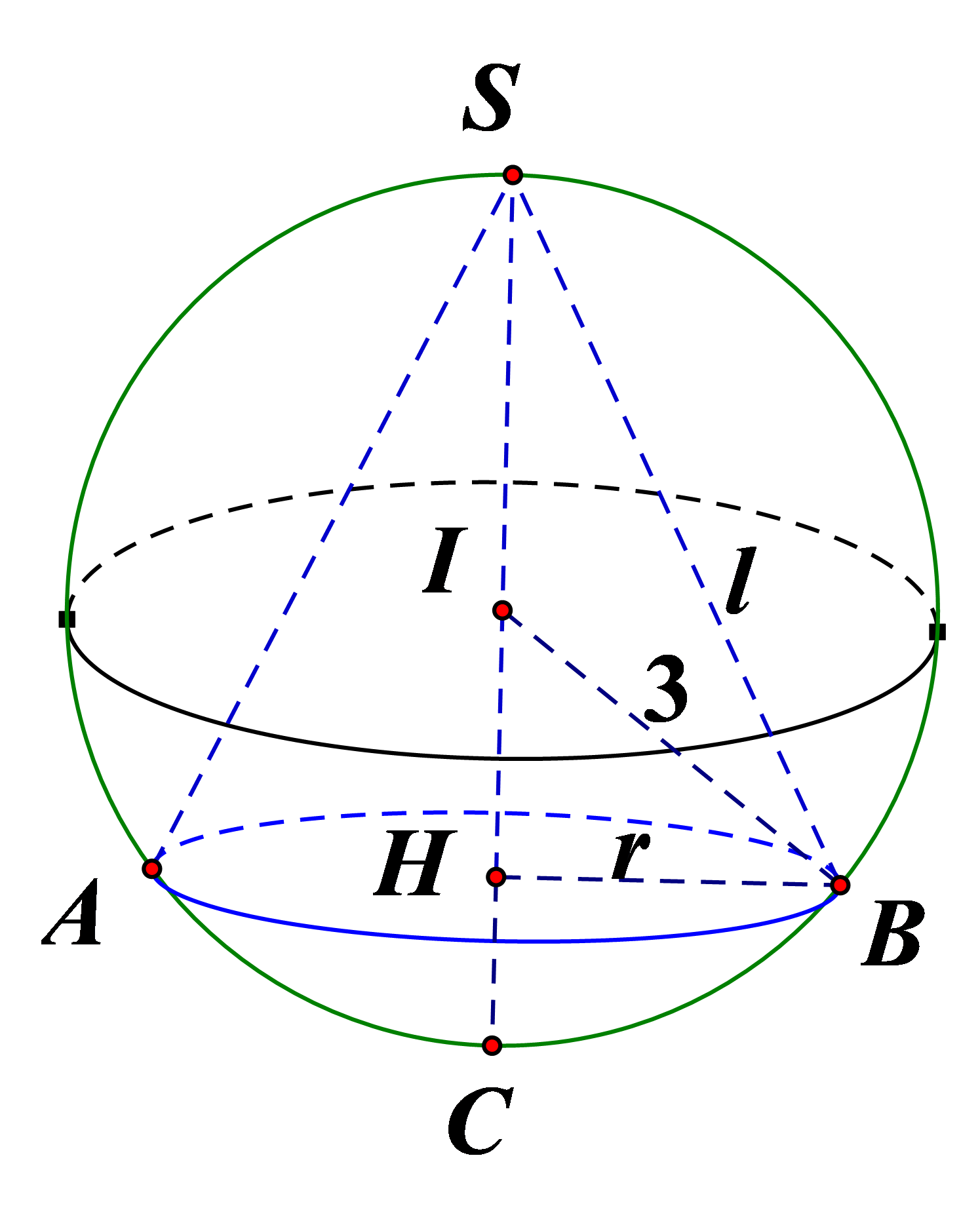
Bước 1: Tính bán kính hình cầu và biểu diễn $r$ và đường sinh $l$ theo chiều cao h của hình nón.

Vì hình cầu có thể tích bằng $36\pi$ nên bán kính hình cầu là $R = 3$.

Diện tích xung quanh của hình nón ${S_{xq}} = \pi rl$.

Gọi chiều cao của hình nón là $h$, khi đó $h \in (0;6)$.

Ta có ${r^2} = h.(2R - h) = 6h - {h^2}$, suy ra $r = \sqrt {6h - {h^2}}$.

Lại có ${l^2} = h.2R = 6h$, nên ${S_{xq}} = \pi \sqrt {6h - {h^2}}  \cdot \sqrt {6h}  = \pi \sqrt {36{h^2} - 6{h^3}}$.

Bước 2: Tìm $h$ để diện tích xung quanh lớn nhất, từ đó tìm $r$.

Ta có $36{h^2} - 6{h^3} = 3{h^2}(12 - 2h)$$= 3 \cdot h \cdot h \cdot (12 - 2h)$$\le 3 \cdot {\left( {\dfrac{{h + h + 12 - 2h}}{3}} \right)^3}$.

Hay $36{h^2} - 6{h^3} \le 192$, dấu đẳng thức xảy ra khi $h = 4$.

Khi đó $r = \sqrt {6h - {h^2}}  = 2\sqrt 2$.

Suy ra ${S_{xq}}$ lớn nhất bằng $8\sqrt 3 \pi$ khi $r = 2\sqrt 2$.

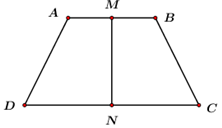
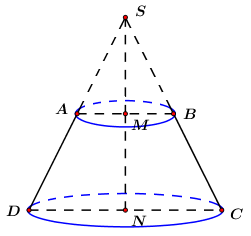
Kéo dài AD và BC cắt nhau tại S.

Quay tam giác SCD quanh trục SN được hình nón (N) đỉnh S, đáy là đường tròn đường kính CD.

Gọi hình nón đỉnh S, đáy là đường tròn đường kính AB là (M).

Theo định lý Talet ta có: $\dfrac{{SA}}{{SD}} = \dfrac{{SM}}{{SN}} = \dfrac{{AB}}{{AD}} = \dfrac{{3a}}{{6a}} = \dfrac{1}{2}$

$\Rightarrow \dfrac{{SM}}{{SN}} = \dfrac{1}{2} \Leftrightarrow \dfrac{{SM}}{{SM + 2a}} = \dfrac{1}{2}$ $\Leftrightarrow 2SM = SM + 2a$$\Leftrightarrow SM = 2a$

$\Rightarrow SN = SM + MN = 4a.$

Áp dụng định lý Pitago cho các tam giác $SAM,\,\,SDN$ vuông tại $M,\,\,N$ ta có:

$\left\{ \begin{array}{l}S{A^2} = S{M^2} + A{M^2}\\S{D^2} = S{N^2} + D{N^2}\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}S{A^2} = 4{a^2} + {\left( {\dfrac{{3a}}{2}} \right)^2} = \dfrac{{25{a^2}}}{4}\\S{D^2} = {\left( {4a} \right)^2} + {\left( {\dfrac{{6a}}{2}} \right)^2} = 25{a^2}\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}SA = \dfrac{{5a}}{2}\\SD = 5a\end{array} \right..$

$\Rightarrow$ Diện tích xung quanh hình chóp cụt cần tính là:

$\begin{array}{l}{S_{xq\,\,\left( N \right)}} - {S_{xq\,\,\left( M \right)}} = \pi .DN.SD - \pi .SA.AM\\ = \pi .5a.3a - \pi .\dfrac{{5a}}{2}.\dfrac{{3a}}{2} = \dfrac{{45\pi {a^2}}}{4} = 11,25\pi {a^2}.\end{array}$

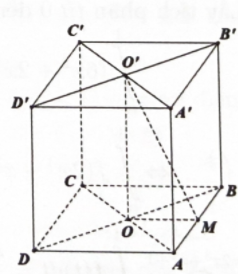
Bước 1: Gọi các điểm. Tính bán kính đáy và đường sinh của hình nón.

Giả sử ta có hình lập phương và các điểm như hình vẽ.

Bán kính đáy hình nón là $r = OM = \dfrac{1}{2}BC = \dfrac{a}{2}$.

Đường sinh hình nón là

$\begin{array}{l}1 = {O^\prime }M = \sqrt {O{O^{\prime 2}} + O{M^2}} \\ = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 5 }}{2}\end{array}$.

Bước 2: Tính diện tích toàn phần của hình nón

Diện tích toàn phần của hình nón là

${S_{tp}} = {S_{xq}} + {S_{\text{đáy}}} = \pi rl + \pi {r^2}$$= \dfrac{{\pi {a^2}(\sqrt 5  + 1)}}{4}$.

Thể tích khối nón là $V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {\left( {\sqrt 3 } \right)^2}.4 = 4\pi$.

Vì góc ở đỉnh bằng ${60^0}$ nên thiết diện qua trục là tam giác đều cạnh $2R = 2a\sqrt 2$, do đó độ dài đường sinh:

$l = 2R = 2a\sqrt 2  \Rightarrow {S_{xq}} = \pi Rl = \pi .a\sqrt 2 .2a\sqrt 2  = 4\pi {a^2}$

Diện tích đáy ${S_d} = \pi {R^2} = \pi {\left( {a\sqrt 2 } \right)^2} = 2\pi {a^2}$

Diện tích toàn phần ${S_{tp}} = {S_{xq}} + {S_d} = 4\pi {a^2} + 2\pi {a^2} = 6\pi {a^2}$

Gọi $h,\,\,l$ lần lượt là chiều cao và độ dài đường sinh của khối nón.

Khi đó:

$\begin{array}{l}{S_{xq}} = \pi rl \Leftrightarrow 12\pi  = \pi .3.l \Leftrightarrow l = 4\\ \Rightarrow h = \sqrt {{l^2} - {r^2}}  = \sqrt {{4^2} - {3^2}}  = \sqrt 7 \end{array}$

Vậy thể tích khối nón là $V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.3^2}.\sqrt 7  = 3\sqrt 7 \pi$.

Độ dài đường sinh của hình nón $l = \sqrt {{r^2} + {h^2}}  = 5a$

Diện tích xung quanh của hình nón ${S_{xq}} = \pi rl = \pi .4a.5a = 20\pi {a^2}$.

Diện tích đáy ${S_d} = \pi {r^2} = \pi {\left( {4a} \right)^2} = 16\pi {a^2}$.

Diện tích toàn phần ${S_{tp}} = {S_{xq}} + {S_d} = 20\pi {a^2} + 16\pi {a^2} = 36\pi {a^2}$

Thể tích của khối nón có chiều cao $h$ và bán kính đáy $r$ là $\dfrac{1}{3}\pi {r^2}h$.

+ ${S_{xq}} = \pi Rl \Rightarrow$ Cần tìm $R,\,\,l$.

+ Thiết diện là $\Delta SMN$ đều cạnh $4a$ $\Rightarrow l = SM = SN = 4a$.

+ $\angle \left( {\left( {SMN} \right);\left( {day} \right)} \right) = \angle SHO = {30^0}$.

Mà $SH = \dfrac{{\sqrt 3 }}{2}\left( {canh\,\,\Delta SMN} \right) = \dfrac{{\sqrt 3 }}{2}.4a = 2a\sqrt 3$.

$\Rightarrow SO = SH.\sin \angle SHO = 2\sqrt 3 a.\sin {30^0} = \sqrt 3 a$.

$\Rightarrow OM = \sqrt {S{M^2} - S{O^2}}  = \sqrt {{{\left( {4a} \right)}^2} - {{\left( {\sqrt 3 a} \right)}^2}}  = a\sqrt {13}$.

$\Rightarrow R = OM = a\sqrt {13}$.

Vậy ${S_{xq}} = \pi Rl = \pi .a\sqrt {13} .4a = 4\sqrt {13} \pi {a^2}$.

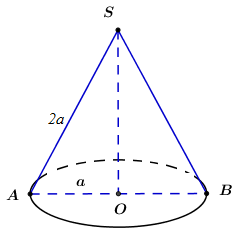
Xét $\Delta SAO$ vuông tại $O$  có: $SO = \sqrt {S{A^2} - A{O^2}}  = \sqrt {{{\left( {2a} \right)}^2} - {a^2}}  = a\sqrt 3 .$

Khi đó ta có: $V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi .{a^2}.a\sqrt 3  = \dfrac{{\pi {a^3}\sqrt 3 }}{3}.$

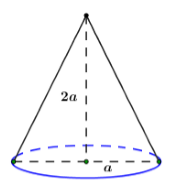
Thể tích khối nón đã cho là: $V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi .2a.{a^2} = \dfrac{{2\pi {a^3}}}{3}.$

Gọi mặt phẳng đi qua đỉnh của hình nón là $\left( {SMN} \right)$.

Do thiết diện của $\left( {SMN} \right)$ và hình nón là tam giác đều cạnh $2a$ nên $SM = MN = SN = 2a$

Kẻ $OH \bot AB$. Nối $S$ với $H.$

Khi đó $H$ là trung điểm $MN$ nên $SH = a\sqrt 3$

Ta có: góc giữa $\left( {SMN} \right)$ và mặt đáy là $\angle SHO$

Trong tam giác $SHO$ vuông tại $O$ ta có: $\tan SHO = \dfrac{{SO}}{{OH}}$$\Rightarrow \tan {30^o} = \dfrac{{SO}}{{OH}} \Rightarrow SO = \dfrac{{\sqrt 3 }}{3}.OH$

Theo định lí py-ta-go ta có: $S{O^2} + O{H^2} = S{H^2}$$\Rightarrow \dfrac{4}{3}O{H^2} = S{H^2} \Rightarrow OH = \dfrac{{\sqrt 3 }}{2}SH = \dfrac{{3a}}{2}$

$\Rightarrow SO = \dfrac{{\sqrt 3 }}{2}a$$\Rightarrow OM = \sqrt {S{M^2} - S{O^2}}  = \sqrt {4{a^2} - \dfrac{{3{a^2}}}{4}}  = \dfrac{{a\sqrt {13} }}{2}$

Diện tích xung quanh của hình nón: ${S_{xq}} = \pi .\dfrac{{a\sqrt {13} }}{2}.2a = \pi \sqrt {13} {a^2}$

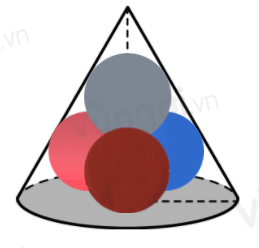
Xét trường hợp tổng quát là bốn mặt cầu có bán kính $r$.

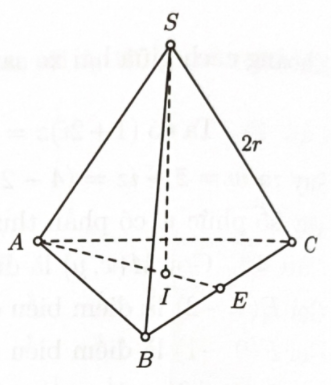
Bước 1: Gọi tâm các mặt cầu là S, A, B, C trong đó $S$ là tâm của mặt cầu trên cùng. Gọi $I$ là tâm của tam giác ABC. Tính AI và SI.

Gọi tâm các mặt cầu là S, A, B, C trong đó $S$ là tâm của mặt cầu trên cùng. Do các mặt cầu tiếp xúc ngoài nhau nên S.ABC là chóp đều cạnh 2r

Gọi $I$ là tâm của tam giác ABC, khi đó SI vuông góc với mặt phẳng $(ABC)$ và $AI = \dfrac{{2r\sqrt 3 }}{3}$.

Tam giác SAI vuông tại $I$, có

$SI = \sqrt {S{A^2} - A{I^2}}$$= \sqrt {4{r^2} - {{\left( {\dfrac{{2r\sqrt 3 }}{3}} \right)}^2}}  = \dfrac{{2r\sqrt 6 }}{3}$

Bước 2:  Kẻ đường sinh JP của hình nón tiếp xúc với hai mặt cầu tâm $S$ và tâm $A$ lần lượt tại H, K.

Ta có $\Delta SAI \backsim \Delta JSH(\;{\rm{g}} - {\rm{g}})$ nên $\dfrac{{SJ}}{{SA}} = \dfrac{{SH}}{{AI}}$

$\Rightarrow SJ = \dfrac{{SA \cdot SH}}{{AI}} = 2r \cdot r \cdot \dfrac{3}{{2r\sqrt 3 }}.$$= r\sqrt 3$

Bước 3: Biểu diễn chiều cao và bán kính của khói nón theo r

Chiều cao của khối nón là

$h = JS + SI + IO$$= r\sqrt 3  + \dfrac{{2r\sqrt 6 }}{3} + r$$= r\left( {1 + \sqrt 3  + \dfrac{{2\sqrt 6 }}{3}} \right)$

Bán kính khối nón là $R = OP = JO \cdot \tan \widehat {SJH}$

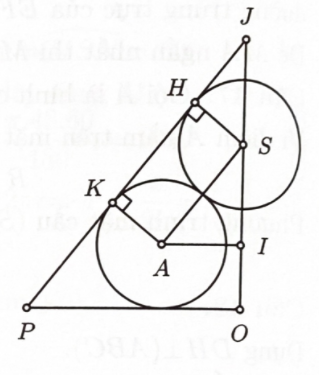
$\Leftrightarrow R = h.\tan ASI$$= r\left( {1 + \sqrt 3  + \dfrac{{2\sqrt 6 }}{3}} \right) \cdot \dfrac{{AI}}{{SI}}$$= r\left( {1 + \sqrt 3  + \dfrac{{2\sqrt 6 }}{3}} \right)\dfrac{{2r\sqrt 3 }}{3} \cdot \dfrac{3}{{2r\sqrt 6 }}$$= r\left( {1 + \sqrt 3  + \dfrac{{2\sqrt 6 }}{3}} \right)\dfrac{1}{{\sqrt 2 }}$

Bước 4: Tính R khi $r = \sqrt 2$

Áp dụng với $r = \sqrt 2$ ta được

$R = \sqrt 2  \cdot \dfrac{1}{{\sqrt 2 }} \cdot \left( {1 + \sqrt 3  + \dfrac{{2\sqrt 6 }}{3}} \right)$ $= 1 + \sqrt 3  + \dfrac{{2\sqrt 6 }}{3}$

+ Đáp án A: đúng.

+ Đáp án B: Sai vì diện tích xung quanh của hình nón tròn xoay là giới hạn của diện tích xung quanh của hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn.

+ Đáp án C: đúng.

+ Đáp án D: đúng.

Thể tích khối nón có bán kính đáy $r$ và chiều cao $h$ được tính theo công thức $V = \dfrac{1}{3}\pi {r^2}h$.

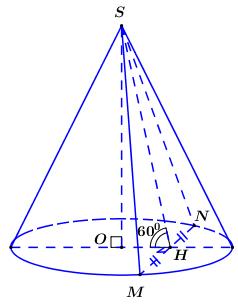
+ ${S_{xq}} = \pi Rl \Rightarrow$ Cần tìm $R,\,\,l$.

+ Thiết diện là $\Delta SMN$ đều cạnh $4a$ $\Rightarrow l = SM = SN = 4a$.

+ $\angle \left( {\left( {SMN} \right);\left( {day} \right)} \right) = \angle SHO = {60^0}$.

Mà $SH = \dfrac{{\sqrt 3 }}{2}\left( {canh\,\,\Delta SMN} \right) = \dfrac{{\sqrt 3 }}{2}.4a = 2a\sqrt 3$.

$\Rightarrow SO = SH.\sin \angle SHO = 2\sqrt 3 a.\sin {60^0} = 3a$.

$\Rightarrow OM = \sqrt {S{M^2} - S{O^2}}  = \sqrt {{{\left( {4a} \right)}^2} - {{\left( {3a} \right)}^2}}  = a\sqrt 7$.

$\Rightarrow R = OM = a\sqrt 7$.

Vậy ${S_{xq}} = \pi Rl = \pi .a\sqrt 7 .4a = 4\sqrt 7 \pi {a^2}$.

Hình nón có bán kính đáy R và chiều cao h thì đường sinh $l = \sqrt {{R^2} + {h^2}}$.

Khi đó diện tích xung quanh hình nón là ${S_{xq}} = \pi Rl = \pi R\sqrt {{R^2} + {h^2}}$.

Quay tam giác $ABC$ vuông cân tại $A$ quanh cạnh $AC$ thu được khối nón có chiều cao $h = AC = a$, bán kính đáy $r = AB = a$.

Khi đó thể tích khối nón là $V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {a^3}.$

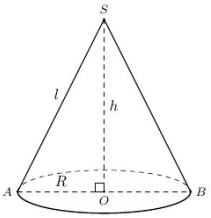
Hình nón có bán kính đáy $R,$ chiều cao $h$ và đường sinh $l$ thì ta có: ${l^2} = {h^2} + {R^2}.$

$\Rightarrow l = \sqrt {{R^2} + {h^2}} .$