Câu hỏi:
2 năm trước
Cho hình lập phương có cạnh bằng \(a\). Diện tích toàn phần của hình nón có đỉnh là tâm của một mặt còn đáy là đường tròn nội tiếp mặt đối diện là
Trả lời bởi giáo viên
Đáp án đúng: c
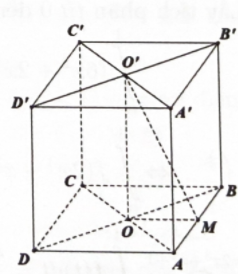
Bước 1: Gọi các điểm. Tính bán kính đáy và đường sinh của hình nón.
Giả sử ta có hình lập phương và các điểm như hình vẽ.
Bán kính đáy hình nón là \(r = OM = \dfrac{1}{2}BC = \dfrac{a}{2}\).
Đường sinh hình nón là
\(\begin{array}{l}1 = {O^\prime }M = \sqrt {O{O^{\prime 2}} + O{M^2}} \\ = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 5 }}{2}\end{array}\).
Bước 2: Tính diện tích toàn phần của hình nón
Diện tích toàn phần của hình nón là
\({S_{tp}} = {S_{xq}} + {S_{\text{đáy}}} = \pi rl + \pi {r^2}\)\( = \dfrac{{\pi {a^2}(\sqrt 5 + 1)}}{4}\).
Hướng dẫn giải:
Bước 1: Gọi các điểm. Tính bán kính đáy và đường sinh của hình nón.
Bước 2: Tính diện tích toàn phần của hình nón
