Mặt cầu ngoại tiếp, nội tiếp đa diện

Mặt cầu ngoại tiếp hình đa diện nếu nó đi qua mọi đỉnh của đa diện.

Hình chóp tứ giác đều có trục đa giác đáy chính là đường thẳng vuông góc với đáy tại tâm hình vuông.

Mọi điểm thuộc đường thẳng này đều cách đều bốn đỉnh hình vuông nên đỉnh hình chóp cũng thuộc đường thẳng này.

Do đó trục đa giác đáy của hình chóp tứ giác đều là đường thẳng đi qua đỉnh và tâm đáy.

Do $M \in \left( P \right)$ là mặt phẳng trung trực của $AB$ nên $MA = MB$.

Hình lập phương chỉ có $1$ mặt cầu ngoại tiếp là mặt cầu có tâm là tâm hình lập phương và bán kính bằng nửa độ dài đường chéo chính.

Trong các hình chóp ở mỗi đáp án đưa ra thì chỉ có hình chóp có đáy là hình chữ nhật thì luôn nội tiếp được mặt cầu.

Gọi I là trung điểm của SA.

Vì tam giác SAB vuông tại B nên IA = IB = IS

Vì tam giác SAC vuông tại C nên IA = IS = IC.

Do đó IA = IB = IC = IS nên I là tâm mặt cầu ngoại tiếp khối chóp S.ABC

Gọi D là trung điểm của BC ta có D là tâm đường tròn ngoại tiếp tam giác ABC $\Rightarrow ID \bot \left( {ABC} \right)$

$\begin{array}{*{20}{l}}{\rm{\;}}&{ \Rightarrow {V_{S.ABC}} = 2{V_{I.ABC}} = \dfrac{2}{3}ID.{S_{ABC}} \Rightarrow ID = \dfrac{{3{V_{S.ABC}}}}{{2{S_{ABC}}}} = \dfrac{{2{a^3}}}{{2{a^2}}} = a}\\{{\rm{ \;}}}&{AD = \dfrac{1}{2}BC = \dfrac{{a\sqrt 5 }}{2}}\\{{\rm{ \;}}}&{ \Rightarrow AI = \sqrt {A{D^2} + I{D^2}}  = \dfrac{{3a}}{2} = R}\end{array}$

Đường kính mặt cầu ngoại tiếp hình lập phương cạnh $a$ là $D = 2R = a\sqrt 3  = 6\sqrt 3$

Áp dụng các công thức trong tứ diện đều cạnh $a$

Bán kính mặt cầu nội tiếp $r = \dfrac{{a\sqrt 6 }}{{12}} = 2 \Rightarrow a = 4\sqrt 6$

Thể tích tứ diện đều đó là $V = \dfrac{{{a^3}\sqrt 2 }}{{12}} = \dfrac{{{{\left( {4\sqrt 6 } \right)}^3}.\sqrt 2 }}{{12}} = 64\sqrt 3$

Công thức thể khối cầu bán kính $r$ là: $V = \dfrac{4}{3}\pi {r^3}$

Bước 1: Vẽ hình minh họa cho vật thể.

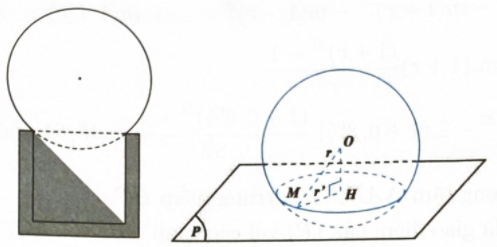
Giả sử ta có mặt cắt qua trục của vật thể như hình vẽ.

Chiều cao của hình cầu là đường kính.

=> Phần khuất cao $\dfrac{1}{6}2r = \dfrac{r}{3}$.

Bước 2: Tính khoảng cách từ tâm O đến mặt phẳng cắt và bán kính mặt trong của giá đỡ.

Suy ra $OH = \dfrac{{2r}}{3}$.

Bán kính mặt trong của giá đỡ bằng bán kính đường tròn giao tuyến.

Vậy ${r^\prime } = \sqrt {{r^2} - {{\left( {\dfrac{{2r}}{3}} \right)}^2}}  = \dfrac{{r\sqrt 5 }}{3}$.

Xét tam giác vuông $ABC$ ta có $BC = \sqrt {A{B^2} + A{C^2}}  = \sqrt {{2^2} + {4^2}}  = 2\sqrt 5$.

Tam giác $ABC$ vuông tại $A$ nên nội tiếp đường tròn đường kính $BC$.

Gọi ${R_{day}}$ là bán kính đường tròn ngoại tiếp tam giác $ABC \Rightarrow {R_{day}} = \dfrac{{BC}}{2} = \sqrt 5$.

Sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$ :

$R = \sqrt {\dfrac{{S{A^2}}}{4} + R_{day}^2}  = \sqrt {\dfrac{5}{4} + 5}  = \dfrac{5}{2}$.

Diện tích $S$ của mặt cầu bán kính $R$ là $S = 4\pi {R^2}$.

Gọi $D$ là trung điểm $A B$. Kẻ $O I$ vuông góc $S D$. Khi đó $OI \bot (SAB)$.

Suy ra $I$ là tâm của đường tròn giao tuyến của mặt cầu đã cho và $(SAB)$

Gọi $M, N$ lần lượt là giao điểm của đường tròn giao tuyến đó với $S B, S A$.

Gọi $K$ là trung điểm $MB \Rightarrow IK \bot SB$.

Đặt $AB = a > 0$. Ta có $OA = OB = OC = 1$.

Ta lại có: $OA = OB = OC = \dfrac{{a\sqrt 3 }}{3}$ nên suy ra $a = \sqrt 3$.

Ta dễ dàng tính được $SD = CD = \dfrac{3}{2},OD = \dfrac{1}{2},SO = \sqrt 2 ,OI = \dfrac{{\sqrt 2 }}{3},ID = \dfrac{1}{6}$ và SI $= \dfrac{4}{3}$.

Gọi $r$ là bán kính đường tròn giao tuyến. Khi đó $r = \sqrt {1 - O{I^2}}  = \dfrac{{\sqrt 7 }}{3}$.

Tam giác $S I K$ vuông tại $K$ và $\widehat {ISK} = {30^0 }$, suy ra $IK = \dfrac{1}{2}IS = \dfrac{2}{3}$.

Tam giác $M I K$ có $\cos I = \dfrac{{IK}}{{IM}} = \dfrac{{2\sqrt 7 }}{7}$,

Suy ra $\hat I = \arccos \dfrac{{2\sqrt 7 }}{7} = \alpha$, suy ra $\widehat {MIN} = 2\widehat {SIM} = 2\left( {\dfrac{\pi }{3} - \alpha } \right)$

Khi đó, chiều dài cung $M N$ bằng ${l_1} = 2\left( {\dfrac{\pi }{3} - \alpha } \right)\dfrac{{\sqrt 7 }}{3}$ và $l = 3{l_1} = 2\left( {\dfrac{\pi }{3} - \alpha } \right)\sqrt 7  \approx 1,77$.

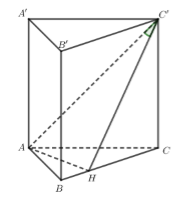
Trong mặt phẳng $\left( {ABC} \right)$ kẻ $AH \bot BC\left( {H \in BC} \right)$.

Lại có $AH \bot BB'$ (do $BB \bot \left( {ABC} \right)$ suy ra $AH \bot \left( {BCC'B'} \right)$.

Suy ra $\widehat {\left( {AC',\left( {BCC'B'} \right)} \right)} = \widehat {AC'H} = {30^0}$.

Ta có: $AC = \sqrt {B{C^2} - A{B^2}}  = a,AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{a\sqrt 3 }}{2}$

$AC' = \dfrac{{AH}}{{\sin \widehat {AC'H}}} = a\sqrt 3$ $\Rightarrow CC' = \sqrt {AC{'^2} - A{C^2}}  = a\sqrt 2$.

Gọi $R$ là bán kính mặt cầu ngoại tiếp lăng trụ, khi đó $R = \sqrt {{r^2} + \dfrac{{{h^2}}}{4}}$ với $r = \dfrac{{BC}}{2} = a$ là bán kính đường tròn ngoại tiếp tam giác vuông $ABC$ và $h = CC' = a\sqrt 2$

Do đó $R = \sqrt {{a^2} + \dfrac{{{a^2}}}{2}}  = \dfrac{{a\sqrt 6 }}{2} \Rightarrow S = 4\pi {R^2} = 4\pi .\dfrac{{6{a^2}}}{4} = 6\pi {a^2}$.

Bán kính khối cầu ngoại tiếp hình hộp: $R = \dfrac{{\sqrt {{a^2} + {b^2} + {c^2}} }}{2} = \dfrac{{\sqrt {{a^2} + 4{a^2} + 9{a^2}} }}{2} = \dfrac{{a\sqrt {14} }}{2}$.

Thể tích khối cầu: $V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi .{\left( {\dfrac{{a\sqrt {14} }}{2}} \right)^3} = \dfrac{{7\sqrt {14} \pi {a^3}}}{3}$.

Thể tích khối cầu bán kính $R = a$ là $V = \dfrac{4}{3}\pi {a^3}$

Ta có: $S = 4\pi {R^2}$

Diện tích $S$ của mặt cầu bán kính $R$ là $S = 4\pi {R^2}$.

Ta có: $S = 4\pi {R^2}$

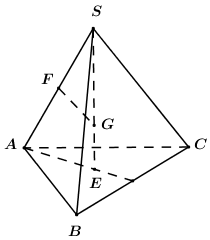
Gọi $E$ là tâm tam giác đều $ABC$ $\Rightarrow SE \bot \left( {ABC} \right)$ và $SE$ là trục của $\left( {ABC} \right)$.

Gọi $F$ là trung điểm của $SA$. Trong $\left( {SAE} \right)$, từ $F$ kẻ đường thẳng vuông góc với $SA$ và cắt $SE$ tại $G$.

Ta có: $\left\{ \begin{array}{l}G \in SE \Rightarrow GA = GB = GC\\G \in GF \Rightarrow GS = GA\end{array} \right.$ $\Rightarrow GA = GB = GC = GS$, do đó $G$ là tâm mặt cầu ngoại tiếp chóp $S.ABC$.

Xét $\Delta SFG$ và $\Delta SEA$ có: $\angle ASE$ chung, $\angle SFG = \angle SEA = {90^0}$.

$\Rightarrow \Delta SFG \sim \Delta SEA\,\,\left( {g.g} \right)$ $\Rightarrow \dfrac{{SF}}{{SE}} = \dfrac{{SG}}{{SA}}$ $\Rightarrow SG = \dfrac{{SA.SF}}{{SE}} = \dfrac{{b.\dfrac{b}{2}}}{h} = \dfrac{{{b^2}}}{{2h}}$.

Vậy bán kính mặt cầu ngoại tiếp khối chóp $S.ABC$ là $R = SG = \dfrac{{{b^2}}}{{2h}}$.