Câu hỏi:
2 năm trước
Người ta muốn làm giá đỡ cho quả cầu bằng ngọc có bán kính \(r\) sao cho phần quả cầu bị khuất chiếm \(\dfrac{1}{6}\) quả cầu theo chiều cao của nó. Biết giá đỡ hình trụ và rỗng phía trong, tính bán kính mặt trong của giá đỡ.
Trả lời bởi giáo viên
Đáp án đúng: a
Bước 1: Vẽ hình minh họa cho vật thể.
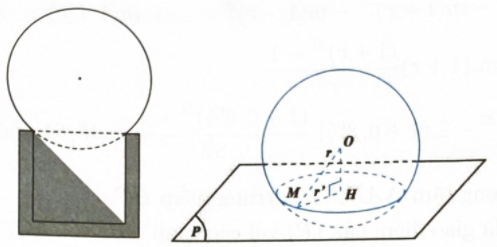
Giả sử ta có mặt cắt qua trục của vật thể như hình vẽ.
Chiều cao của hình cầu là đường kính.
=> Phần khuất cao \(\dfrac{1}{6}2r = \dfrac{r}{3}\).
Bước 2: Tính khoảng cách từ tâm O đến mặt phẳng cắt và bán kính mặt trong của giá đỡ.
Suy ra \(OH = \dfrac{{2r}}{3}\).
Bán kính mặt trong của giá đỡ bằng bán kính đường tròn giao tuyến.
Vậy \({r^\prime } = \sqrt {{r^2} - {{\left( {\dfrac{{2r}}{3}} \right)}^2}} = \dfrac{{r\sqrt 5 }}{3}\).
Hướng dẫn giải:
Bước 1: Vẽ hình minh họa cho vật thể.
Bước 2: Tính khoảng cách từ tâm O đến mặt phẳng cắt và bán kính mặt trong của giá đỡ
