Cho mặt cầu \(\left( S \right)\) tâm \(O\), bán kính \(R\) và mặt phẳng \(\left( P \right)\), gọi \(H\) là hình chiếu của \(O\) trên \(\left( P \right)\). Nếu \(R > OH\) thì:
Nếu \(OH < R\) thì \(\left( P \right)\) cắt \(\left( S \right)\) theo giao tuyến là một đường tròn.
Cho khối nón tròn xoay có đường cao $h = 15cm$ và đường sinh $l = 25cm$. Thể tích \({\rm{V}}\) của khối nón là:
Bán kính đáy của hình nón là $r = \sqrt {{l^2} - {h^2}} = \sqrt {{{25}^2} - {{15}^2}} = 20$
Thể tích khối nón là $V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}.\pi {.20^2}.15 = 2000\pi \left( {c{m^3}} \right)$
Cho mặt cầu \(\left( S \right)\). Nếu \(\left( P \right)\) là mặt phẳng kính của mặt cầu \(\left( S \right)\) thì:
Nếu \(\left( P \right)\) là mặt phẳng kính thì \(OH = 0\left( {H \equiv O} \right)\) hay \(\left( P \right)\) đi qua \(O\) là tâm mặt cầu.
Mệnh đề nào sau đây là sai?
Đáp án A: Phép vị tự tỉ số \(k\) là phép đồng dạng tỉ số \(\left| k \right|\): Đúng.
Đáp án B: Phép đồng dạng là phép biến hình: Sai vì nếu tỉ số đồng dạng khác \(1\) thì nó làm thay đổi khoảng cách giữa các điểm.
Cho mặt cầu \(\left( S \right)\) có tâm \(O\) bán kính \(R\) và đường thẳng \(d\). Nếu \(d\) và \(\left( S \right)\) không có điểm chung thì:
Mặt cầu \(\left( S \right)\) và đường thẳng \(d\) không có điểm chung nếu \(d\left( {O;d} \right) > R\).
Trong các khẳng định sau khẳng định nào sai?
Phép quay biến đưởng thẳng thành đường thẳng, biến đoạn thẳng thảnh đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó,biến đường tròn thành đường tròn có cùng bán kính với nó.
Cho một hình nón có bán kính đáy bằng \(a\) và góc ở đỉnh bằng \(60^\circ \). Tính diện tích xung quanh của hình nón đó.
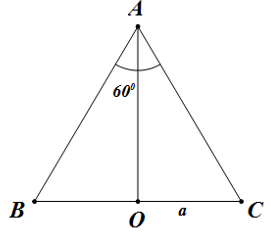
Giả sử thiết diện của mặt phẳng đi qua trục của hình nón với hình nón là tam giác \(ABC\), theo giả thiết bài toán, ta có \(ABC\) là tam giác đều cạnh \(2a\). Do đó hình nón có:
Bán kính đáy \(R = a\).
Độ dài đường sinh \(l = AC = 2a\).
Diện tích xung quanh cần tìm \({S_{xq}} = \pi Rl = \pi .a.2a = 2\pi {a^2}\).
Cho khối \(\left( N \right)\) có bán kính đáy bằng \(3\) và diện tích xung quanh bằng \(15\pi \). Tính thể tích \(V\) của khối nón \(\left( N \right)\)
Gọi \(l\) là đường sinh của hình nón, ta có \(l = \sqrt {{R^2} + {h^2}} \).
Diện tích xung quanh của hình nón là \(15\pi \), suy ra \(15\pi = \pi Rl \Leftrightarrow 15 = 3.\sqrt {{3^2} + {h^2}} \Leftrightarrow h = 4\)
Thể tích khối nón là \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {.3^2}.4 = 12\pi \) (đvtt).
Trục đa giác đáy là đường thẳng vuông góc với mặt phẳng đáy tại:
Trục đa giác đáy: là đường thẳng đi qua tâm đường tròn ngoại tiếp đa giác đáy và vuông góc với mặt phẳng chứa đa giác đáy.
Cho hình nón tròn xoay có đường cao \(h = 40cm\), bán kính đáy \(r = 50cm\). Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là \(24cm\). Tính diện tích của thiết diện.
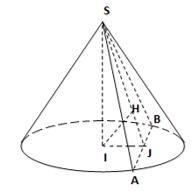
Gọi \(J\) là trung điểm của \(AB\).
Có : \(\left\{ \begin{array}{l}AB \bot IJ\\AB \bot SI\end{array} \right. \Rightarrow AB \bot \left( {SJI} \right)\)
Nên : \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {SIJ} \right)\\\left( {SAB} \right) \cap \left( {SIJ} \right) = SJ\\IH \bot SJ\end{array} \right. \Rightarrow d\left( {I,\left( {SAB} \right)} \right) = IH = 24\)
\(\dfrac{1}{{I{H^2}}} = \dfrac{1}{{S{I^2}}} + \dfrac{1}{{{\rm{I}}{{\rm{J}}^2}}} \Leftrightarrow \dfrac{1}{{{\rm{I}}{{\rm{J}}^2}}} = - \dfrac{1}{{{{40}^2}}} + \dfrac{1}{{{{24}^2}}} \Leftrightarrow JI = 30\)
Nên : \(BJ = \sqrt {{{50}^2} - {{30}^2}} = 40\)
Và \(SJ = \sqrt {{{40}^2} + {{30}^2}} = 50\)
Vậy : \({S_{\Delta SAB}} = \dfrac{1}{2}SJ.AB = \dfrac{1}{2}50.80 = 2000\left( {c{m^2}} \right).\)
Trong không gian, tập hợp các điểm cách đều hai đầu mút của đoạn thẳng là:
Mọi điểm nằm trên mặt phẳng trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng và ngược lại.
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục \(DF\)
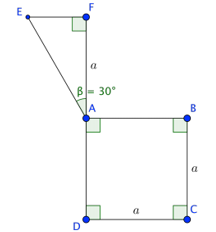
Ta có $EF = AF.\tan \beta = a.\tan 30^\circ = \dfrac{{a\sqrt 3 }}{3}$
Khi quay quanh trục \(DF\), tam giác \(AEF\) tạo ra một hình nón có thể tích
\({V_1} = \dfrac{1}{3}\pi .E{F^2}.AF = \dfrac{1}{3}\pi .{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)^2}.a = \dfrac{{\pi {a^3}}}{9}\)
Khi quay quanh trục \(DF\), hình vuông \(ABCD\) tạo ra một hình trụ có thể tích
\({V_2} = \pi .D{C^2}.BC = \pi .{a^2}.a = \pi {a^3}\)
Thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục \(DF\)là
\(V = {V_1} + {V_2} = \dfrac{{\pi {a^3}}}{9} + \pi {a^3} = \dfrac{{10}}{9}\pi {a^3}\)
Cho một khối trụ có độ dài đường sinh là $l$ và bán kính đường tròn đáy là $r$. Diện tích toàn phần của hình trụ là
\({S_{tp}} = 2{S_d}{\rm{ + }}{{\rm{S}}_{xq}} = l.2\pi r + 2\pi .{r^2} = 2\pi r\left( {l + r} \right)\)
Cho hình trụ có bán kính đáy $5{\rm{ }}cm$ chiều cao $4{\rm{ }}cm$. Diện tích toàn phần của hình trụ này là
Hình trụ có bán kính đáy \(R = 5\left( {cm} \right)\) và chiều cao \(h = 4\left( {cm} \right).\)
Diện tích toàn phần của hình trụ này là: \({S_{tp}} = 2\pi {R^2} + 2\pi Rh = 2\pi .25 + 2\pi .5.4 = 90\pi \left( {c{m^2}} \right).\)
Cho một khối trụ có chiều cao bằng \(8cm\), bán kính đường tròn đáy bằng \(6cm\). Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục \(4cm\). Diện tích của thiết diện được tạo thành là :
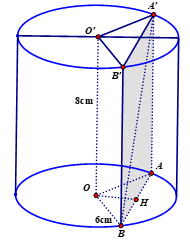
Ta có mặt phẳng \(\left( {A'AB} \right)//O'O\)
Kẻ \(A'B'//AB\) \( \Rightarrow \) thiết diện tạo thành là hình chữ nhật \(ABB'A'\)
Kẻ \(OH \bot AB,OH \bot A'A\) \( \Rightarrow OH \bot \left( {A'AB} \right)\)
\( \Rightarrow \) \(d\left( {O'O,\left( {A'AB} \right)} \right) = d\left( {O,\left( {A'ABB'} \right)} \right) \) \(= OH = 4\)
Mà \(AH = \sqrt {O{A^2} - O{H^2}} = 2\sqrt 5 \) \(\Rightarrow AB = 4\sqrt 5 \Rightarrow {S_{ABB'A'}} = 32\sqrt 5 \)
Cho hình lăng trụ đứng có đáy là tam giác với độ dài cạnh đáy lần lượt $5cm,13cm,12cm$. Một hình trụ có chiều cao bằng $8cm$ ngoại tiếp lăng trụ đã cho có thể tích bằng
Đáy là tam giác với độ dài cạnh đáy lần lượt là $5cm;12cm;13cm$ nên đáy là tam giác vuông với độ dài cạnh huyền là $13cm$. Suy ra hình trụ ngoại tiếp hình lăng trụ đứng có đáy là đường tròn bán kính là \(\dfrac{{13}}{2}cm\) .
Vậy thể tích hình trụ đó là \(V = \pi {\left( {\dfrac{{13}}{2}} \right)^2}.8 = 338\pi (cm^3) \)
Cho mặt cầu có diện tích là $72\pi \left( {c{m^2}} \right)$. Bán kính \(R\) của khối cầu là:
Có $S = 4\pi {R^2} = 72\pi \Rightarrow R = \sqrt {\dfrac{{72\pi }}{{4\pi }}} = \sqrt {18} = 3\sqrt 2 \left( {cm} \right)$
Một hình hộp chữ nhật có độ dài \(3\) cạnh lần lượt là \(2\), \(2\), \(1\). Tính bán kính \(R\) mặt cầu ngoại tiếp hình hộp nói trên.
Ta có đường chéo hình hộp \(d = \sqrt {{1^2} + {2^2} + {2^2}} = 3\).
\( \Rightarrow R = \dfrac{d}{2} = \dfrac{3}{2}\).
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a\), \(AD = 2a\) và \(AA' = 2a\). Tính bán kính \(R\) của mặt cầu ngoại tiếp tứ diện \(ABB'C'\).
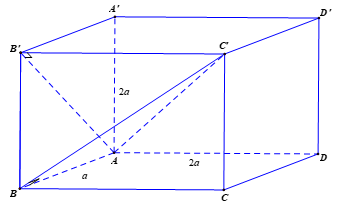
Mặt cầu ngoại tiếp tứ diện \(ABB'C'\) cũng là mặt cầu ngoại tiếp hình hộp chữ nhật \(ABCD.A'B'C'D'\)
Do đó bán kính là \(R = \dfrac{1}{2}\sqrt {{a^2} + {{\left( {2a} \right)}^2} + {{\left( {2a} \right)}^2}} = \dfrac{{3a}}{2}\).
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\); \(SA = a\) đáy \(ABC\) là tam giác vuông tại \(B\), \(\widehat {BAC} = 60^\circ \) và \(AB = \dfrac{a}{2}\). Gọi \(\left( S \right)\) là mặt cầu ngoại tiếp hình chóp \(S.ABC\). Tìm mệnh đề sai.
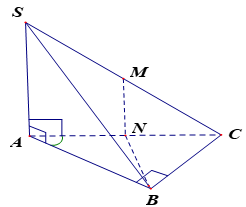
Gọi \(N,\,M\) lần lượt là trung điểm của \(AC;\,SC\).
\(ABC\) là tam giác vuông tại \(B\), \(\widehat {BAC} = {60^o}\) và \(AB = \dfrac{a}{2}\) nên \(NA = NB = NC\); \(AC = a \Rightarrow SC = a\sqrt 2 \Rightarrow MC = \dfrac{{a\sqrt 2 }}{2}\).
\(NM\) là đường trung bình của tam giác \(SAC\) nên \(NM//SA \Rightarrow NM \bot \left( {ABC} \right)\, \Rightarrow \,\,{\rm{MS = MC = MA = MB}}\)
\( \Rightarrow \) $M$ là tâm của \(\left( S \right)\) có bán kính \(MC = \dfrac{{a\sqrt 2 }}{2}\).
\( \Rightarrow {V_{{}_{\left( S \right)}}} = \dfrac{4}{3}\pi {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^3} = \dfrac{{\sqrt 2 \pi {a^3}}}{3}\).
Diện tích của \(\left( S \right):\,S = 4\pi {r^2} = 4\pi {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2} = 2\pi {a^2}.\)

