Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau
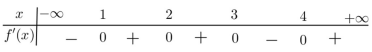
Hàm số y=3f(x+2)−x3+3x đồng biến trên khoảng nào dưới đây ?
Ta có : y=3f(x+2)−x3+3x ⇒y′=3f′(x+2)−3x2+3.
Xét −1<x<0 ta có :
{1<x+2<2⇒f′(x+2)>0x2<1⇔x2−1<0 ⇒3f′(x+2)−3x2+3>0∀x∈(−1;0).
Vậy hàm số đã cho đồng biến trên (−1;0).
Cho hàm số y=f(x) có đồ thị y=f′(x) như hình vẽ. Xét hàm số g(x)=f(x)−13x3−34x2+32x+2018. Mệnh đề nào dưới đây đúng?

Ta có: g\left( x \right) = f\left( x \right) - \dfrac{1}{3}{x^3} - \dfrac{3}{4}{x^2} + \dfrac{3}{2}x + 2018\,\,\,\,\, \Rightarrow \,\,\,\,\,g'\left( x \right) = f'\left( x \right) - {x^2} - \dfrac{3}{2}x + \dfrac{3}{2}
Căn cứ vào đồ thị y = f'\left( x \right), ta có: \left\{ \begin{array}{l}f'\left( { - 1} \right) = - 2\\f'\left( 1 \right) = 1\\f'\left( { - 3} \right) = 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}g'\left( { - 1} \right) = 0\\g'\left( 1 \right) = 0\\g'\left( { - 3} \right) = 0\end{array} \right.
Ngoài ra, vẽ đồ thị \left( P \right) của hàm số y = {x^2} + \dfrac{3}{2}x - \dfrac{3}{2} trên cùng hệ trục tọa độ như hình vẽ bên (đường nét đứt), ta thấy \left( P \right) đi qua các điểm \left( { - 3;3} \right), \left( { - 1; - 2} \right), \left( {1;1} \right) với đỉnh I\left( { - \dfrac{3}{4}; - \dfrac{{33}}{{16}}} \right). Rõ ràng
- Trên khoảng \left( { - 1;1} \right) thì f'\left( x \right) > {x^2} + \dfrac{3}{2}x - \dfrac{3}{2}, nên g'\left( x \right) > 0\;\;\forall x \in \left( { - 1;1} \right)
- Trên khoảng \left( { - 3; - 1} \right) thì f'\left( x \right) < {x^2} + \dfrac{3}{2}x - \dfrac{3}{2}, nên g'\left( x \right) < 0\;\;\forall x \in \left( { - 3; - 1} \right)
Từ những nhận định trên, ta có bảng biến thiên của hàm y = g'\left( x \right) trên \left[ { - 3;1} \right] như sau:
Vậy \mathop {\min }\limits_{\left[ { - 3;\,\,1} \right]} g\left( x \right) = g\left( { - 1} \right)
Có bao nhiêu giá trị nguyên của tham số m để đường thẳng y = m\left( {x - 4} \right) cắt đồ thị của hàm số y = \left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right) tại bốn điểm phân biệt?
Ta có phương trình hoành độ giao điểm
\left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right) = m\left( {x - 4} \right) \Rightarrow \,\,\,\,\,\dfrac{{\left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right)}}{{\left( {x - 4} \right)}} = m\,\,\,\,\left( 1 \right), \left( {x \ne 4} \right)
Số nghiệm của \left( 1 \right) bằng số giao điểm của 2 đồ thị hàm số y = f\left( x \right) = \dfrac{{\left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right)}}{{\left( {x - 4} \right)}} và y = m
Ta có: f'\left( x \right) = \dfrac{{2x\left( {{x^2} - 9} \right)\left( {x - 4} \right) + 2x\left( {{x^2} - 1} \right)\left( {x - 4} \right) - \left( {{x^2} - 9} \right)\left( {{x^2} - 1} \right)}}{{{{\left( {x - 4} \right)}^2}}} = \dfrac{{3{x^4} - 16{x^3} - 10{x^2} + 80x - 9}}{{{{\left( {x - 4} \right)}^2}}}
f'\left( x \right) = 0\,\,\,\,\, \Rightarrow \,\,\,\,\,3{x^4} - 16{x^3} - 10{x^2} + 80x - 9 = 0
Giải phương trình bằng MTBT:
- Mở chức năng Table (MODE 7)
Nhập vào máy tính hàm: f\left( x \right) = 3{x^4} - 16{x^3} - 10{x^2} + 80x - 9
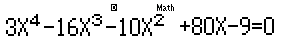
Ấn '' = '' rồi đến bước Start ấn '' - 7'', bước End ấn ''7'', bước Step ấn ''1'' rồi ấn '' = ''
Quan sát bảng và tìm các giá trị của x mà f\left( x \right) đột ngột chuyển từ âm sang dương và dương sang âm, ở đây là - 3; - 2;0;1;3;5
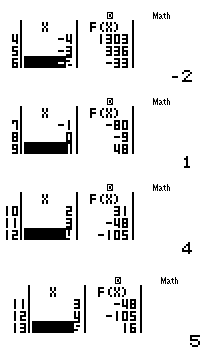
- Thoát ra ngoài (MODE 1) và nhập: 3{x^4} - 16{x^3} - 10{x^2} + 80x - 9 = 0
Sử dụng chức năng giải phương trình
+ Ấn SHIFT + SOLVE, nhập - 3 ta được một nghiệm {x_1} = - 2,1685...
+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.
+ Ấn SHIFT + SOLVE, nhập - 2 ta được một nghiệm {x_1} = - 2,1685...
+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.
+ Ấn SHIFT + SOLVE, nhập 0 ta được một nghiệm {x_2} = 0,114...
+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.
+ Ấn SHIFT + SOLVE, nhập 1 ta được một nghiệm {x_2} = 0,114...
+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.
+ Ấn SHIFT + SLOVE, nhập 3 ta được một nghiệm {x_3} = 2,447...
+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.
+ Ấn SHIFT + SOLVE, nhập 5 ta được một nghiệm {x_4} = 4,94...
Vậy ta được 4 nghiệm \left[ {\begin{array}{*{20}{c}}{{x_1} \approx - 2,169}\\{{x_2} \approx 0,114}\\{{x_3} \approx 2,45}\\{{x_4} \approx 4,94}\end{array}} \right.
Các nghiệm này đã được lưu chính xác ở trong bộ nhớ của MTBT.
Bảng biến thiên:
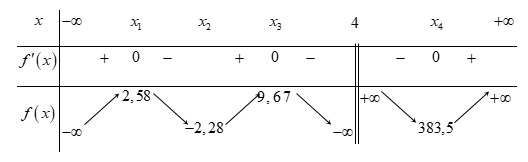
Phương trình đã cho có 4 nghiệm phân biệt \Leftrightarrow đường thẳng y = m cắt đồ thị hàm số y = f\left( x \right) = \dfrac{{\left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right)}}{{\left( {x - 4} \right)}} tại 4 điểm phân biệt
\Leftrightarrow m \in \left( { - 2,28;2,58} \right)
Mà m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2; - 1;\,\,0;\,1;\,2} \right\}.
Vậy có 5 giá trị của m thỏa bài toán.
Hàm số y = {\left( {x + m} \right)^3} + {\left( {x + n} \right)^3} - {x^3} (tham số m;n) đồng biến trên khoảng \left( { - \infty ;\, + \infty } \right). Giá trị nhỏ nhất của biểu thức P = 4\left( {{m^2} + {n^2}} \right) - m - n bằng
Ta có y' = 3{\left( {x + m} \right)^2} + 3{\left( {x + n} \right)^2} - 3{x^2} = 3\left[ {{x^2} + 2\left( {m + n} \right)x + {m^2} + {n^2}} \right]
Hàm số đồng biến trên \left( { - \infty ;\, + \infty } \right) \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta ' \le 0\end{array} \right. \Leftrightarrow mn \le 0
TH1: mn = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\n = 0\end{array} \right.
Do vai trò của m,n là như nhau nên ta chỉ cần xét trường hợp m = 0.
\Rightarrow P = 4{n^2} - n = \left( {2n - \dfrac{1}{4}} \right)^2 - \dfrac{1}{{16}} \ge - \dfrac{1}{{16}}\left( 1 \right)
TH2: m\,n < 0 \Leftrightarrow m > 0;\,n < 0 (do vai trò của m,n như nhau).
Ta có P = {\left( {2m - \dfrac{1}{4}} \right)^2} - \dfrac{1}{{16}} + 4{n^2} + \left( { - n} \right) > - \dfrac{1}{{16}}\left( 2 \right)
Từ \left( 1 \right),\left( 2 \right) ta có {P_{\min }} = - \dfrac{1}{{16}}.
Dấu "=" xảy ra khi và chỉ khi m = \dfrac{1}{8};n = 0 hoặc m = 0;n = \dfrac{1}{8}
Hình vẽ bên là đồ thị của hàm số y = f\left( x \right).
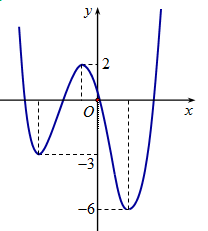
Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số y = \left| {f\left( {x - 1} \right) + m} \right| có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng
Nhận xét: Số giao điểm của \left( C \right):y = f\left( x \right) với Ox bằng số giao điểm của \left( {C'} \right):y = f\left( {x - 1} \right) với Ox (vì đồ thị hàm số \left( {C'} \right):y = f\left( {x - 1} \right) có được chỉ là do ta tịnh tiến đồ thị hàm số \left( C \right):y = f\left( x \right) sang phải 1 đơn vị)
Vì m > 0 nên \left( {C''} \right):y = f\left( {x - 1} \right) + m có được bằng cách tịnh tiến \left( {C'} \right):y = f\left( {x - 1} \right) lên trên m đơn vị.
Ta sẽ biện luận số giao điểm của y = f\left( {x - 1} \right) + m với trục Ox (cũng chính là số giao điểm của y = f\left( {x - 1} \right) với y = - m) để suy ra cực trị của hàm số y = \left| {f\left( {x - 1} \right) + m} \right|
+ TH1: - m \le - 6 \Leftrightarrow m \ge 6
Đồ thị hàm số y = \left| {f\left( {x - 1} \right) + m} \right| có dạng:
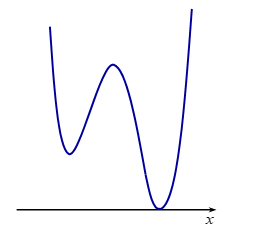
Đồ thị hàm số có 3 điểm cực trị. Loại.
+ TH2: - 6 < - m < - 3 \Leftrightarrow 3 < m < 6
Đồ thị hàm số y = \left| {f\left( {x - 1} \right) + m} \right| có dạng:
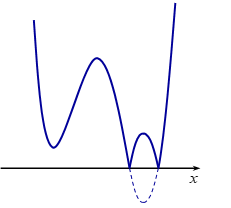
Đồ thị hàm số có 5 điểm cực trị, nhận.
+ TH3: - m = - 3 \Leftrightarrow m = 3
Đồ thị hàm số y = \left| {f\left( {x - 1} \right) + m} \right| có dạng:
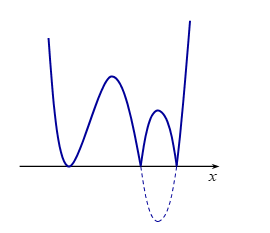
Đồ thị hàm số có 5 điểm cực trị, nhận.
+ TH4: - 3 < - m < 0 \Leftrightarrow 0 < m < 3
Đồ thị hàm số y = \left| {f\left( {x - 1} \right) + m} \right| có dạng:
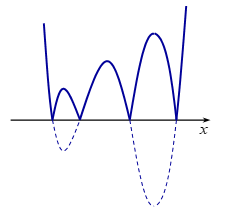
Đồ thị hàm số có 7 điểm cực trị, loại.
Vậy 3 \le m < 6. Do m \in {\mathbb{Z}^ + } nên m \in \left\{ {3;4;5} \right\}.
Vậy tổng giá trị tất cả các phần tử của S bằng 12
Tìm tất cả các giá trị thực của tham số m để hàm số y = {\sin ^3}x - 3{\cos ^2}x - m\sin x - 1 đồng biến trên đoạn \left[ {0;\dfrac{\pi }{2}} \right]
Đặt \sin x = t,x \in \left[ {0;\dfrac{\pi }{2}} \right] \Rightarrow t \in \left[ {0;1} \right]
Xét hàm số f\left( t \right) = {t^3} + 3{t^2} - mt - 4 trên [0;1]
Ta có f'\left( t \right) = 3{t^2} + 6t - m
Vì hàm số t=t(x)=\sin x đồng biến trên \left[ {0;\dfrac{\pi }{2}} \right] nên để hàm số y = {\sin ^3}x - 3{\cos ^2}x - m\sin x - 1 đồng biến trên đoạn \left[ {0;\dfrac{\pi }{2}} \right] thì hàm số f\left( t \right) phải đồng biến trên \left[ {0;1} \right] tức là:
f'\left( t \right) \ge 0,\forall t \in \left[ {0;1} \right] \Leftrightarrow 3{t^2} + 6t - m \ge 0,\forall t \in \left[ {0;1} \right] \Leftrightarrow 3{t^2} + 6t \ge m,\forall t \in \left[ {0;1} \right]
Xét hàm số g\left( t \right) = 3{t^2} + 6t trên \left[ {0;1} \right]
\begin{array}{l}g'\left( t \right) = 6t + 6\\g'\left( t \right) = 0 \Leftrightarrow t = - 1 \notin [0;1] \end{array}
Bảng biến thiên:
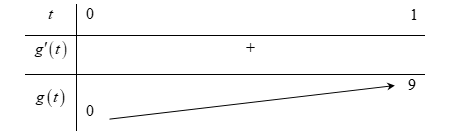
Nhìn vào bảng biến thiên ta thấy với m \le 0 thì g(t)\ge 0\ge m, \forall t\in [0;1], suy ra f'(t)\ge 0,\forall t\in [0;1] hay f(t) đồng biến trên [0;1].
Vậy với m\le 0 thì hàm số đã cho đồng biến trên đoạn \left[ {0;\dfrac{\pi }{2}} \right].
Cho hàm số y = \dfrac{{{x^3}}}{3} - a{x^2} - 3ax + 4. Để hàm số đạt cực trị tại {x_1}, {x_2} thỏa mãn \dfrac{{x_1^2 + 2a{x_2} + 9a}}{{{a^2}}} + \dfrac{{{a^2}}}{{x_2^2 + 2a{x_1} + 9a}} = 2 thì a thuộc khoảng nào ?
Đạo hàm : y' = {x^2} - 2ax - 3a, y' = 0 \Leftrightarrow {x^2} - 2ax - 3a = 0 \left( 1 \right)
Hàm số có hai cực trị {x_1},{x_2} khi y' = 0 có hai nghiệm phân biệt \Leftrightarrow \Delta ' > 0 \Leftrightarrow a < - 3 hoặc a > 0
Khi đó {x_1},{x_2} là nghiệm pt \left( 1 \right), theo định lý Viet : \left\{ \begin{array}{l}{x_1} + {x_2} = 2a\\{x_1}.{x_2} = - 3a\end{array} \right.
Do đó, thay \left\{ \begin{array}{l}2a={x_1} + {x_2} \\3a=-{x_1}.{x_2} \end{array} \right. vào đẳng thức bài cho ta được:
\left\{ \begin{array}{l}x_1^2 + 2a{x_2} + 9a = x_1^2 + \left( {{x_1} + {x_2}} \right){x_2} - 3{x_1}{x_2} = x_1^2 - 2{x_1}{x_2} + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 4{a^2} + 12a\\x_2^2 + 2a{x_1} + 9a = x_2^2 + \left( {{x_1} + {x_2}} \right){x_1} - 3{x_1}{x_2} = x_1^2 - 2{x_1}{x_2} + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 4{a^2} + 12a\end{array} \right.
Theo đề bài, ta có : \dfrac{{4a + 12}}{a} + \dfrac{a}{{4a + 12}} = 2 \Leftrightarrow \dfrac{{4a + 12}}{a} = 1 \Leftrightarrow a = - 4
Cho hàm số y = f\left( x \right) có đạo hàm trên \mathbb{R}. Đường cong trong hình vẽ bên là đồ thị hàm số y = f'\left( x \right), (y = f'\left( x \right) liên tục trên \mathbb{R}). Xét hàm số g\left( x \right) = f\left( {{x^2} - 2} \right). Mệnh đề nào dưới đây sai?
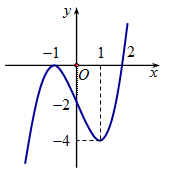
Từ đồ thị thấy f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 2\end{array} \right. và f'\left( x \right) > 0 \Leftrightarrow x > 2.
Xét g\left( x \right) = f\left( {{x^2} - 2} \right) có TXĐ D = \mathbb{R}.
g'\left( x \right) = 2xf'\left( {{x^2} - 2} \right) = 2x.f'\left( t \right) với t = {x^2} - 2
g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\t = {x^2} - 2 = - 1\\t = {x^2} - 2 = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1\\x = \pm 2\end{array} \right.
Có:
f'\left( t \right) > 0 \Leftrightarrow t = {x^2} - 2 > 2 \Leftrightarrow \left[ \begin{array}{l}x < - 2\\x > 2\end{array} \right.
f'\left( t \right) < 0 \Leftrightarrow t = {x^2} - 2 < 2 \Leftrightarrow - 2 < x < 2
Suy ra:
+) g'\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 0\\f'\left( t \right) > 0\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\f'\left( t \right) < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 0\\x < - 2;x > 2\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\ - 2 < x < 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 2\\ - 2 < x < 0\end{array} \right.
+) g'\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 0\\f'\left( t \right) < 0\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\f'\left( t \right) > 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 0\\ - 2 < x < 2\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\x > 2;x < - 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}0 < x < 2\\x < - 2\end{array} \right.
Bảng biến thiên:
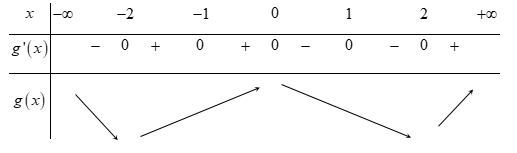
Vậy hàm số y = g\left( x \right) đồng biến trên các khoảng \left( { - 2;0} \right) và \left( {2; + \infty } \right)
Hàm số y = g\left( x \right) nghịch biến trên các khoảng \left( { - \infty ; - 2} \right) và \left( {0;2} \right)
Vậy C sai.
Cho hàm số y = \dfrac{{x + 1}}{{x - 2}}. Số các giá trị tham số m để đường thẳng y = x + m luôn cắt đồ thị hàm số tại hai điểm phân biệt A, B sao cho trọng tâm tam giác OAB nằm trên đường tròn {x^2} + {y^2} - 3y = 4 là
Phương trình hoành độ giao điểm : \dfrac{{x + 1}}{{x - 2}} = x + m \Leftrightarrow {x^2} + \left( {m - 3} \right)x - 2m - 1 = 0\left( * \right)
Theo yêu cầu bài toán : \left( * \right) phải có hai nghiệm phân biệt khác 2
\left\{ \begin{array}{l}\Delta > 0\\4 + \left( {m - 3} \right)2 - 2m - 1 \ne 0\end{array} \right. \Leftrightarrow {m^2} + 2m + 13 > 0,\forall m
Gọi A\left( {{x_1};{y_1}} \right),B\left( {{x_2};{y_2}} \right) suy ra G là trọng tâm của tam giác OAB : G\left( {\dfrac{{{x_1} + {x_2}}}{3};\dfrac{{{y_1} + {y_2}}}{3}} \right) = G\left( {\dfrac{{{x_1} + {x_2}}}{3};\dfrac{{{x_1} + {x_2} + 2m}}{3}} \right) = G\left( {\dfrac{{3 - m}}{3};\dfrac{{3 - m + 2m}}{3}} \right) = G\left( {\dfrac{{3 - m}}{3};\dfrac{{3 + m}}{3}} \right)
Theo yêu cầu bài toán : {\left( {\dfrac{{3 - m}}{3}} \right)^2} + {\left( {\dfrac{{3 + m}}{3}} \right)^2} - 3\left( {\dfrac{{3 + m}}{3}} \right) = 4 \Leftrightarrow 2{m^2} - 9m - 45 = 0 \Leftrightarrow \left[ \begin{array}{l}m = - 3\\m = \dfrac{{15}}{2}\end{array} \right.
Tìm tất cả các giá trị thực của tham số m để đường thẳng y = - 2x + m cắt đồ thị \left( H \right) của hàm số y = \dfrac{{2x + 3}}{{x + 2}} tại hai điểm A,{\rm{ }}B phân biệt sao cho P = k_1^{2018} + k_2^{2018} đạt giá trị nhỏ nhất, với {k_1},{k_2} là hệ số góc của tiếp tuyến tại A,{\rm{ }}B của đồ thị \left( H \right).
Phương trình hoành độ giao điểm \dfrac{{2x + 3}}{{x + 2}} = - 2x + m
\Leftrightarrow \left\{ \begin{array}{l}x \ne - 2\\\left( {x + 2} \right)\left( {2x - m} \right) + 2x + 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne - 2\\2{x^2} - \left( {m - 6} \right)x + 3 - 2m = 0{\rm{ (1)}}\end{array} \right.
Đường thẳng d:y = - 2x + m cắt (H) tại hai điểm phân biệt
\Leftrightarrow (1) có 2 nghiệm phân biệt khác - 2 \Leftrightarrow \left\{ \begin{array}{l}\Delta = {\left( {m - 6} \right)^2} - 8\left( {3 - 2m} \right) > 0\\2.{\left( { - 2} \right)^2} - \left( {m - 6} \right).\left( { - 2} \right) + 3 - 2m \ne 0\end{array} \right. (*)
Khi đó {x_A},{\rm{ }}{x_B} là 2 nghiệm phân biệt của (1) \Rightarrow \left\{ \begin{array}{l}{x_A} + {x_B} = \dfrac{{m - 6}}{2}\\{x_A}{x_B} = \dfrac{{3 - 2m}}{2}\end{array} \right.(2)
Ta có y' = \dfrac{1}{{{{\left( {x + 2} \right)}^2}}} \Rightarrow {k_1} = \dfrac{1}{{{{\left( {{x_A} + 2} \right)}^2}}},{\rm{ }}{k_2} = \dfrac{1}{{{{\left( {{x_B} + 2} \right)}^2}}}
\Rightarrow {k_1}{k_2} = \dfrac{1}{{{{\left[ {2\left( {{x_A} + {x_B}} \right) + {x_A}{x_B} + 4} \right]}^2}}} = \dfrac{1}{{{{\left( {m - 6 + \dfrac{{3 - 2m}}{2} + 4} \right)}^2}}} = 4
\Rightarrow P = k_1^{2018} + k_2^{2018} \ge 2\sqrt {k_1^{2018}k_2^{2018}} = 2\sqrt {{4^{2018}}} .
Dấu ''='' xảy ra \Leftrightarrow {k_1} = {k_2} > 0 \Leftrightarrow \dfrac{1}{{{{\left( {{x_A} + 2} \right)}^2}}} = \dfrac{1}{{{{\left( {{x_B} + 2} \right)}^2}}} \Leftrightarrow \left[ \begin{array}{l}{x_A} + 2 = {x_B} + 2\\{x_A} + 2 = - \left( {{x_B} + 2} \right)\end{array} \right.(3)
Do \left\{ \begin{array}{l}A \ne B\\A,{\rm{ }}B \in \left( H \right)\end{array} \right. \Rightarrow {x_A} \ne {x_B} nên (3) \Leftrightarrow {x_A} + {x_B} = - 4.
Kết hợp với (2) ta được \dfrac{{m - 6}}{2} = - 4 \Leftrightarrow m = - 2 thỏa mãn (*).
Cho hàm số y = f\left( x \right) = {x^3} + 6{x^2} + 9x + 3\,\,\left( C \right). Tồn tại hai tiếp tuyến của \left( C \right) phân biệt và có cùng hệ số góc k, đồng thời đường thẳng đi qua các tiếp điểm của hai tiếp tuyến đó cắt các trục Ox,\,\,Oy tương ứng tại A và B sao cho OA = 2017.OB. Hỏi có bao nhiêu giá trị của k thỏa mãn yêu cầu bài toán?
Gọi {M_1}\left( {{x_1};f\left( {{x_1}} \right)} \right); {M_2}\left( {{x_2};f\left( {{x_2}} \right)} \right) là hai tiếp điểm mà tại đó tiếp tuyến có cùng hệ số góc.
Ta có y' = 3{x^2} + 12x + 9
Khi đó k = 3x_1^2 + 12{x_1} + 9 = 3x_2^2 + 12{x_2} + 9 \Leftrightarrow \left( {{x_1} - {x_2}} \right)\left( {{x_1} + {x_2} + 4} \right) = 0 \Leftrightarrow {x_1} + {x_2} = - 4 = S\left( 1 \right)
Hệ số góc của đường thẳng {M_1}{M_2} là
k' = \pm \dfrac{{OB}}{{OA}} = \pm \dfrac{1}{{2017}} = \dfrac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}}
\Leftrightarrow \pm \dfrac{1}{{2017}} = {\left( {{x_1} + {x_2}} \right)^2} - {x_1}{x_2} + 6\left( {{x_1} + {x_2}} \right) + 9 \Leftrightarrow \left[ \begin{array}{l}{x_1}{x_2} = \dfrac{{2016}}{{2017}} = P\\{x_1}{x_2} = \dfrac{{2018}}{{2017}} = P\end{array} \right.\left( 2 \right)
Với \left\{ \begin{array}{l}{x_1} + {x_2} = - 4 = S\\{x_1}{x_2} = \dfrac{{2016}}{{2017}} = P\end{array} \right., do {S^2} > 4P nên \exists hai cặp {x_1},{x_2} \Rightarrow \exists 1 giá trị k
Với \left\{ \begin{array}{l}{x_1} + {x_2} = - 4 = S\\{x_1}{x_2} = \dfrac{{2018}}{{2017}} = P\end{array} \right., do {S^2} > 4P nên \exists hai cặp {x_1},{x_2} \Rightarrow \exists 1 giá trị k
KL: Có 2 giá trị k
Gọi S là tập hợp tất cả các giá trị của tham số m để bất phương trình {m^2}\left( {{x^4} - 1} \right) + m\left( {{x^2} - 1} \right) - 6\left( {x - 1} \right) \ge 0 đúng với mọi x \in R. Tổng giá trị của tất cả các phần tử thuộc S bằng:
\begin{array}{l}\;\;\;\;\;\;f\left( x \right) = {m^2}\left( {{x^4} - 1} \right) + m\left( {{x^2} - 1} \right) - 6\left( {x - 1} \right) \ge 0,\forall x\\ \Leftrightarrow {m^2}\left( {{x^2} - 1} \right)\left( {{x^2} + 1} \right) + m\left( {x - 1} \right)\left( {x + 1} \right) - 6\left( {x - 1} \right) \ge 0,\forall x\\ \Leftrightarrow \left( {x - 1} \right)\left[ {{m^2}{x^3} + {m^2}{x^2} + \left( {{m^2} + m} \right)x + {m^2} + m - 6} \right] \ge 0,\forall x\end{array}
Để bất phương trình luôn đúng với mọi x thì suy ra:
+ TH1: Phương trình {m^2}{x^3} + {m^2}{x^2} + \left( {{m^2} + m} \right)x + {m^2} + m - 6 = 0 nghiệm đúng với mọi x
\Leftrightarrow \left\{ \begin{array}{l}{m^2} = 0\\{m^2} = 0\\{m^2} + m = 0\\{m^2} + m - 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 0\\\left[ \begin{array}{l}m = 0\\m = - 1\end{array} \right.\\\left[ \begin{array}{l}m = 2\\m = - 3\end{array} \right.\end{array} \right. (vô nghiệm)
+ TH2: Đa thức {m^2}{x^3} + {m^2}{x^2} + \left( {{m^2} + m} \right)x + {m^2} + m - 6 có nghiệm x = 1
Khi đó: {m^2} + {m^2} + {m^2} + m + {m^2} + m - 6 = 0 \Leftrightarrow 4{m^2} + 2m - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - \dfrac{3}{2}\end{array} \right.
Thử lại:
+ Với m = 1 thì \left( {x - 1} \right)\left[ {{x^3} + {x^2} + 2x - 4} \right] \ge 0 \Leftrightarrow {\left( {x - 1} \right)^2}\left( {{x^2} + 2x + 4} \right) \ge 0 (luôn đúng)
+ Với m = - \dfrac{3}{2} thì \left( {x - 1} \right)\left( {\dfrac{9}{4}{x^3} + \dfrac{9}{4}{x^2} + \dfrac{3}{4}x - \dfrac{{21}}{4}} \right) \ge 0 \Leftrightarrow \left( {x - 1} \right)\left( {3{x^3} + 3{x^2} + x - 7} \right) \ge 0 \Leftrightarrow {\left( {x - 1} \right)^2}\left( {3{x^2} + 6x + 7} \right) \ge 0 (luôn đúng)
Do đó m = 1;m = - \dfrac{3}{2} là các giá trị cần tìm.
Tổng S = 1 - \dfrac{3}{2} = - \dfrac{1}{2}.
Cho hàm số f\left( x \right) = m{x^4} + n{x^3} + p{x^2} + qx + r \left( {m,n,p,q,r \in R} \right). Hàm số y = f'\left( x \right) có đồ thị như hình vẽ bên. Tập nghiệm của phương trình f\left( x \right) = r có số phần tử là
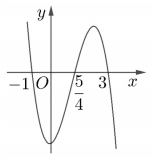
f\left( x \right) = m{x^4} + n{x^3} + p{x^2} + qx + r
Từ đồ thị hàm số y = f'\left( x \right) dễ thấy m \ne 0.
Phương trình f\left( x \right) = r \Leftrightarrow m{x^4} + n{x^3} + p{x^2} + qx = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\m{x^3} + n{x^2} + px + q = 0\,\,\left( * \right)\end{array} \right.
Xét f'\left( x \right) = 4m{x^3} + 3n{x^2} + 2px + q = 0 có ba nghiệm {x_1} = - 1;{x_2} = \dfrac{5}{4};{x_3} = 3.
Theo hệ thức Vi-et : \left\{ \begin{array}{l}{x_1} + {x_2} + {x_3} = - \dfrac{b}{a}\\{x_1}{x_2} + {x_2}{x_3} + {x_3}{x_1} = \dfrac{c}{a}\\{x_1}{x_2}{x_3} = - \dfrac{d}{a}\end{array} \right. ta có: \left\{ \begin{array}{l}\dfrac{{13}}{4} = - \dfrac{{3n}}{{4m}}\\ - \dfrac{1}{2} = \dfrac{{2p}}{{4m}}\\ - \dfrac{{15}}{4} = - \dfrac{q}{{4m}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}n = - \dfrac{{13}}{3}m\\p = - m\\q = 15m\end{array} \right.
Thay vào \left( * \right) được m{x^3} - \dfrac{{13}}{3}m{x^2} - mx + 15m = 0 \Leftrightarrow {x^3} - \dfrac{{13}}{3}{x^2} - x + 15 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{5}{3}\\x = 3\end{array} \right.
Vậy phương trình đã cho có 3 nghiệm phân biệt {x_1} = 0;\;{x_2} = 3;\;{x_3} = - \dfrac{5}{3}

