Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y = {\sin ^3}x - 3{\cos ^2}x - m\sin x - 1\) đồng biến trên đoạn \(\left[ {0;\dfrac{\pi }{2}} \right]\)
Trả lời bởi giáo viên
Đặt \(\sin x = t,x \in \left[ {0;\dfrac{\pi }{2}} \right] \Rightarrow t \in \left[ {0;1} \right]\)
Xét hàm số \(f\left( t \right) = {t^3} + 3{t^2} - mt - 4\) trên $[0;1]$
Ta có \(f'\left( t \right) = 3{t^2} + 6t - m\)
Vì hàm số $t=t(x)=\sin x$ đồng biến trên \(\left[ {0;\dfrac{\pi }{2}} \right]\) nên để hàm số \(y = {\sin ^3}x - 3{\cos ^2}x - m\sin x - 1\) đồng biến trên đoạn \(\left[ {0;\dfrac{\pi }{2}} \right]\) thì hàm số \(f\left( t \right)\) phải đồng biến trên \(\left[ {0;1} \right]\) tức là:
\(f'\left( t \right) \ge 0,\forall t \in \left[ {0;1} \right]\)\( \Leftrightarrow 3{t^2} + 6t - m \ge 0,\forall t \in \left[ {0;1} \right]\)\( \Leftrightarrow 3{t^2} + 6t \ge m,\forall t \in \left[ {0;1} \right]\)
Xét hàm số \(g\left( t \right) = 3{t^2} + 6t\) trên $\left[ {0;1} \right]$
\(\begin{array}{l}g'\left( t \right) = 6t + 6\\g'\left( t \right) = 0 \Leftrightarrow t = - 1 \notin [0;1] \end{array}\)
Bảng biến thiên:
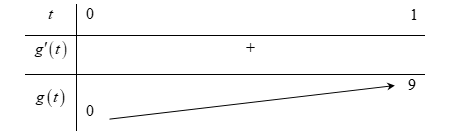
Nhìn vào bảng biến thiên ta thấy với \(m \le 0\) thì $g(t)\ge 0\ge m, \forall t\in [0;1]$, suy ra $f'(t)\ge 0,\forall t\in [0;1]$ hay $f(t)$ đồng biến trên $[0;1]$.
Vậy với $m\le 0$ thì hàm số đã cho đồng biến trên đoạn \(\left[ {0;\dfrac{\pi }{2}} \right]\).
Hướng dẫn giải:
- Đặt \(\sin x = t\), tìm điều kiện của \(t\) và đưa về hàm số bậc ba ẩn \(t\). Hàm $ f(x)$ là hàm hợp của hàm $f(t)$ và \(t=\sin x\)
- Tìm điều kiện để hàm số ẩn \(t\) đồng biến trên khoảng \(t\) đã tìm được ở trên.
Câu hỏi khác
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ. Xét hàm số \(g\left( x \right) = f\left( x \right) - \dfrac{1}{3}{x^3} - \dfrac{3}{4}{x^2} + \dfrac{3}{2}x + 2018\). Mệnh đề nào dưới đây đúng?