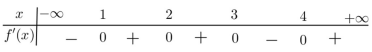Hàm số $y = {\left( {x + m} \right)^3} + {\left( {x + n} \right)^3} - {x^3}$ (tham số $m;n$) đồng biến trên khoảng $\left( { - \infty ;\, + \infty } \right)$. Giá trị nhỏ nhất của biểu thức $P = 4\left( {{m^2} + {n^2}} \right) - m - n$ bằng
Trả lời bởi giáo viên
Ta có $y' = 3{\left( {x + m} \right)^2} + 3{\left( {x + n} \right)^2} - 3{x^2} = 3\left[ {{x^2} + 2\left( {m + n} \right)x + {m^2} + {n^2}} \right]$
Hàm số đồng biến trên $\left( { - \infty ;\, + \infty } \right)$$ \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta ' \le 0\end{array} \right. \Leftrightarrow mn \le 0$
TH1: $mn = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\n = 0\end{array} \right.$
Do vai trò của $m,n$ là như nhau nên ta chỉ cần xét trường hợp $m = 0$.
$ \Rightarrow P = 4{n^2} - n = \left( {2n - \dfrac{1}{4}} \right)^2 - \dfrac{1}{{16}} \ge - \dfrac{1}{{16}}\left( 1 \right)$
TH2: $m\,n < 0 \Leftrightarrow m > 0;\,n < 0$ (do vai trò của $m,n$ như nhau).
Ta có $P = {\left( {2m - \dfrac{1}{4}} \right)^2} - \dfrac{1}{{16}} + 4{n^2} + \left( { - n} \right) > - \dfrac{1}{{16}}\left( 2 \right)$
Từ $\left( 1 \right),\left( 2 \right)$ ta có ${P_{\min }} = - \dfrac{1}{{16}}$.
Dấu "=" xảy ra khi và chỉ khi $m = \dfrac{1}{8};n = 0$ hoặc $m = 0;n = \dfrac{1}{8}$
Hướng dẫn giải:
- Hàm số đồng biến trên \(R\) \( \Leftrightarrow y' \ge 0,\forall x \in R\) suy ra điều kiện của \(m,n\)
- Dùng điều kiện của \(m,n\) tìm được ở trên để đánh giá GTNN của \(P\)
Câu hỏi khác
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ. Xét hàm số \(g\left( x \right) = f\left( x \right) - \dfrac{1}{3}{x^3} - \dfrac{3}{4}{x^2} + \dfrac{3}{2}x + 2018\). Mệnh đề nào dưới đây đúng?