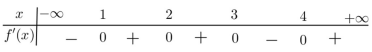Có bao nhiêu giá trị nguyên của tham số \(m\) để đường thẳng \(y = m\left( {x - 4} \right)\) cắt đồ thị của hàm số \(y = \left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right)\) tại bốn điểm phân biệt?

Ta có phương trình hoành độ giao điểm

\(\left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right) = m\left( {x - 4} \right)\) \( \Rightarrow \,\,\,\,\,\dfrac{{\left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right)}}{{\left( {x - 4} \right)}} = m\,\,\,\,\left( 1 \right)\), \(\left( {x \ne 4} \right)\)

Số nghiệm của \(\left( 1 \right)\) bằng số giao điểm của 2 đồ thị hàm số \(y = f\left( x \right) = \dfrac{{\left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right)}}{{\left( {x - 4} \right)}}\) và \(y = m\)

Ta có: \(f'\left( x \right) = \dfrac{{2x\left( {{x^2} - 9} \right)\left( {x - 4} \right) + 2x\left( {{x^2} - 1} \right)\left( {x - 4} \right) - \left( {{x^2} - 9} \right)\left( {{x^2} - 1} \right)}}{{{{\left( {x - 4} \right)}^2}}} = \dfrac{{3{x^4} - 16{x^3} - 10{x^2} + 80x - 9}}{{{{\left( {x - 4} \right)}^2}}}\)

\(f'\left( x \right) = 0\,\,\,\,\, \Rightarrow \,\,\,\,\,3{x^4} - 16{x^3} - 10{x^2} + 80x - 9 = 0\)

Giải phương trình bằng MTBT:

- Mở chức năng Table (MODE 7)

Nhập vào máy tính hàm: \(f\left( x \right) = 3{x^4} - 16{x^3} - 10{x^2} + 80x - 9\)

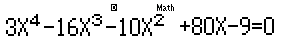
Ấn \('' = ''\) rồi đến bước Start ấn \('' - 7''\), bước End ấn \(''7''\), bước Step ấn \(''1''\) rồi ấn \('' = ''\)

Quan sát bảng và tìm các giá trị của \(x\) mà \(f\left( x \right)\) đột ngột chuyển từ âm sang dương và dương sang âm, ở đây là \( - 3; - 2;0;1;3;5\)

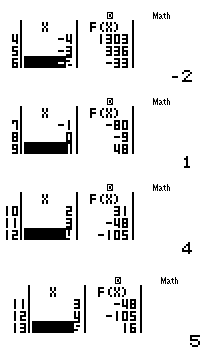
- Thoát ra ngoài (MODE 1) và nhập: \(3{x^4} - 16{x^3} - 10{x^2} + 80x - 9 = 0\)

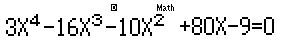
Sử dụng chức năng giải phương trình

+ Ấn SHIFT + SOLVE, nhập \( - 3\) ta được một nghiệm \({x_1} =  - 2,1685...\)

+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.

+ Ấn SHIFT + SOLVE, nhập \( - 2\) ta được một nghiệm \({x_1} =  - 2,1685...\)

+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.

+ Ấn SHIFT + SOLVE, nhập \(0\) ta được một nghiệm \({x_2} = 0,114...\)

+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.

+ Ấn SHIFT + SOLVE, nhập \(1\) ta được một nghiệm \({x_2} = 0,114...\)

+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.

+ Ấn SHIFT + SLOVE, nhập \(3\) ta được một nghiệm \({x_3} = 2,447...\)

+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.

+ Ấn SHIFT + SOLVE, nhập \(5\) ta được một nghiệm \({x_4} = 4,94...\)

 Vậy ta được $4$ nghiệm \(\left[ {\begin{array}{*{20}{c}}{{x_1} \approx  - 2,169}\\{{x_2} \approx 0,114}\\{{x_3} \approx 2,45}\\{{x_4} \approx 4,94}\end{array}} \right.\)

Các nghiệm này đã được lưu chính xác ở trong bộ nhớ của MTBT.

Bảng biến thiên:

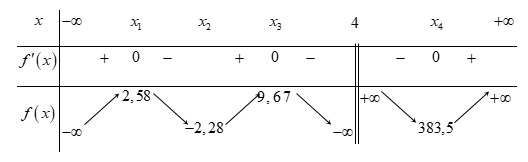
Phương trình đã cho có \(4\) nghiệm phân biệt \( \Leftrightarrow \) đường thẳng \(y = m\) cắt đồ thị hàm số         \(y = f\left( x \right) = \dfrac{{\left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right)}}{{\left( {x - 4} \right)}}\) tại \(4\) điểm phân biệt

\( \Leftrightarrow m \in \left( { - 2,28;2,58} \right)\)

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2; - 1;\,\,0;\,1;\,2} \right\}.\)

Vậy có \(5\) giá trị của \(m\) thỏa bài toán.