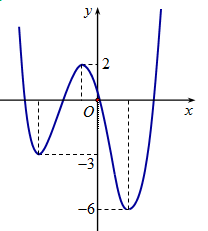
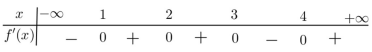Hình vẽ bên là đồ thị của hàm số $y = f\left( x \right)$.

Gọi $S$ là tập hợp các giá trị nguyên dương của tham số $m$ để hàm số $y = \left| {f\left( {x - 1} \right) + m} \right|$ có $5$ điểm cực trị. Tổng giá trị tất cả các phần tử của $S$ bằng

Nhận xét: Số giao điểm của $\left( C \right):y = f\left( x \right)$ với $Ox$ bằng số giao điểm của $\left( {C'} \right):y = f\left( {x - 1} \right)$ với $Ox$ (vì đồ thị hàm số $\left( {C'} \right):y = f\left( {x - 1} \right)$ có được chỉ là do ta tịnh tiến đồ thị hàm số $\left( C \right):y = f\left( x \right)$ sang phải \(1\) đơn vị)

Vì $m > 0$ nên $\left( {C''} \right):y = f\left( {x - 1} \right) + m$ có được bằng cách tịnh tiến $\left( {C'} \right):y = f\left( {x - 1} \right)$ lên trên $m$ đơn vị.

Ta sẽ biện luận số giao điểm của \(y = f\left( {x - 1} \right) + m\) với trục \(Ox\) (cũng chính là số giao điểm của \(y = f\left( {x - 1} \right)\) với \(y =  - m\)) để suy ra cực trị của hàm số \(y = \left| {f\left( {x - 1} \right) + m} \right|\)

+ TH1: $ - m \le  - 6 \Leftrightarrow m \ge 6$

Đồ thị hàm số \(y = \left| {f\left( {x - 1} \right) + m} \right|\) có dạng:

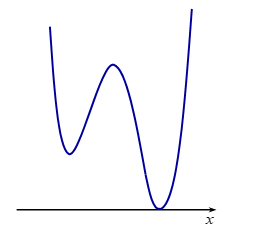
 Đồ thị hàm số có $3$ điểm cực trị. Loại.

+ TH2: \( - 6 <  - m <  - 3 \Leftrightarrow 3 < m < 6\)

Đồ thị hàm số \(y = \left| {f\left( {x - 1} \right) + m} \right|\) có dạng:

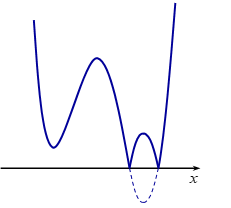
Đồ thị hàm số có \(5\) điểm cực trị, nhận.

+ TH3: \( - m =  - 3 \Leftrightarrow m = 3\)

Đồ thị hàm số \(y = \left| {f\left( {x - 1} \right) + m} \right|\) có dạng:

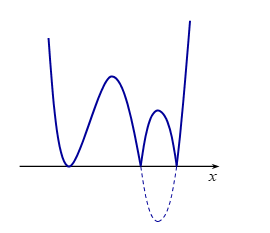
Đồ thị hàm số có \(5\) điểm cực trị, nhận.

+ TH4: \( - 3 <  - m < 0 \Leftrightarrow 0 < m < 3\)

Đồ thị hàm số \(y = \left| {f\left( {x - 1} \right) + m} \right|\) có dạng:

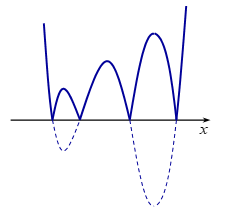
Đồ thị hàm số có \(7\) điểm cực trị, loại.

Vậy $3 \le m < 6$. Do $m \in {\mathbb{Z}^ + }$ nên $m \in \left\{ {3;4;5} \right\}$.

Vậy tổng giá trị tất cả các phần tử của $S$ bằng \(12\)