Tìm tất cả các giá trị thực của tham số \(m\) để đường thẳng $y = - 2x + m$ cắt đồ thị $\left( H \right)$ của hàm số $y = \dfrac{{2x + 3}}{{x + 2}}$ tại hai điểm \(A,{\rm{ }}B\) phân biệt sao cho \(P = k_1^{2018} + k_2^{2018}\) đạt giá trị nhỏ nhất, với \({k_1},{k_2}\) là hệ số góc của tiếp tuyến tại \(A,{\rm{ }}B\) của đồ thị $\left( H \right)$.
Trả lời bởi giáo viên
Phương trình hoành độ giao điểm $\dfrac{{2x + 3}}{{x + 2}} = - 2x + m$
$ \Leftrightarrow \left\{ \begin{array}{l}x \ne - 2\\\left( {x + 2} \right)\left( {2x - m} \right) + 2x + 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne - 2\\2{x^2} - \left( {m - 6} \right)x + 3 - 2m = 0{\rm{ (1)}}\end{array} \right.$
Đường thẳng $d:y = - 2x + m$ cắt $(H)$ tại hai điểm phân biệt
$ \Leftrightarrow $ (1) có 2 nghiệm phân biệt khác $ - 2 \Leftrightarrow \left\{ \begin{array}{l}\Delta = {\left( {m - 6} \right)^2} - 8\left( {3 - 2m} \right) > 0\\2.{\left( { - 2} \right)^2} - \left( {m - 6} \right).\left( { - 2} \right) + 3 - 2m \ne 0\end{array} \right. (*)$
Khi đó ${x_A},{\rm{ }}{x_B}$ là 2 nghiệm phân biệt của (1) $ \Rightarrow \left\{ \begin{array}{l}{x_A} + {x_B} = \dfrac{{m - 6}}{2}\\{x_A}{x_B} = \dfrac{{3 - 2m}}{2}\end{array} \right.(2)$
Ta có $y' = \dfrac{1}{{{{\left( {x + 2} \right)}^2}}} \Rightarrow {k_1} = \dfrac{1}{{{{\left( {{x_A} + 2} \right)}^2}}},{\rm{ }}{k_2} = \dfrac{1}{{{{\left( {{x_B} + 2} \right)}^2}}}$
$ \Rightarrow {k_1}{k_2} = \dfrac{1}{{{{\left[ {2\left( {{x_A} + {x_B}} \right) + {x_A}{x_B} + 4} \right]}^2}}} = \dfrac{1}{{{{\left( {m - 6 + \dfrac{{3 - 2m}}{2} + 4} \right)}^2}}} = 4$
$ \Rightarrow P = k_1^{2018} + k_2^{2018} \ge 2\sqrt {k_1^{2018}k_2^{2018}} = 2\sqrt {{4^{2018}}} .$
Dấu $''=''$ xảy ra $ \Leftrightarrow {k_1} = {k_2} > 0 \Leftrightarrow \dfrac{1}{{{{\left( {{x_A} + 2} \right)}^2}}} = \dfrac{1}{{{{\left( {{x_B} + 2} \right)}^2}}} \Leftrightarrow \left[ \begin{array}{l}{x_A} + 2 = {x_B} + 2\\{x_A} + 2 = - \left( {{x_B} + 2} \right)\end{array} \right.(3)$
Do $\left\{ \begin{array}{l}A \ne B\\A,{\rm{ }}B \in \left( H \right)\end{array} \right. \Rightarrow {x_A} \ne {x_B}$ nên (3) $ \Leftrightarrow {x_A} + {x_B} = - 4.$
Kết hợp với (2) ta được $\dfrac{{m - 6}}{2} = - 4 \Leftrightarrow m = - 2$ thỏa mãn (*).
Hướng dẫn giải:
- Xét phương trình hoành độ giao điểm của hai đồ thị hàm số và tìm điều kiện để phương trình có hai nghiệm phân biệt \({x_1},{x_2}\)
- Tính \(y'\) suy ra hệ số góc \({k_1},{k_2}\)
- Đánh giá GTNN của \(P\) dựa vào bất đẳng thức Cô – si cho hai số dương \(a + b \ge 2\sqrt {ab} \) dẫn đến xuất hiện tích \({k_1}.{k_2}\)
- Tìm \({k_1}.{k_2}\) bằng cách áp dụng định lý Vi – ét rồi tìm \(m\)
Giải thích thêm:
Đối với bai toán này ta có thể dùng phương pháp chọn điểm rơi, đoán rằng vai tròn của $k_1,k_2$ như nhau và dựa vào yêu cầu $P$ đạt $\min$ để đoán $k_1=k_2$, từ đó suy ra đường thẳng $y=-2x+m$ phải đi qua tâm đối xứng $I(-2;2)$ của đồ thị hàm số.
Đây không phải một cách làm chính thống nhưng có thể giúp các em nhanh đi đến đáp án trong bài thi trắc nghiệm.
Câu hỏi khác
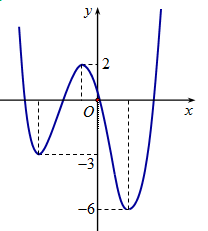
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ. Xét hàm số \(g\left( x \right) = f\left( x \right) - \dfrac{1}{3}{x^3} - \dfrac{3}{4}{x^2} + \dfrac{3}{2}x + 2018\). Mệnh đề nào dưới đây đúng?