Cho hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\). Số các giá trị tham số \(m\) để đường thẳng \(y = x + m\) luôn cắt đồ thị hàm số tại hai điểm phân biệt \(A\), \(B\) sao cho trọng tâm tam giác \(OAB\) nằm trên đường tròn \({x^2} + {y^2} - 3y = 4\) là

Cho hàm số \(f\left( x \right)\) có bảng xét dấu của đạo hàm như sau

Hàm số \(y = 3f\left( {x + 2} \right) - {x^3} + 3x\) đồng biến trên khoảng nào dưới đây ?

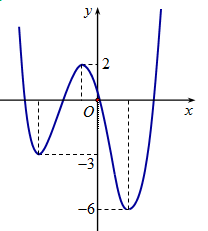
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ. Xét hàm số \(g\left( x \right) = f\left( x \right) - \dfrac{1}{3}{x^3} - \dfrac{3}{4}{x^2} + \dfrac{3}{2}x + 2018\). Mệnh đề nào dưới đây đúng?

Có bao nhiêu giá trị nguyên của tham số \(m\) để đường thẳng \(y = m\left( {x - 4} \right)\) cắt đồ thị của hàm số \(y = \left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right)\) tại bốn điểm phân biệt?

Hàm số $y = {\left( {x + m} \right)^3} + {\left( {x + n} \right)^3} - {x^3}$ (tham số $m;n$) đồng biến trên khoảng $\left( { - \infty ;\, + \infty } \right)$. Giá trị nhỏ nhất của biểu thức $P = 4\left( {{m^2} + {n^2}} \right) - m - n$ bằng

Hình vẽ bên là đồ thị của hàm số $y = f\left( x \right)$.

Gọi $S$ là tập hợp các giá trị nguyên dương của tham số $m$ để hàm số $y = \left| {f\left( {x - 1} \right) + m} \right|$ có $5$ điểm cực trị. Tổng giá trị tất cả các phần tử của $S$ bằng

Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y = {\sin ^3}x - 3{\cos ^2}x - m\sin x - 1\) đồng biến trên đoạn \(\left[ {0;\dfrac{\pi }{2}} \right]\)

Cho hàm số $y = \dfrac{{{x^3}}}{3} - a{x^2} - 3ax + 4$. Để hàm số đạt cực trị tại ${x_1}$, ${x_2}$ thỏa mãn $\dfrac{{x_1^2 + 2a{x_2} + 9a}}{{{a^2}}} + \dfrac{{{a^2}}}{{x_2^2 + 2a{x_1} + 9a}} = 2$ thì $a$ thuộc khoảng nào ?