Trong không gian Oxyz, cho 2 điểm $A\left( {1;2; - 3} \right),\,M\left( { - 2; - 2;1} \right)$ và đường thẳng $d:\dfrac{{x + 1}}{2} = \dfrac{{y - 5}}{2} = \dfrac{z}{{ - 1}}$. $\Delta $ là đường thẳng đi qua M và vuông góc với đường thẳng d đồng thời cách A một khoảng lớn nhất, khi đó $\Delta $ đi qua điểm nào trong các điểm sau:
$\Delta $ là đường thẳng đi qua M và cách A một khoảng lớn nhất khi $AM \bot \Delta $, khi đó $\Delta $ có 1 VTPT là $\overrightarrow {AM} \left( { - 3; - 4;4} \right)$
Đường thẳng d có 1 VTCP $\overrightarrow {{u_d}} \left( {2;2; - 1} \right)$. Vì $\Delta $ vuông góc với đường thẳng d nên $\Delta $ nhận $\overrightarrow {{u_d}} \left( {2;2; - 1} \right)$ là 1 VTPT.
Ta có: $\left[ {\overrightarrow {AM} ;\overrightarrow {{u_d}} } \right] = \left( { - 4;5;2} \right)$
Khi đó, $\Delta $ có 1 VTCP $\overrightarrow u \left( { - 4;5;2} \right)$. Phương trình đường thẳng $\Delta $ là: $\left\{ \begin{array}{l}x = - 2 - 4t\\y = - 2 + 5t\\z = 1 + 2t\end{array} \right.$
* Kiểm tra các điểm có thuộc $\Delta $ hay không:
+) $\left( { - 1; - 2;3} \right)$:
Ta có: $\left\{ \begin{array}{l} - 1 = - 2 - 4t\\ - 2 = - 2 + 5t\\3 = 1 + 2t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = - \dfrac{1}{4}\\t = 0\\t = 1\end{array} \right.$ (vô lý) $ \Rightarrow \left( { - 1; - 2;3} \right) \notin \Delta $
+) $\left( {2; - 7; - 1} \right)$
Ta có: $\left\{ \begin{array}{l}2 = - 2 - 4t\\ - 7 = - 2 + 5t\\ - 1 = 1 + 2t\end{array} \right. \Leftrightarrow t = - 1$ $ \Rightarrow \left( {2; - 7; - 1} \right) \in \Delta $
+)$\left( { - 1;2;3} \right)$
Ta có: $\left\{ \begin{array}{l} - 1 = - 2 - 4t\\2 = - 2 + 5t\\3 = 1 + 2t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = - \dfrac{1}{4}\\t = \dfrac{4}{5}\\t = 1\end{array} \right.$ (vô lý) $ \Rightarrow \left( { - 1;2;3} \right) \notin \Delta $
+)$\left( { - 1; - 1; - 3} \right)$
Ta có: $\left\{ \begin{array}{l} - 1 = - 2 - 4t\\ - 1 = - 2 + 5t\\ - 3 = 1 + 2t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = - \dfrac{1}{4}\\t = \dfrac{1}{5}\\t = - 2\end{array} \right.$ (vô lý) $ \Rightarrow \left( { - 1; - 1; - 3} \right) \notin \Delta $
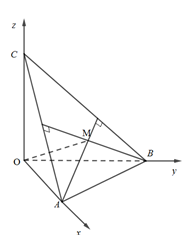
Trong không gian Oxyz, cho $M\left( { - 1;3;4} \right)$, mặt phẳng (P) đi qua M cắt các trục Ox, Oy, Oz tại các điểm A, B, C sao cho M là trực tâm $\Delta ABC$. Thể tích khối tứ diện OABC bằng
+) Ta có:
$AM \bot CB$(vì M là trực tâm tam giác ABC)
$OA \bot CB$ (vì $OA \bot OB,\,\,OA \bot OC \Rightarrow OA \bot \left( {OBC} \right) \Leftrightarrow OA \bot BC$)
$ \Rightarrow BC \bot \left( {OMA} \right) \Rightarrow BC \bot OM$
Tương tự, chứng minh được $AC \bot OM \Rightarrow OM \bot \left( {ABC} \right)$
+) Viết phương trình mặt phẳng $\left( {ABC} \right)$:
$M\left( { - 1;3;4} \right),\,\,\overrightarrow {OM} \left( { - 1;3;4} \right)$
Phương trình mặt phẳng (ABC): $ - 1\left( {x + 1} \right) + 3\left( {y - 3} \right) + 4\left( {z - 4} \right) = 0 \Leftrightarrow - x + 3y + 4z - 26 = 0$
+) Tìm tọa độ các điểm A, B, C:
Cho $y = z = 0 \Rightarrow x = 26 \Rightarrow A\left( {26;0;0} \right)$
Cho $x = z = 0 \Rightarrow y = \dfrac{{26}}{3} \Rightarrow B\left( {0;\dfrac{{26}}{3};0} \right)$
Cho $x = y = 0 \Rightarrow z = \dfrac{{13}}{2} \Rightarrow C\left( {0;0;\dfrac{{13}}{2}} \right)$
Thể tích khối tứ diện OABC : $V = \dfrac{1}{6}.26.\dfrac{{26}}{3}.\dfrac{{13}}{2} = \dfrac{{2197}}{9}$.
Trong không gian Oxyz, cho 3 điểm $A\left( {0;1;1} \right),\,B\left( {3;0; - 1} \right),\,C\left( {0;21; - 19} \right)$ và mặt cầu $\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 1$. Điểm M thuộc mặt cầu (S) sao cho tổng $3M{A^2} + 2M{B^2} + M{C^2}$ đạt giá trị nhỏ nhất, khi đó, độ dài vectơ $\overrightarrow {OM} $ là
+) Mặt cầu $\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 1$ có tâm $J\left( {1;1;1} \right)$, bán kính $R = 1$.
+) Tìm $I$: $3\overrightarrow {IA} + 2\overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \Leftrightarrow 6\overrightarrow {IA} + 2\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {IA} = - \dfrac{{2\overrightarrow {AB} + \overrightarrow {AC} }}{6}$
Ta có: $A\left( {0;1;1} \right),\,B\left( {3;0; - 1} \right),\,C\left( {0;21; - 19} \right) \Rightarrow \overrightarrow {IA} \left( { - {x_I};1 - {y_I};1 - {z_I}} \right),\,\,\overrightarrow {AB} \left( {3; - 1; - 2} \right),\,\,\overrightarrow {AC} \left( {0;20; - 20} \right)$
$ \Rightarrow \left\{ \begin{array}{l} - {x_I} = - \dfrac{{2.3 + 0}}{6}\\1 - {y_I} = - \dfrac{{2.\left( { - 1} \right) + 20}}{6}\\1 - {z_I} = - \dfrac{{2.\left( { - 2} \right) + \left( { - 20} \right)}}{6}\end{array} \right. \Rightarrow I\left( {1;4; - 3} \right)$
+) Ta có:
$\begin{array}{l}3M{A^2} + 2M{B^2} + M{C^2} = 3{\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} + 2{\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)^2}\\ = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2} + 2.\overrightarrow {MI} .\left( {3\overrightarrow {IA} + 2\overrightarrow {IB} + \overrightarrow {IC} } \right) = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2} + 2.\overrightarrow {MI} .\overrightarrow 0 \\ = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2}\end{array}$
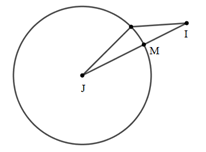
Để tổng trên là nhỏ nhất thì MI nhỏ nhất $ \Rightarrow M$là giao điểm của đoạn thẳng $IJ$ và mặt cầu $\left( S \right)$.
$\overrightarrow {JI} = \left( {0;3; - 4} \right)$
$ \Rightarrow $Tọa độ điểm $M$thuộc đoạn IJ có dạng $\left( {1;1 + 3t;1 - 4t} \right),\,\,t \in \left[ {0;1} \right]$
Mặt khác $M \in \left( S \right) \Rightarrow {\left( {1 - 1} \right)^2} + {\left( {1 - \left( {1 + 3t} \right)} \right)^2} + {\left( {1 - \left( {1 - 4t} \right)} \right)^2} = 1$
$ \Leftrightarrow {t^2} = \dfrac{1}{{25}} \Leftrightarrow \left[ \begin{array}{l}t = \dfrac{1}{5}\\t = - \dfrac{1}{5}\,(L)\end{array} \right. \Leftrightarrow t = \dfrac{1}{5}$ $ \Rightarrow M\left( {1;\dfrac{8}{5};\dfrac{1}{5}} \right) \Rightarrow OM = \dfrac{{3\sqrt {10} }}{5}$.
Trong không gian Oxyz, cho mặt cầu $(S):{x^2} + {y^2} + {z^2} - 6x + 4y - 2z + 5 = 0$. Phương trình mặt phẳng $(Q)$chứa trục Ox và cắt $(S)$ theo giao tuyến là một đường tròn bán kính bằng 2 là
$(S):{x^2} + {y^2} + {z^2} - 6x + 4y - 2z + 5 = 0 \Leftrightarrow {(x - 3)^2} + {(y + 2)^2} + {(z - 1)^2} = 9$
$ \Rightarrow \left( S \right)$ có tâm $I(3; - 2;1)$, bán kính $R = 3$.
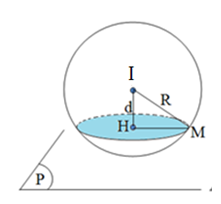
$(Q)$ cắt $(S)$ theo giao tuyến là một đường tròn bán kính $r = 2$
Ta có: ${d^2} + {r^2} = {R^2} \Leftrightarrow {d^2} + {2^2} = {3^2} \Leftrightarrow d = \sqrt 5 $
Gọi $\overrightarrow n (a;b;c),\,\,\,\left( {\overrightarrow n \ne \overrightarrow 0 } \right)$ là một VTPT của (Q). Khi đó $\overrightarrow n $ vuông góc với VTCP $\overrightarrow u (1;0;0)$của Ox $ \Rightarrow 1.a + 0.b + 0.c = 0 \Leftrightarrow a = 0$
Phương trình mặt phẳng (Q) đi qua O(0;0;0) và có VTPT $\overrightarrow n (0;b;c),\,\,\,\left( {\overrightarrow n \ne \overrightarrow 0 } \right)$ là:
$0.(x - 0) + b(y - 0) + c(z - 0) = 0 \Leftrightarrow by + cz = 0$
Khoảng cách từ tâm I đến (Q):
$d = \dfrac{{\left| {b.( - 2) + c.1} \right|}}{{\sqrt {{b^2} + {c^2}} }} = \sqrt 5 \Rightarrow {\left( {2b - c} \right)^2} = 5({b^2} + {c^2}) \Leftrightarrow {b^2} + 4bc + 4{c^2} = 0 \Leftrightarrow {(b + 2c)^2} = 0 \Leftrightarrow b = - 2c$
Cho $c = - 1 \Rightarrow b = 2 \Rightarrow \overrightarrow n (0;2; - 1)$. Phương trình mặt phẳng (Q): $2y - z = 0$.
Cho ba tia Ox, Oy, Oz đôi một vuông góc với nhau. Gọi C là điểm cố định trên Oz, đặt OC = 1, các điểm A, B thay đổi trên Ox, Oy sao cho $OA + OB = OC$. Giá trị bé nhất của bán kính mặt cầu ngoại tiếp tứ diện OABC là
Đặt $A\left( {x;0;0} \right),\,\,B\left( {0;y;0} \right),\,\,\left( {x,y > 0} \right)$
Vì $OA + OB = OC = 1 \Rightarrow x + y = 1$
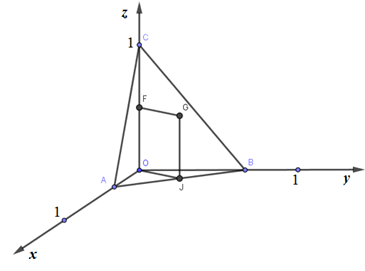
Gọi J, F lần lượt là trung điểm AB, OC. Kẻ đường thẳng qua F song song OJ, đường thẳng qua J song song OC, 2 đường thẳng này cắt nhau tại G.
$\Delta OAB$ vuông tại O $ \Rightarrow J$ là tâm đường tròn ngoại tiếp tam giác.
$GJ//OC \Rightarrow GJ \bot (OAB) \Rightarrow GO = GA = GB$
$GF//JO,\,\,JO \bot OC \Rightarrow GF \bot OC$, mà F là trung điểm của OC
$ \Rightarrow GF$ là đường trung trực của OC $ \Rightarrow GC = GO$
$ \Rightarrow GO = GA = GB = GC \Rightarrow G$ là tâm mặt cầu ngoại tiếp tứ diện OABC
Bán kính mặt cầu ngoại tiếp tứ diện OABC : $R = OG = FJ = \sqrt {O{F^2} + O{J^2}} = \sqrt {{{\left( {\dfrac{1}{2}} \right)}^2} + O{J^2}} $
Ta có: $OJ = \dfrac{{AB}}{2} = \dfrac{{\sqrt {{x^2} + {y^2}} }}{2} \ge \dfrac{{\sqrt {\dfrac{{{{(x + y)}^2}}}{2}} }}{2} = \dfrac{{\sqrt {\dfrac{{{1^2}}}{2}} }}{2} = \dfrac{{\sqrt 2 }}{4}$$ \Rightarrow R \ge \sqrt {{{\left( {\dfrac{1}{2}} \right)}^2} + {{\left( {\dfrac{{\sqrt 2 }}{4}} \right)}^2}} = \sqrt {\dfrac{3}{8}} \Rightarrow {R_{\min }} = \sqrt {\dfrac{3}{8}} = \dfrac{{\sqrt 6 }}{4}$
Trong không gian Oxyz cho $A( - 4;7;5)$ và hai đường thẳng ${d_1}:\left\{ \begin{array}{l}x = 1 - t\\y = 3t\\z = - 2 + t\end{array} \right.$; ${d_2}:\dfrac{{x + 1}}{3} = \dfrac{{y - 2}}{4} = z - 1$. Đường thẳng d đi qua A đồng thời cắt ${d_1},\,\,{d_2}$có phương trình là:
Gọi M, N lần lượt là giao điểm của d và ${d_1},\,\,{d_2}$ $ \Rightarrow $Giả sử $M(1 - t;3t; - 2 + t),\,\,N( - 1 + 3{t_1};2 + 4{t_1};\,\,1 + {t_1})$
$ \Rightarrow \overrightarrow {MA} = \left( { - 5 + t;7 - 3t;7 - t} \right),\,\,\overrightarrow {MB} = \left( { - 3 - 3{t_1};5 - 4{t_1};4 - {t_1}} \right)$
Vì A, M, N thẳng hàng nên $\dfrac{{ - 5 + t}}{{ - 3 - 3{t_1}}} = \dfrac{{7 - 3t}}{{5 - 4{t_1}}} = \dfrac{{7 - t}}{{4 - {t_1}}} \Leftrightarrow \left\{ \begin{array}{l}\left( { - 5 + t} \right)\left( {5 - 4{t_1}} \right) = \left( {7 - 3t} \right)\left( { - 3 - 3{t_1}} \right)\\\left( { - 5 + t} \right)\left( {4 - {t_1}} \right) = \left( {7 - t} \right)\left( { - 3 - 3{t_1}} \right)\end{array} \right.$
$\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} - 25 + 20{t_1} + 5t - 4t{t_1} = - 21 - 21{t_1} + 9t + 9t{t_1}\\ - 20 + 5{t_1} + 4t - t{t_1} = - 21 - 21{t_1} + 3t + 3t{t_1}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}41{t_1} - 4t - 13t{t_1} = 4\\26{t_1} + t - 4t{t_1} = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}41{t_1} - 4t - 13t{t_1} = 4\\104{t_1} + 4t - 16t{t_1} = - 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}145{t_1} - 29t{t_1} = 0\\26{t_1} + t - 4t{t_1} = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}{t_1} = 0\\t = 5\end{array} \right.\\26{t_1} + t - 4t{t_1} = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{t_1} = 0\\t = - 1\end{array} \right.\\\left\{ \begin{array}{l}t = 5\\{t_1} = - 1\end{array} \right.\,\,(L)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{t_1} = 0\\t = - 1\end{array} \right.\end{array}$
$ \Rightarrow \overrightarrow {MA} = \left( { - 6;10;8} \right),\,\,M\left( {2; - 3; - 3} \right)$
Phương trình đường thẳng d đi qua $M\left( {2; - 3; - 3} \right)$ và có 1 VTCP $\overrightarrow u = \left( { - 3;5;4} \right)$ là: $\left\{ \begin{array}{l}x = 2 - 3t\\y = - 3 + 5t\\z = - 3 + 4t\end{array} \right.$
Trong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \(A\left( {1;0;3} \right),B\left( {11; - 5; - 12} \right)\). Điểm \(M\left( {a;b;c} \right)\) thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho \(3M{A^2} + 2M{B^2}\) nhỏ nhất. Tính \(P = a + b + c\)
\(M\left( {a;b;c} \right) \in \left( {Oxy} \right) \Rightarrow c = 0 \Rightarrow M\left( {a;b;0} \right)\)
\(\begin{array}{l} \Rightarrow 3M{A^2} + 2M{B^2} = 3\left[ {{{\left( {a - 1} \right)}^2} + {b^2} + 9} \right] + 2\left[ {{{\left( {a - 11} \right)}^2} + {{\left( {b + 5} \right)}^2} + {{12}^2}} \right]\\ = 3\left( {{a^2} - 2a + {b^2} + 10} \right) + 2\left( {{a^2} - 22a + {b^2} + 10b + 290} \right)\\ = 3{a^2} - 6a + 3{b^2} + 30 + 2{a^2} - 44a + 2{b^2} + 20b + 580\\ = 5{a^2} - 50a + 5{b^2} + 20b + 610\\ = 5\left( {{a^2} - 10a + {b^2} + 4b + 122} \right)\\ = 5\left[ {{{\left( {a - 5} \right)}^2} + {{\left( {b + 2} \right)}^2} + 93} \right] \ge 465\end{array}\)
Dấu bằng xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a = 5\\b = - 2\end{array} \right. \Rightarrow P = a + b + c = 5 - 2 + 0 = 3\)
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \({d_1}:\dfrac{{x - 2}}{{ - 1}} = \dfrac{y}{1} = \dfrac{z}{1}\) và \({d_2}:\dfrac{x}{{ - 2}} = \dfrac{{y - 1}}{1} = \dfrac{{z - 2}}{1}.\) Phương trình mặt phẳng (P) song song và cách đều hai đường thẳng \({d_1},{d_2}\) là:
Ta có \({d_1}:\dfrac{{x - 2}}{{ - 1}} = \dfrac{y}{1} = \dfrac{z}{1} \Rightarrow vtcp\,\,\overrightarrow {{u_1}} = \left( { - 1;1;1} \right)\)
\({d_2}:\dfrac{x}{{ - 2}} = \dfrac{{y - 1}}{1} = \dfrac{{z - 2}}{1}. \Rightarrow vtcp\,\,\overrightarrow {{u_2}} \left( { - 2;1;1} \right)\)
Khi đó ta có \(vtpt\,\overrightarrow {\,n} = \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = \left( {0; - 1;1} \right)\)
Khi đó phương trình mặt phẳng (P) có dạng: \( - y + z + D = 0\)
Ta lại có: Phương trình mặt phẳng (P) cách đều hai đường thẳng \({d_1},{d_2}\)nên: \(d\left( {{d_1};\left( P \right)} \right) = d\left( {{d_2};\left( P \right)} \right) \Leftrightarrow d\left( {A;\left( P \right)} \right) = d\left( {B;\left( P \right)} \right)\) với \(A\left( {2;0;0} \right);B\left( {0;1;2} \right)\)
\( \Leftrightarrow \dfrac{{\left| D \right|}}{{\sqrt {1 + 1} }} = \dfrac{{\left| { - 1 + 2 + D} \right|}}{{\sqrt {1 + 1} }} \Leftrightarrow \left| D \right| = \left| {D + 1} \right| \Leftrightarrow \left[ \begin{array}{l}D = D + 1\\D = - D - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}0 = 1\left( {vn} \right)\\D = \dfrac{{ - 1}}{2}\end{array} \right.\)
Vậy phương trình mặt phẳng (P) cần tìm là: \( - y + z - \dfrac{1}{2} = 0 \Leftrightarrow 2y - 2z + 1 = 0\)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} + {z^2} - 4x + 10y - 2z - 6 = 0\). Cho m là số thực thỏa mãn giao tuyến của hai mặt phẳng \(y = m\) và \(x + z - 3 = 0\) tiếp xúc với mặt cầu \(\left( S \right)\). Tích tất cả các giá trị mà m có thể nhận được bằng:
Bước 1:
Mặt cầu \(\left( S \right)\) có tâm \(I\left( {2; - 5;1} \right)\), bán kính \(R = \sqrt {4 + 25 + 1 + 6} = 6\).
Giao tuyến của hai mặt phẳng \(y = m\) và \(x + z - 3 = 0\) là nghiệm của hệ phương trình $\;\left\{ \begin{array}{l}y = m\\x + z - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = t\\y = m\\z = 3 - t\end{array} \right.\,\,\left( d \right) $
$\Rightarrow $Đường thẳng (d) đi qua \(M\left( {0;m;3} \right)\) và có 1 VTCP là \(\overrightarrow u = \left( {1;0; - 1} \right)\).
Bước 2:
Đường thẳng (d) tiếp xúc với mặt cầu \(\left( S \right) \Leftrightarrow d\left( {I;d} \right) = R\).
\( \Rightarrow \dfrac{{\left| {\left[ {\overrightarrow {IM} ;\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}} = R \Leftrightarrow \dfrac{{\left| {m + 5} \right|\sqrt 2 }}{{\sqrt 2 }} = 6 \Leftrightarrow \left[ \begin{array}{l}m + 5 = 6\\m + 5 = - 6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 11\end{array} \right.\)
Vậy tích các giá trị của m là $1.(-11)=-11$
Trong không gian với hệ tọa độ Oxyz cho ba điểm \(A\left( {2;0;0} \right);\,\,B\left( {0;4;0} \right);\,\,C\left( {0;0;6} \right)\). Điểm M thay đổi trên mặt phẳng \(\left( {ABC} \right)\) và điểm N là điểm trên tia OM sao cho \(OM.ON = 12\). Biết rằng khi M thay đổi, điểm N luôn thuộc một mặt cầu cố định. Tìm bán kính của mặt cầu đó?
Gọi điểm \(N\left( {x;y;z} \right)\).
Ta có O, M, N thẳng hàng \( \Rightarrow OM.ON = \overrightarrow {OM} .\overrightarrow {ON} = 12\)
\(\begin{array}{l} \Rightarrow \overrightarrow {OM} = \dfrac{{12}}{{\overrightarrow {ON} }} = \dfrac{{12}}{{O{N^2}}}.\overrightarrow {ON} = \dfrac{{12}}{{{x^2} + {y^2} + {z^2}}}\left( {x;y;z} \right)\\ \Rightarrow M\left( {\dfrac{{12x}}{{{x^2} + {y^2} + {z^2}}};\dfrac{{12y}}{{{x^2} + {y^2} + {z^2}}};\dfrac{{12z}}{{{x^2} + {y^2} + {z^2}}}} \right)\end{array}\)
Mặt phẳng \(\left( {ABC} \right)\) có phương trình \(\dfrac{x}{2} + \dfrac{y}{4} + \dfrac{z}{6} = 1 \Leftrightarrow 6x + 3y + 2z - 12 = 0\)
Do \(M \in \left( {ABC} \right)\) nên thay tọa độ điểm M vào phương trình mặt phẳng (ABC) ta có:
\(\begin{array}{l}6\dfrac{{12x}}{{{x^2} + {y^2} + {z^2}}} + 3\dfrac{{12y}}{{{x^2} + {y^2} + {z^2}}} + 2\dfrac{{12z}}{{{x^2} + {y^2} + {z^2}}} - 12 = 0\\ \Leftrightarrow 6x + 3y + 2z - \left( {{x^2} + {y^2} + {z^2}} \right) = 0\\ \Leftrightarrow {x^2} + {y^2} + {z^2} - 6x - 3y - 2z = 0\end{array}\)
Vậy khi M thay đổi trên \(\left( {ABC} \right)\) thì N luôn thuộc mặt cầu tâm \(I\left( {3;\dfrac{3}{2};1} \right)\), bán kính \(R = \sqrt {9 + \dfrac{9}{4} + 1} = \dfrac{7}{2}\).
Trong không gian với hệ tọa độ Oxyz cho ba điểm \(A\left( {2; - 1;1} \right);\,\,M\left( {5;3;1} \right);\,\,N\left( {4;1;2} \right)\) và mặt phẳng \(\left( P \right):\,\,y + z = 27\) . Biết rằng tồn tại điểm B trên tia AM, điểm C trên \(\left( P \right)\) và điểm D trên tia AN sao cho tứ giác \(ABCD\) là hình thoi. Tọa độ điểm C là:
Ta có \(\overrightarrow {AM} = \left( {3;4;0} \right);\,\,\overrightarrow {AN} = \left( {2;2;1} \right)\)
\( \Rightarrow \) phương trình đường thẳng AM và AN lần lượt là :
\(\begin{array}{l}\left( {AM} \right):\,\,\left\{ \begin{array}{l}x = 2 + 3t\\y = - 1 + 4t\\z = 1\end{array} \right.;\,\,\,\left( {AN} \right):\,\,\left\{ \begin{array}{l}x = 2 + 2t'\\y = - 1 + 2t'\\z = 1 + t'\end{array} \right.\\B \in AM \Rightarrow B\left( {2 + 3t; - 1 + 4t;1} \right);\,\,\,D \in AN \Rightarrow D\left( {2 + 2t'; - 1 + 2t';1 + t'} \right)\\ \Rightarrow \overrightarrow {AB} = \left( {3t;4t;0} \right);\,\,\overrightarrow {DC} = \left( {{x_C} - 2 - 2t';\,{y_C} + 1 - 2t';{z_C} - 1 - t'} \right)\end{array}\)
Do \(ABCD\) là hình thoi \( \Rightarrow \overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ \begin{array}{l}{x_C} - 2 - 2t' = 3t\\{y_C} + 1 - 2t' = 4t\\{z_C} - 1 - t' = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3t + 2t' + 2\\{y_C} = 4t + 2t' - 1\\{z_C} = t' + 1\end{array} \right.\)
Mà \(C \in \left( P \right) \Rightarrow 4t + 2t' - 1 + t' + 1 = 27 \Leftrightarrow 4t + 3t' = 27\)
ABCD là hình thoi \( \Rightarrow \overrightarrow {AC} \bot \overrightarrow {BD} \Rightarrow \overrightarrow {AC} .\overrightarrow {BD} = 0\)
Ta có \(\overrightarrow {AC} = \left( {3t + 2t';4t + 2t';t'} \right);\,\,\overrightarrow {BD} = \left( {2t' - 3t;2t' - 4t;t'} \right)\)
\(\begin{array}{l} \Rightarrow \left( {3t + 2t'} \right)\left( {2t' - 3t} \right) + \left( {4t + 2t'} \right)\left( {2t' - 4t} \right) + t{'^2} = 0\\ \Leftrightarrow 4t{'^2} - 9{t^2} + 4t{'^2} - 16{t^2} + t{'^2} = 0\\ \Leftrightarrow 9t{'^2} = 25{t^2}\\ \Leftrightarrow 3t' = \pm 5t\end{array}\)
TH1 : \(\left\{ \begin{array}{l}4t + 3t' = 27\\3t' = 5t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = 3\\t' = 5\end{array} \right. \Rightarrow C\left( {21;21;6} \right)\)
TH2 : \(\left\{ \begin{array}{l}4t + 3t' = 27\\3t' = - 5t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = - 27\\t' = 45\end{array} \right. \Rightarrow C\left( {11; - 19;46} \right)\)
Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng \(\left( P \right):\,\,x - 2y + 2z + 1 = 0\); \(\left( Q \right):\,\,x - 2y + 2z - 8 = 0;\,\,\left( R \right):\,\,x - 2y + 2z + 4 = 0.\) Một đường thẳng \(\Delta \) thay đổi cắt ba mặt phẳng \(\left( P \right);\,\,\left( Q \right);\,\,\left( R \right)\) lần lượt tại các điểm A, B, C. Giá trị nhỏ nhất của biểu thức \(AB + \dfrac{{96}}{{A{C^2}}}\) là:
Nhận xét \(\left( P \right)//\left( Q \right)//\left( R \right)\) và (P) nằm giữa (Q) và (R).
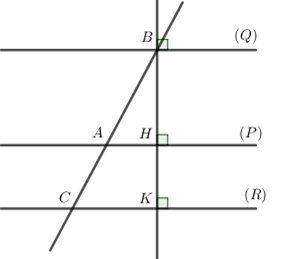
Ta có \(BH = d\left( {\left( Q \right);\left( P \right)} \right) = 9;\,\,HK = d\left( {\left( P \right);\left( R \right)} \right) = 3\)
Áp dụng định lí Ta-lét ta có: \(\dfrac{{AB}}{{AC}} = \dfrac{{BH}}{{HK}} = 3\).
Áp dụng BĐT Cauchy ta có :
\(\begin{array}{l}AB + \dfrac{{96}}{{A{C^2}}} = \dfrac{{AB}}{2} + \dfrac{{AB}}{2} + \dfrac{{96}}{{A{C^2}}}\mathop \ge \limits^{Cauchy} 3\sqrt[3]{{\dfrac{{AB}}{2}.\dfrac{{AB}}{2}.\dfrac{{96}}{{A{C^2}}}}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 3.\sqrt[3]{{24.{{\left( {\dfrac{{AB}}{{AC}}} \right)}^2}}} = 3.\sqrt[3]{{24.9}} = 18\end{array}\)
Trong không gian \(Oxyz\), cho mặt cầu \((S_1)\) có tâm \(I(2;1;1)\) có bán kính bằng \(4\) và mặt cầu \((S_2)\) có tâm \(J(2;1;5)\) có bán kính bằng \(2\). \((P)\) là mặt phẳng thay đổi tiếp xúc với hai mặt cầu \((S_1), (S_2)\). Đặt \(M, m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của khoảng cách từ điểm \(O\) đến \((P)\). Giá trị \(M + m\) bằng?
Giả sử \((P)\) tiếp xúc với \((S_1), (S_2)\) lần lượt tại \(A,B\).
Gọi $IJ \cap \left( P \right) = M$ ta kiểm tra được \(J\) là trung điểm \(IM \) do \(\dfrac{{IA}}{{JB}} = \dfrac{{MI}}{{MJ}} = 2\) suy ra \(M\left( {2;1;9} \right)\)
Gọi \(\overrightarrow n = \left( {a;b;c} \right),\,\left( {{a^2} + {b^2} + {c^2} \ne 0} \right)\) suy ra \(\left( P \right):\,a\left( {x - 2} \right) + b\left( {y - 1} \right) + c\left( {z - 9} \right) = 0\)
Ta có: \(\left\{ \begin{array}{l}d\left( {I;\left( P \right)} \right) = {R_1} = 4\\d\left( {J;\left( P \right)} \right) = {R_2} = 2\end{array} \right. \Rightarrow \dfrac{{\left| c \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }} = \dfrac{1}{2} \Leftrightarrow {a^2} + {b^2} = 3{c^2} \Leftrightarrow {\left( {\dfrac{a}{c}} \right)^2} + {\left( {\dfrac{b}{c}} \right)^2} = 3\left( 1 \right)\)
Ta có: \(d\left( {O;\left( P \right)} \right) = \dfrac{{\left| {2a + b + 9c} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }} = \dfrac{{\left| {2a + b + 9c} \right|}}{{2\left| c \right|}} = \dfrac{1}{2}\left| {\dfrac{{2a}}{c} + \dfrac{b}{c} + 9} \right|\)
Đặt \(t = \dfrac{{2a}}{c} + \dfrac{b}{c} \Leftrightarrow \dfrac{b}{c} = t - \dfrac{{2a}}{c}\) ta được \(d\left( {O;\left( P \right)} \right) = \dfrac{1}{2}\left| {t + 9} \right|\)
Thay \(\dfrac{b}{c} = t - \dfrac{{2a}}{c}\) vào (1) ta thu được \({\left( {\dfrac{a}{c}} \right)^2} + {\left( {t - \dfrac{{2a}}{c}} \right)^2} = 3 \Leftrightarrow 5{\left( {\dfrac{a}{c}} \right)^2} - 4\dfrac{a}{c}t + {t^2} - 3 = 0\)
Để phương trình có nghiệm thì \(4{t^2} - 5{t^2} + 15 \ge 0 \Leftrightarrow - \sqrt {15} \le t \le \sqrt {15} \Leftrightarrow 0 < 9 - \sqrt {15} \le t + 9 \le 9 + \sqrt {15} \)
Suy ra \(\dfrac{{9 - \sqrt {15} }}{2} \le d\left( {O;\left( P \right)} \right) \le \dfrac{{9 + \sqrt {15} }}{2} \Rightarrow M = \dfrac{{9 + \sqrt {15} }}{2};m = \dfrac{{9 - \sqrt {15} }}{2}\)
Suy ra \(M + m = 9\).
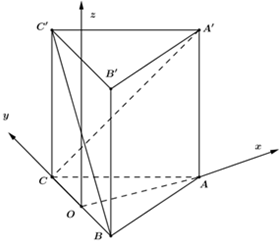
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh bên bằng cạnh đáy. Đường thằng \(MN\,\left( {M \in A'C,N \in BC'} \right)\) là đường vuông góc chung của A’C và BC’. Tỉ số \(\dfrac{{NB}}{{NC'}}\) bằng
Xét hình lăng trụ tam giác đều có các cạnh đều bằng \(2\).
Chọn hệ trục tọa độ như hình vẽ có gốc tọa độ là trung điểm của \(BC.\)
Ta có các điểm: \(O\left( {0;\;0;\;0} \right);\;A \in Ox \Rightarrow A\left( {\sqrt 3 ;\;0;\;0} \right)\)
\(\begin{array}{l}B;\;C \in Oy \Rightarrow B\left( {0;\; - 1;\;0} \right),\;\;C\left( {0;\;1;\;0} \right).\\A'\left( {\sqrt 3 ;\;0;\;2} \right);\;C'\left( {0;\;1;\;2} \right).\\ \Rightarrow \overrightarrow {A'C} = \left( { - \sqrt 3 ;\;1;\; - 2} \right);\;\;\overrightarrow {BC} = \left( {0;\;2;\;2} \right) = \left( {0;\;1;\;1} \right).\end{array}\)
Phương trình đường thẳng \(A'C\) là: \(\left\{ \begin{array}{l}x = - \sqrt 3 {t_1}\\y = 1 + {t_1}\\z = - 2{t_1}\end{array} \right..\)
Phương trình đường thẳng \(BC'\) là: \(\left\{ \begin{array}{l}x = 0\\y = - 1 + {t_2}\\z = {t_2}\end{array} \right..\)
Ta có điểm \(M \in A'C \Rightarrow M\left( { - \sqrt 3 {t_1};1 + {t_1}; - 2{t_1}} \right);\;N \in BC' \Rightarrow N\left( {0;\; - 1 + {t_2};\;{t_2}} \right).\)
\( \Rightarrow \overrightarrow {MN} \left( {\sqrt 3 {t_1};\;{t_2} - {t_1} - 2;\;{t_2} + 2{t_1}} \right)\)
\(MN\) là đoạn vuông góc chung của \(A'C\) và \(BC' \Rightarrow \left\{ \begin{array}{l}MN \bot A'C\\MN \bot BC'\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow {MN} .\overrightarrow {AC'} = 0\\\overrightarrow {MN} .\overrightarrow {BC'} = 0\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} - \sqrt 3 {t_1}.\sqrt 3 + {t_2} - {t_1} - 2 - 2\left( {{t_2} + 2{t_1}} \right) = 0\\{t_2} - {t_1} - 2 + {t_2} + 2{t_1} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 8{t_1} - {t_2} = 2\\{t_1} + 2{t_2} = 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{t_1} = - \dfrac{2}{5}\\{t_2} = \dfrac{6}{5}\end{array} \right. \Rightarrow N\left( {0;\;\dfrac{1}{5};\;\dfrac{6}{5}} \right) \Rightarrow \left\{ \begin{array}{l}\overrightarrow {NB} = \left( {0;\; - \dfrac{6}{5};\; - \dfrac{6}{5}} \right)\\\overrightarrow {NC'} = \left( {0;\;\dfrac{4}{5};\;\dfrac{4}{5}\;} \right)\end{array} \right..\\ \Rightarrow \dfrac{{NB}}{{NC}} = \dfrac{{\left| {\overrightarrow {NB} } \right|}}{{\left| {\overrightarrow {NC'} } \right|}} = \dfrac{{\sqrt {\dfrac{{36}}{{25}}.2} }}{{\sqrt {\dfrac{{16}}{{25}}.2} }} = \sqrt {\dfrac{9}{4}} = \dfrac{3}{2}.\end{array}\)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: $\dfrac{{x - 13}}{{ - 1}} = \dfrac{{y + 1}}{1} = \dfrac{z}{4}$ và mặt cầu $(S):{x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 67 = 0$. Qua d dựng các mặt phẳng tiếp xúc với (S) lần lượt tại ${T_1},\,\,{T_2}$. Tìm tọa độ trung điểm H của ${T_1}{T_2}$.
$(S):{x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 67 = 0$ có tâm $I\left( {1;2;3} \right)$, bán kính $R = 9$.
Gọi $M$ là hình chiếu vuông góc của $I$ lên đường thẳng $d$.
+) Tìm tọa độ điểm M:
Mặt phẳng $\left( \alpha \right)$qua I vuông góc d có phương trình:
$\begin{array}{l} - 1\left( {x - 1} \right) + 1\left( {y - 2} \right) + 4\left( {z - 3} \right) = 0 \Leftrightarrow - x + y + 4z - 13 = 0\\M \in d \Rightarrow M\left( {13 - t; - 1 + t;4t} \right)\\M \in \left( \alpha \right) \Rightarrow - \left( {13 - t} \right) + \left( { - 1 + t} \right) + 4.4t - 13 = 0 \Leftrightarrow 18t - 27 = 0 \Leftrightarrow t = \dfrac{3}{2}\\ \Rightarrow M\left( {\dfrac{{23}}{2};\dfrac{1}{2};6} \right) \Rightarrow IM = \dfrac{{9\sqrt 6 }}{2}\end{array}$
* Xét mặt phẳng qua I và vuông góc $d$:
H là trung điểm của ${T_1}{T_2} \Rightarrow $$H = {T_1}{T_2} \cap IM$
Khi đó, $IH = \dfrac{{{R^2}}}{{IM}} = \dfrac{{81}}{{\dfrac{{9\sqrt 6 }}{2}}} = 3\sqrt 6 \Rightarrow \dfrac{{IH}}{{IM}} = \dfrac{{3\sqrt 6 }}{{\dfrac{{9\sqrt 6 }}{2}}} = \dfrac{2}{3} \Rightarrow \overrightarrow {IH} = \dfrac{2}{3}\overrightarrow {IM} $
Ta có: $\overrightarrow {IH} = \left( {{x_H} - 1;{y_H} - 2;{z_H} - 3} \right);\,\,\,\,\overrightarrow {IM} = \left( {\dfrac{{21}}{2}; - \dfrac{3}{2};3} \right) \Rightarrow \left\{ \begin{array}{l}{x_H} = 8\\{y_H} = 1\\{z_H} = 5\end{array} \right. \Rightarrow H\left( {8;1;5} \right)$
