Câu hỏi:
2 năm trước
Trong không gian Oxyz, cho $M\left( { - 1;3;4} \right)$, mặt phẳng (P) đi qua M cắt các trục Ox, Oy, Oz tại các điểm A, B, C sao cho M là trực tâm $\Delta ABC$. Thể tích khối tứ diện OABC bằng
Trả lời bởi giáo viên
Đáp án đúng: c
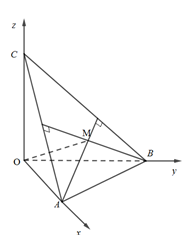
+) Ta có:
$AM \bot CB$(vì M là trực tâm tam giác ABC)
$OA \bot CB$ (vì $OA \bot OB,\,\,OA \bot OC \Rightarrow OA \bot \left( {OBC} \right) \Leftrightarrow OA \bot BC$)
$ \Rightarrow BC \bot \left( {OMA} \right) \Rightarrow BC \bot OM$
Tương tự, chứng minh được $AC \bot OM \Rightarrow OM \bot \left( {ABC} \right)$
+) Viết phương trình mặt phẳng $\left( {ABC} \right)$:
$M\left( { - 1;3;4} \right),\,\,\overrightarrow {OM} \left( { - 1;3;4} \right)$
Phương trình mặt phẳng (ABC): $ - 1\left( {x + 1} \right) + 3\left( {y - 3} \right) + 4\left( {z - 4} \right) = 0 \Leftrightarrow - x + 3y + 4z - 26 = 0$
+) Tìm tọa độ các điểm A, B, C:
Cho $y = z = 0 \Rightarrow x = 26 \Rightarrow A\left( {26;0;0} \right)$
Cho $x = z = 0 \Rightarrow y = \dfrac{{26}}{3} \Rightarrow B\left( {0;\dfrac{{26}}{3};0} \right)$
Cho $x = y = 0 \Rightarrow z = \dfrac{{13}}{2} \Rightarrow C\left( {0;0;\dfrac{{13}}{2}} \right)$
Thể tích khối tứ diện OABC : $V = \dfrac{1}{6}.26.\dfrac{{26}}{3}.\dfrac{{13}}{2} = \dfrac{{2197}}{9}$.
Hướng dẫn giải:
- Chứng minh : $OM \bot \left( {ABC} \right)$
- Viết phương trình mặt phẳng $\left( {ABC} \right)$, là mặt phẳng đi qua M và nhận $\overrightarrow {OM} $ là 1 VTPT.
- Tìm tọa độ giao điểm của (ABC) và các trục tọa độ, từ đó tính thể tích khối tứ diện OABC.
