Câu hỏi:
2 năm trước
Trong không gian Oxyz, cho mặt cầu $(S):{x^2} + {y^2} + {z^2} - 6x + 4y - 2z + 5 = 0$. Phương trình mặt phẳng $(Q)$chứa trục Ox và cắt $(S)$ theo giao tuyến là một đường tròn bán kính bằng 2 là
Trả lời bởi giáo viên
Đáp án đúng: d
$(S):{x^2} + {y^2} + {z^2} - 6x + 4y - 2z + 5 = 0 \Leftrightarrow {(x - 3)^2} + {(y + 2)^2} + {(z - 1)^2} = 9$
$ \Rightarrow \left( S \right)$ có tâm $I(3; - 2;1)$, bán kính $R = 3$.
$(Q)$ cắt $(S)$ theo giao tuyến là một đường tròn bán kính $r = 2$
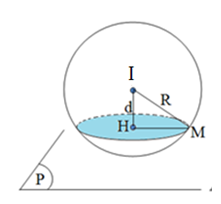
Ta có: ${d^2} + {r^2} = {R^2} \Leftrightarrow {d^2} + {2^2} = {3^2} \Leftrightarrow d = \sqrt 5 $
Gọi $\overrightarrow n (a;b;c),\,\,\,\left( {\overrightarrow n \ne \overrightarrow 0 } \right)$ là một VTPT của (Q). Khi đó $\overrightarrow n $ vuông góc với VTCP $\overrightarrow u (1;0;0)$của Ox $ \Rightarrow 1.a + 0.b + 0.c = 0 \Leftrightarrow a = 0$
Phương trình mặt phẳng (Q) đi qua O(0;0;0) và có VTPT $\overrightarrow n (0;b;c),\,\,\,\left( {\overrightarrow n \ne \overrightarrow 0 } \right)$ là:
$0.(x - 0) + b(y - 0) + c(z - 0) = 0 \Leftrightarrow by + cz = 0$
Khoảng cách từ tâm I đến (Q):
$d = \dfrac{{\left| {b.( - 2) + c.1} \right|}}{{\sqrt {{b^2} + {c^2}} }} = \sqrt 5 \Rightarrow {\left( {2b - c} \right)^2} = 5({b^2} + {c^2}) \Leftrightarrow {b^2} + 4bc + 4{c^2} = 0 \Leftrightarrow {(b + 2c)^2} = 0 \Leftrightarrow b = - 2c$
Cho $c = - 1 \Rightarrow b = 2 \Rightarrow \overrightarrow n (0;2; - 1)$. Phương trình mặt phẳng (Q): $2y - z = 0$.
Hướng dẫn giải:
${d^2} + {r^2} = {R^2}$
Trong đó,
$d$: khoảng cách từ tâm O đến mặt phẳng (P),
$r$: bán kính đường tròn là giao tuyến của mặt cầu (S) và mặt phẳng (P),
$R$: bán kính hình cầu.
