Trong không gian Oxyz, cho 3 điểm $A\left( {0;1;1} \right),\,B\left( {3;0; - 1} \right),\,C\left( {0;21; - 19} \right)$ và mặt cầu $\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 1$. Điểm M thuộc mặt cầu (S) sao cho tổng $3M{A^2} + 2M{B^2} + M{C^2}$ đạt giá trị nhỏ nhất, khi đó, độ dài vectơ $\overrightarrow {OM} $ là

+) Mặt cầu $\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 1$ có tâm $J\left( {1;1;1} \right)$, bán kính $R = 1$.

+) Tìm $I$:  $3\overrightarrow {IA}  + 2\overrightarrow {IB}  + \overrightarrow {IC}  = \overrightarrow 0  \Leftrightarrow 6\overrightarrow {IA}  + 2\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow 0  \Leftrightarrow \overrightarrow {IA}  =  - \dfrac{{2\overrightarrow {AB}  + \overrightarrow {AC} }}{6}$

Ta có: $A\left( {0;1;1} \right),\,B\left( {3;0; - 1} \right),\,C\left( {0;21; - 19} \right) \Rightarrow \overrightarrow {IA} \left( { - {x_I};1 - {y_I};1 - {z_I}} \right),\,\,\overrightarrow {AB} \left( {3; - 1; - 2} \right),\,\,\overrightarrow {AC} \left( {0;20; - 20} \right)$

$ \Rightarrow \left\{ \begin{array}{l} - {x_I} =  - \dfrac{{2.3 + 0}}{6}\\1 - {y_I} =  - \dfrac{{2.\left( { - 1} \right) + 20}}{6}\\1 - {z_I} =  - \dfrac{{2.\left( { - 2} \right) + \left( { - 20} \right)}}{6}\end{array} \right. \Rightarrow I\left( {1;4; - 3} \right)$

+) Ta có:

$\begin{array}{l}3M{A^2} + 2M{B^2} + M{C^2} = 3{\left( {\overrightarrow {MI}  + \overrightarrow {IA} } \right)^2} + 2{\left( {\overrightarrow {MI}  + \overrightarrow {IB} } \right)^2} + {\left( {\overrightarrow {MI}  + \overrightarrow {IC} } \right)^2}\\ = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2} + 2.\overrightarrow {MI} .\left( {3\overrightarrow {IA}  + 2\overrightarrow {IB}  + \overrightarrow {IC} } \right) = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2} + 2.\overrightarrow {MI} .\overrightarrow 0 \\ = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2}\end{array}$

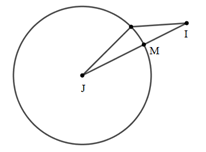
Để tổng trên là nhỏ nhất thì MI nhỏ nhất $ \Rightarrow M$là giao điểm của đoạn thẳng $IJ$ và  mặt cầu $\left( S \right)$.

$\overrightarrow {JI}  = \left( {0;3; - 4} \right)$

$ \Rightarrow $Tọa độ điểm $M$thuộc đoạn IJ có dạng $\left( {1;1 + 3t;1 - 4t} \right),\,\,t \in \left[ {0;1} \right]$

Mặt khác $M \in \left( S \right) \Rightarrow {\left( {1 - 1} \right)^2} + {\left( {1 - \left( {1 + 3t} \right)} \right)^2} + {\left( {1 - \left( {1 - 4t} \right)} \right)^2} = 1$

$ \Leftrightarrow {t^2} = \dfrac{1}{{25}} \Leftrightarrow \left[ \begin{array}{l}t = \dfrac{1}{5}\\t =  - \dfrac{1}{5}\,(L)\end{array} \right. \Leftrightarrow t = \dfrac{1}{5}$  $ \Rightarrow M\left( {1;\dfrac{8}{5};\dfrac{1}{5}} \right) \Rightarrow OM = \dfrac{{3\sqrt {10} }}{5}$.