Câu hỏi:
2 năm trước
Cho ba tia Ox, Oy, Oz đôi một vuông góc với nhau. Gọi C là điểm cố định trên Oz, đặt OC = 1, các điểm A, B thay đổi trên Ox, Oy sao cho $OA + OB = OC$. Giá trị bé nhất của bán kính mặt cầu ngoại tiếp tứ diện OABC là
Trả lời bởi giáo viên
Đáp án đúng: c
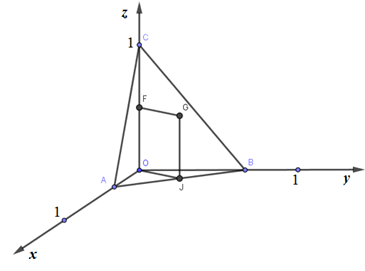
Đặt $A\left( {x;0;0} \right),\,\,B\left( {0;y;0} \right),\,\,\left( {x,y > 0} \right)$
Vì $OA + OB = OC = 1 \Rightarrow x + y = 1$
Gọi J, F lần lượt là trung điểm AB, OC. Kẻ đường thẳng qua F song song OJ, đường thẳng qua J song song OC, 2 đường thẳng này cắt nhau tại G.
$\Delta OAB$ vuông tại O $ \Rightarrow J$ là tâm đường tròn ngoại tiếp tam giác.
$GJ//OC \Rightarrow GJ \bot (OAB) \Rightarrow GO = GA = GB$
$GF//JO,\,\,JO \bot OC \Rightarrow GF \bot OC$, mà F là trung điểm của OC
$ \Rightarrow GF$ là đường trung trực của OC $ \Rightarrow GC = GO$
$ \Rightarrow GO = GA = GB = GC \Rightarrow G$ là tâm mặt cầu ngoại tiếp tứ diện OABC
Bán kính mặt cầu ngoại tiếp tứ diện OABC : $R = OG = FJ = \sqrt {O{F^2} + O{J^2}} = \sqrt {{{\left( {\dfrac{1}{2}} \right)}^2} + O{J^2}} $
Ta có: $OJ = \dfrac{{AB}}{2} = \dfrac{{\sqrt {{x^2} + {y^2}} }}{2} \ge \dfrac{{\sqrt {\dfrac{{{{(x + y)}^2}}}{2}} }}{2} = \dfrac{{\sqrt {\dfrac{{{1^2}}}{2}} }}{2} = \dfrac{{\sqrt 2 }}{4}$$ \Rightarrow R \ge \sqrt {{{\left( {\dfrac{1}{2}} \right)}^2} + {{\left( {\dfrac{{\sqrt 2 }}{4}} \right)}^2}} = \sqrt {\dfrac{3}{8}} \Rightarrow {R_{\min }} = \sqrt {\dfrac{3}{8}} = \dfrac{{\sqrt 6 }}{4}$
Hướng dẫn giải:
Sử dụng phương pháp xác định tâm mặt cầu ngoại tiếp khối chóp.
