Người ta cần chế tạo các món quà lưu niệm bằng đồng có dạng khối chóp tứ giác đều, được mạ vàng bốn mặt bên và có thể tích bằng 49 cm3. Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu cm2? (Kết quả làm tròn đến hàng đơn vị)
Điền số nguyên hoặc phân số dạng a/b
Đáp án:
Đáp án:
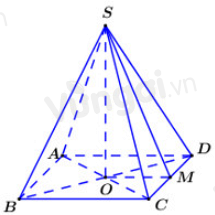
Gọi khối chóp tứ giác đều thỏa mãn yêu cầu bài toán là \(S.ABCD\).
Gọi \(O = AC \cap BD\).
Đặt \(AB = x\,\,\left( {x > 0} \right)\).
\( \Rightarrow {S_{ABCD}} = {x^2}\).
Khi đó \({V_{S.ABCD}} = \dfrac{1}{3}.SO.{S_{ABCD}}\)
\( \Leftrightarrow \dfrac{1}{3}SO.{x^2} = 49\)
\( \Leftrightarrow SO = \dfrac{{147}}{{{x^2}}}\).
Gọi \(M\) là trung điểm của \(CD\). Suy ra \(OM\) là đường trung bình của tam giác \(BCD\).
Khi đó \(OM//BC\) và \(OM = \dfrac{1}{2}BC = \dfrac{x}{2}\).
Ta có \(SM = \sqrt {S{O^2} + O{M^2}} = \sqrt {{{\left( {\dfrac{{147}}{{{x^2}}}} \right)}^2} + {{\left( {\dfrac{x}{2}} \right)}^2}} = \sqrt {\dfrac{{{{147}^2}}}{{{x^4}}} + \dfrac{{{x^2}}}{4}} \)
Ta có \(\left\{ \begin{array}{l}CD \bot OM\,\,\left( {OM//BC} \right)\\CD \bot SO\,\,\left( {SO \bot \left( {ABCD} \right)} \right)\\Trong\,\,\left( {SOM} \right):SO \cap OM = O\end{array} \right.\)
\( \Rightarrow CD \bot \left( {SOM} \right)\).
Mà \(SM \subset \left( {SOM} \right)\).
\( \Rightarrow CD \bot SM\).
Ta có \({S_{SCD}} = \dfrac{1}{2}SM.CD = \dfrac{1}{2}.\sqrt {\dfrac{{{{147}^2}}}{{{x^4}}} + \dfrac{{{x^2}}}{4}} .x = \dfrac{1}{2}.\sqrt {\dfrac{{{{147}^2}}}{{{x^2}}} + \dfrac{{{x^4}}}{4}} \)
Để diện tích mạ vàng nhỏ nhất thì \({S_{SCD}}\) nhỏ nhất.
\( \Leftrightarrow \sqrt {\dfrac{{{{147}^2}}}{{{x^2}}} + \dfrac{{{x^4}}}{4}} \) nhỏ nhất.
Ta có \(\dfrac{{{{147}^2}}}{{{x^2}}} + \dfrac{{{x^4}}}{4} = \dfrac{{10804}}{{{x^2}}} + \dfrac{{10805}}{{{x^2}}} + \dfrac{{{x^4}}}{4} \ge 3.\sqrt[3]{{\dfrac{{10804}}{{{x^2}}}.\dfrac{{10805}}{{{x^2}}}.\dfrac{{{x^4}}}{4}}}\)
\( = 3.\sqrt[3]{{\dfrac{{10804}}{{{x^2}}}.\dfrac{{10805}}{{{x^2}}}.\dfrac{{{x^4}}}{4}}} = 3\sqrt[3]{{29184305}}\) (theo bất đẳng thức Cauchy).
Vậy diện tích mạ vàng nhỏ nhất bằng \(4.{S_{SCD\,\min }} = 4.\dfrac{1}{2}\sqrt {3.\sqrt[3]{{29184305}}} \approx 60,783\) (cm2).
Cho khối chóp tứ giác $S.ABCD.$ Mặt phẳng đi qua trọng tâm các tam giác \(SAB,\;SAC,\;\;SAD\) chia khối chóp này thành hai phần có thể tích là \({V_1}\) và \({V_2}\;\;\left( {{V_1} < {V_2}} \right).\) Tính tỉ lệ \(\dfrac{{{V_1}}}{{{V_2}}}.\)
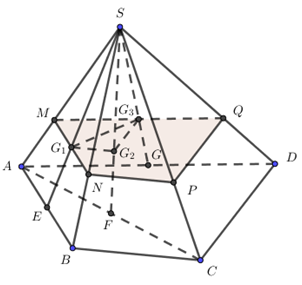
Gọi \({G_1};{G_2};{G_3}\) lần lượt là trực tâm các tam giác SAB, SAC và SAD.
Gọi E, F, G lần lượt là trung điểm của AB, AC và AD ta có:
\(\dfrac{{S{G_1}}}{{SE}} = \dfrac{{S{G_2}}}{{SF}} = \dfrac{{S{G_3}}}{{SG}} = \dfrac{2}{3} \Rightarrow {G_1}{G_2}//EF;\,\,{G_2}{G_3}//FG \Rightarrow \left( {{G_1}{G_2}{G_3}} \right)//\left( {EFG} \right)\)
Hay \(\left( {{G_1}{G_2}{G_3}} \right)//\left( {ABC} \right)\)
Qua \({G_1}\) kẻ MN // AB \(\left( {M \in SA;N \in SB} \right)\).
Qua \({G_3}\) kẻ \(MQ//AD\,\,\left( {Q \in SD} \right)\)
Qua N kẻ \(NP//BC\,\,\left( {N \in SC} \right)\)
\( \Rightarrow \) Thiết diện của khối chóp cắt bởi mặt phẳng \(\left( {{G_1}{G_2}{G_3}} \right)\) là \(\left( {MNPQ} \right)\), chia khối chóp thành hai phần : \(S.MNPQ\) và \(MNPQ.ABCD\).
Áp dụng định lí Ta-lét ta tính được \(\dfrac{{SM}}{{SA}} = \dfrac{{SN}}{{SB}} = \dfrac{{SP}}{{SC}} = \dfrac{{SQ}}{{SD}} = \dfrac{2}{3}\).
Ta có \(\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}} = \dfrac{2}{3}.\dfrac{2}{3}.\dfrac{2}{3} = \dfrac{8}{{27}} \Rightarrow {V_{S.MNP}} = \dfrac{8}{{27}}{V_{S.ABC}}\)
\(\dfrac{{{V_{S.MPQ}}}}{{{V_{S.ACD}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SP}}{{SC}}.\dfrac{{SQ}}{{SD}} = \dfrac{2}{3}.\dfrac{2}{3}.\dfrac{2}{3} = \dfrac{8}{{27}} \Rightarrow {V_{S.MPQ}} = \dfrac{8}{{27}}{V_{S.ACD}}\)
\(\begin{array}{l} \Rightarrow {V_{S.MNPQ}} = {V_{S.MNP}} + {V_{S.MPQ}} = \dfrac{8}{{27}}\left( {{V_{S.ABC}} + {V_{S.ACD}}} \right) = \dfrac{8}{{27}}{V_{S.ABCD}}\\ \Rightarrow {V_1} = \dfrac{8}{{27}}{V_{S.ABCD}};\,\,{V_2} = \dfrac{{19}}{{27}}{V_{S.ABCD}}\\ \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{8}{{19}}\end{array}\)
Xét khối tứ diện $ABCD$ có cạnh $AD, BC$ thỏa mãn $A{B^2} + C{D^2} = 18$ và các cạnh còn lại đều bằng $5.$ Biết thể tích của khối tứ diện $ABCD $ đạt giá trị lớn nhất có dạng ${V_{\max }} = \dfrac{{x\sqrt y }}{4};\,\,x,y \in {N^*};\,\,(x;y) = 1$. Khi đó, $x,\,y$ thỏa mãn bất đẳng thức nào dưới đây?
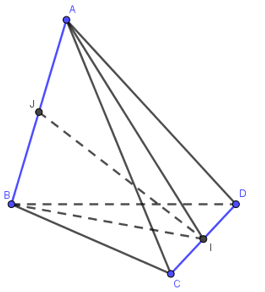
Gọi $I, J$ lần lượt là trung điểm $CD, AB$; độ dài các đoạn $AB = a,\,\,CD = b,\,\,a,b > 0,\,\,{a^2} + {b^2} = 18$
Tam giác $ACD$ và tam giác $ BCD$ cân tại $A, B$
$ \Rightarrow AI \bot CD,\,\,BI \bot CD \Rightarrow CD \bot (ABI)$
$ \Rightarrow {V_{ABCD}} = {V_{D.ABI}} + {V_{C.ABI}} $ $= \dfrac{1}{3}.DI.{S_{ABI}} + \dfrac{1}{3}.IC.{S_{ABI}} = \dfrac{1}{3}.CD.{S_{ABI}}$ (*)
Tam giác $AID$ vuông tại $I $ $ \Rightarrow AI = \sqrt {A{D^2} - I{D^2}} = \sqrt {{5^2} - {{\left( {\dfrac{b}{2}} \right)}^2}} = \sqrt {25 - \dfrac{{{b^2}}}{4}} $
Dễ dàng chứng minh $\Delta ACD = \Delta BCD\,\,(c.c.c) \Rightarrow IA = IB$ (Chiều cao tương ứng bằng nhau)
$ \Rightarrow \Delta IAB$ cân tại $I $ $ \Rightarrow IJ \bot AB$
Tam giác $AIJ$ vuông tại $J $ $ \Rightarrow IJ = \sqrt {A{I^2} - A\,{J^2}} = \sqrt {25 - \dfrac{{{b^2}}}{4} - \dfrac{{{a^2}}}{4}} = \sqrt {25 - \dfrac{{{b^2} + {a^2}}}{4}} = \sqrt {25 - \dfrac{{18}}{4}} = \dfrac{{\sqrt {82} }}{2}$
Diện tích tam giác $IAB: $ ${S_{IAB}} = \dfrac{1}{2}.AB.IJ = \dfrac{1}{2}.a.\dfrac{{\sqrt {82} }}{2} = \dfrac{{a\sqrt {82} }}{4}$.
Thay vào (*):
$\begin{array}{l}{V_{ABCD}} = \dfrac{1}{3}.b.\dfrac{{a\sqrt {82} }}{4} = \dfrac{{ab\sqrt {82} }}{{12}}\mathop \le \limits^{Co\,si} \dfrac{{\sqrt {82} }}{{12}}.\dfrac{{{a^2} + {b^2}}}{2} = \dfrac{{\sqrt {82} }}{{12}}.\dfrac{{18}}{2} = \dfrac{{3\sqrt {82} }}{4} = \dfrac{{x\sqrt[{}]{y}}}{4};\,\,x,y \in {N^*};\,\,(x;y) = 1\\ \Rightarrow x = 3,\,\,y = 82\end{array}$
Kiểm tra các biểu thức của từng phương án, ta thấy phương án A là đúng.
Cho hình hộp đứng $ABCD.A’B’C’D’$ có đáy $ABCD$ là hình thoi cạnh $a$ và $\widehat {BAD} = {60^0}$, $AB’$ hợp với đáy $(ABCD)$ một góc ${30^0}$. Thể tích của khối hộp là
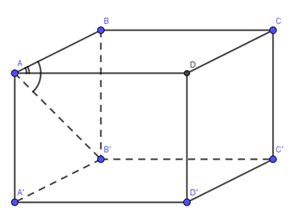
$ABCD.A’B’C’D’$ là hình hộp đứng
$ \Rightarrow BB' \bot (ABCD) \Rightarrow \left( {\widehat {AB',(ABCD)}} \right) = \left( {\widehat {AB';AB}} \right) = \widehat {BAB'} = {30^0}$
Tam giác $ABB’$ vuông tại $B$ $ \Rightarrow \tan \widehat {BAB'} = \dfrac{{BB'}}{{AB}}$
$ \Rightarrow BB' = AB.\tan {30^0} = \dfrac{a}{{\sqrt 3 }}$
Tam giác $ABD $ có: $AB = AD = a,$ $\widehat {BAD} = {60^0} \Rightarrow $ Tam giác $ABD$ đều, có cạnh đều bằng $a.$
$ \Rightarrow {S_{ABD}} = \dfrac{{{a^2}\sqrt 3 }}{4} \Rightarrow {S_{ABCD}} = 2\,{S_{ABD}} = 2.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^2}\sqrt 3 }}{2}$
Thể tích khối hộp $ABCD.A’B’C’D’$: $V = {S_{ABCD}}.BB' = \dfrac{{{a^2}\sqrt 3 }}{2}.\dfrac{a}{{\sqrt 3 }} = \dfrac{{{a^3}}}{2}$.
Cho khối chóp $S.ABC$ có điểm $M$ và $N$ lần lượt nằm trên các cạnh $SA$ và $SB$ sao cho $\dfrac{{SM}}{{SA}} = \dfrac{1}{3},\,\dfrac{{SN}}{{SB}} = \dfrac{2}{3}$. Mặt phẳng $\left( \alpha \right)$ qua hai điểm $M, N$ và song song $SC$ chia khối chóp thành $2$ khối đa diện. Tính tỉ số thể tích của khối đa diện có thể tích lớn hơn so với thể tích khối chóp $S.ABC.$
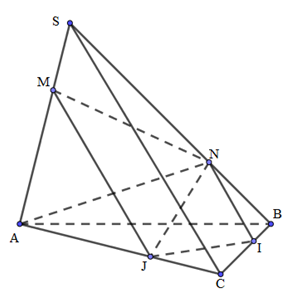
Trong mặt phẳng \(\left( {SBC} \right)\) : kẻ $NI//SC,I \in BC$ .
Trong mặt phẳng $\left( {SAC} \right)$ : kẻ $MJ//SC,J \in AC$ .
\( \Rightarrow \) Thiết diện của hình chóp cắt bởi $\left( \alpha \right)$ là $MNIJ$.
Ta tính tỉ số thế tích của khối đa diện $MNBIJA$ với khối chóp $S.ABC $:
Ta có:
$\begin{array}{l}\dfrac{{{V_{N.MAJ}}}}{{{V_{S.ABC}}}} = \dfrac{{\dfrac{1}{3}.d(N,\,(SAC)).\,{S_{AMJ}}}}{{\dfrac{1}{3}.d(B,(SAC)).{S_{SAC}}}} = \dfrac{{d(N,\,(SAC))}}{{d(B,\,(SAC))}}.\dfrac{{{S_{AMJ}}}}{{{S_{SAC}}}}\\ = \dfrac{{SN}}{{BS}}.\dfrac{{AM}}{{SA}}.\dfrac{{AJ}}{{AC}} = \dfrac{2}{3}.\dfrac{2}{3}.\dfrac{2}{3} = \dfrac{8}{{27}} \Rightarrow {V_{N.MAJ}} = \dfrac{8}{{27}}{V_{S.ABC}}\,\,(1)\end{array}$
$\dfrac{{{V_{N.ABIJ}}}}{{{V_{S.ABC}}}} = \dfrac{{\dfrac{1}{3}.d(N,(ABC)).{S_{ABIJ}}}}{{\dfrac{1}{3}.d(S,(ABC)).{S_{ABC}}}} = \dfrac{{d(N,(ABC))}}{{d(S,(ABC))}}.\dfrac{{{S_{ABIJ}}}}{{{S_{ABC}}}} = \dfrac{{NB}}{{SB}}.\dfrac{{{S_{ABIJ}}}}{{{S_{ABC}}}} = \dfrac{1}{3}.\dfrac{7}{9} = \dfrac{7}{{27}}$ (vì $\dfrac{{{S_{CIJ}}}}{{{S_{ABC}}}} = \dfrac{{IC}}{{BC}}.\dfrac{{JC}}{{AC}} = \dfrac{2}{3}.\dfrac{1}{3} = \dfrac{2}{9}$ ).
$ \Rightarrow {V_{N.ABIJ}} = \dfrac{7}{{27}}{V_{S.ABC}}\,\,(2)$
Từ (1), (2) suy ra ${V_{N.AMJ}} + {V_{N.ABIJ}} = \left( {\dfrac{8}{{27}} + \dfrac{7}{{27}}} \right){V_{S.ABC}} \Leftrightarrow {V_{MNBIJA}} = \dfrac{5}{9}{V_{S.ABC}} \Rightarrow \dfrac{{{V_{MNBIJA}}}}{{{V_{S.ABC}}}} = \dfrac{5}{9}$
Cho hình chóp tứ giác đều $S.ABCD,$ đường cao $SO.$ Biết rằng trong các thiết diện của hình chóp cắt bởi các mặt phẳng chứa $SO,$ thiết diện có diện tích lớn nhất là tam giác đều cạnh bằng $a,$ tính thể tích khối chóp đã cho.
Gọi $\left( \alpha \right)$ là mặt phẳng chứa $SO,$ cắt mặt đáy \(\left( {ABCD} \right)\) theo giao tuyến là đường thẳng \(MN\) với \(M,N\) thuộc các cạnh của hình vuông \(ABCD\).
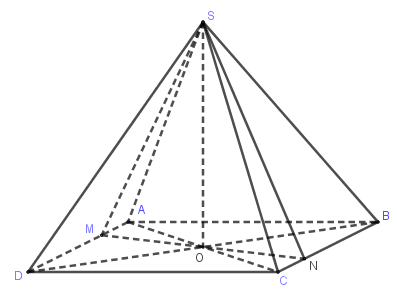
Không mất tính tổng quát ta giả sử \(MN\) như hình vẽ.
Ta có : \({S_{SMN}} = \dfrac{1}{2}SO.MN \le \dfrac{1}{2}SO.AC = {S_{SAC}} = const\)
Do đó \({S_{SMN}}\) đạt giá trị lớn nhất bằng \({S_{SAC}}\) khi \(MN = AC=BD\).
Mà tam giác $SMN $ đều cạnh $a$ nên $AC=BD=a$
\(\Rightarrow {S_{ABCD}} = \dfrac{1}{2}AC.BD = \dfrac{{{a^2}}}{2}\) và \(SO = \dfrac{{a\sqrt 3 }}{2}\).
Thể tích \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2}.\dfrac{1}{2}{a^2} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\)
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $B$, $AB = a.$ Cạnh bên $SA = a$ và vuông góc với đáy. Mặt phẳng qua $A$ vuông góc với $SC$ cắt hình chóp theo một thiết diện. Tính diện tích thiết diện đó.
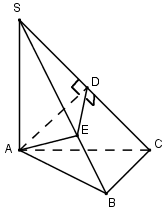
Trong $(SAC)$ qua $A$ kẻ \(AD \bot SC\,\,\left( {D \in SC} \right)\), trong $(SBC)$ qua $D$ kẻ \(DE \bot SC\,\,\left( {E \in SB} \right)\). Khi đó mặt phẳng qua $A$ vuông góc với $SC $ cắt hình chóp theo một thiết diện là tam giác $ADE.$
Tam giác $ABC$ vuông cân tại $B$ nên \(AC = AB\sqrt 2 = a\sqrt 2 \)
Xét tam giác vuông $SAC:$ \(\dfrac{{SD}}{{SC}} = \dfrac{{S{A^2}}}{{S{C^2}}} = \dfrac{{S{A^2}}}{{S{A^2} + A{C^2}}} = \dfrac{1}{3}\)
Xét tam giác vuông $SAB:$ \(\dfrac{{SE}}{{SB}} = \dfrac{{S{A^2}}}{{S{B^2}}} = \dfrac{{S{A^2}}}{{S{A^2} + A{B^2}}} = \dfrac{1}{2}\)
$ \Rightarrow \dfrac{{{V_{S.ADE}}}}{{{V_{S.ACB}}}} = \dfrac{{SD}}{{SC}}.\dfrac{{SE}}{{SB}} = \dfrac{1}{6} \Rightarrow {V_{S.ADE}} = \dfrac{1}{6}{V_{S.ACB}} = \dfrac{1}{6}.\dfrac{1}{3}SA.\dfrac{1}{2}BA.BC = \dfrac{{{a^3}}}{{36}}$
Mà \(SC \bot \left( {ADE} \right) \Rightarrow {V_{S.ADE}} = \dfrac{1}{3}SD.{S_{ADE}} \Rightarrow {S_{ADE}} = \dfrac{{3{V_{S.ADE}}}}{{SD}} = \dfrac{{3{V_{S.ADE}}}}{{\dfrac{1}{3}SC}} = \dfrac{{9{V_{S.ADE}}}}{{\sqrt {S{A^2} + A{C^2}} }} = \dfrac{{9.\dfrac{{{a^3}}}{{36}}}}{{\sqrt {{a^2} + 2{a^2}} }} = \dfrac{{{a^2}\sqrt 3 }}{{12}}\)
Cho hình hộp $ABCD.A’B’C’D’$ có tất cả các cạnh bằng $a,$ hình chiếu vuông góc của $A’$ lên mặt phẳng $(ABCD)$ nằm trong tứ giác $ABCD,$ các cạnh xuất phát từ đỉnh $A$ của hình hộp tạo với nhau một góc $60^0.$ Tính thể tích khối hộp $ABCD.A’B’C’D’.$
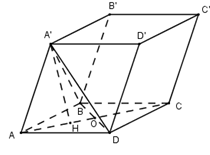
Gọi $H$ là chân đường vuông góc hạ từ đỉnh $A’$ lên $(ABCD).$
Vì $\widehat {A'AB} = \widehat {A'AD} = \widehat {BAD} = {60^0} \Rightarrow $ Các tam giác $AA’B, ABD$ và $AA’D$ là các tam giác đều cạnh $a$ \( \Rightarrow A'A = A'B' = A'D = a \)
\(\Rightarrow \) Hình chóp $A’.ABD$ có các cạnh bên bằng nhau nên $H$ là tâm của tam giác đều $ABD.$
Dễ dàng tính được \(AH = \dfrac{2}{3}AO = \dfrac{2}{3}\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
Xét tam giác vuông $AA’H$ có \(A'H = \sqrt {A'{A^2} - A{H^2}} = \dfrac{{a\sqrt 6 }}{3}\)
\(\begin{array}{l}{S_{ABCD}} = 2{S_{ABD}} = 2\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^2}\sqrt 3 }}{2}\\ \Rightarrow {V_{ABCD.A'B'C'D'}} = \dfrac{{a\sqrt 6 }}{3}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 2 }}{2}\end{array}\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và \(SA = SB = SC = a\). Thể tích lớn nhất của khối chóp \(S.ABCD\) là:
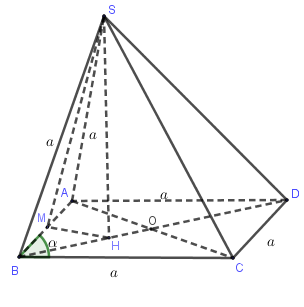
Gọi \(M\) là trung điểm của \(AB\), \(O\) là giao điểm của \(AC\) và \(BD\).
Qua \(M\) kẻ đường thẳng vuông góc với \(AB\) và cắt \(BO\) tại\(H\).
Khi đó \(H\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).
Vì \(SA = SB = SC\) nên \(SH \bot \left( {ABC} \right)\).
Đặt \(\widehat {ABC} = \alpha \) ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos \alpha \\ = {a^2} + {a^2} - 2{a^2}\cos \alpha = 2{a^2}\left( {1 - \cos \alpha } \right)\\ \Rightarrow A{O^2} = \dfrac{{A{C^2}}}{4} = \dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{2}\end{array}\)
Tam giác \(AOB\) vuông tại \(O\) nên:\(O{B^2} = A{B^2} - A{O^2} = {a^2} - \dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{2} = \dfrac{{{a^2}\left( {1 + \cos \alpha } \right)}}{2}\)
Xét tam giác \(\Delta BHM \sim \Delta BAO\left( {g.g} \right)\) nên \(\dfrac{{MH}}{{AO}} = \dfrac{{BM}}{{BO}} \Rightarrow MH = \dfrac{{AO.BM}}{{BO}}\)
\( \Rightarrow M{H^2} = \dfrac{{A{O^2}.B{M^2}}}{{B{O^2}}} = \dfrac{{\dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{2}.\dfrac{{{a^2}}}{4}}}{{\dfrac{{{a^2}\left( {1 + \cos \alpha } \right)}}{2}}} = \dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{{4\left( {1 + \cos \alpha } \right)}}\)
Tam giác \(SMH\) vuông tại \(H\) có \(S{H^2} = S{M^2} - M{H^2} = \dfrac{{3{a^2}}}{4} - \dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{{4\left( {1 + \cos \alpha } \right)}} = \dfrac{{{a^2}}}{4}\left( {3 - \dfrac{{1 - \cos \alpha }}{{1 + \cos \alpha }}} \right) = \dfrac{{{a^2}}}{4}.\dfrac{{2 + 4\cos \alpha }}{{1 + \cos \alpha }} = \dfrac{{{a^2}\left( {1 + 2\cos \alpha } \right)}}{{2\left( {1 + \cos \alpha } \right)}}\)
\({S_{ABCD}} = 2{S_{ABC}} = BO.AC \Rightarrow S_{ABCD}^2 = B{O^2}.A{C^2} = \dfrac{{{a^2}\left( {1 + \cos \alpha } \right)}}{2}.2{a^2}\left( {1 - \cos \alpha } \right) = {a^4}\left( {1 + \cos \alpha } \right)\left( {1 - \cos \alpha } \right)\)
\(\begin{array}{l} \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}{S_{ABCD}}.SH\\ \Rightarrow V_{S.ABCD}^2 = \dfrac{1}{9}S_{ABCD}^2.S{H^2} = \dfrac{1}{9}{a^4}\left( {1 + \cos \alpha } \right)\left( {1 - \cos \alpha } \right).\dfrac{{{a^2}\left( {1 + 2\cos \alpha } \right)}}{{2\left( {1 + \cos \alpha } \right)}} = \dfrac{{{a^6}\left( {1 - \cos \alpha } \right)\left( {1 + 2\cos \alpha } \right)}}{{18}}\end{array}\)
Đặt \(t = \cos \alpha \left( {t \in \left[ { - 1;1} \right]} \right)\) và xét hàm \(f\left( t \right) = \left( {1 - t} \right)\left( {1 + 2t} \right) = - 2{t^2} + t + 1\) trên \(\left[ { - 1;1} \right]\) có:
Hàm bậc hai \(f\left( t \right) = - 2{t^2} + t + 1\) có đồ thị là parabol với bề lõm hướng xuống dưới.
Do đó nó đạt GTLN tại \(t = \dfrac{1}{4}\) và \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} f\left( t \right) = f\left( {\dfrac{1}{4}} \right) = \dfrac{9}{8}\).
Khi đó \(V_{\max }^2 = \dfrac{{{a^6}}}{{18}}.\dfrac{9}{8} = \dfrac{{{a^6}}}{{16}} \Rightarrow V = \dfrac{{{a^3}}}{4}\)
Cho hình chóp \(S.ABC\) có \(AB = 3,BC = 4,AC = 5\). Tính thể tích khối chóp \(S.ABC\) biết rằng cắc mặt bên tạo với đáy một góc \({30^0}\) và hình chiếu vuông góc của \(S\) trên \(\left( {ABC} \right)\) nằm trong tam giác \(ABC\)
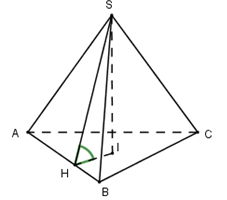
Gọi $I$ là tâm đường tròn nội tiếp \(\Delta ABC \Rightarrow SI \bot \left( {ABC} \right)\)
Dễ thấy \(\Delta ABC\) vuông tại \(B \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}BA.BC = \dfrac{1}{2}.3.4 = 6\), nửa chu vi \(\Delta ABC:\,\,p = \dfrac{{3 + 4 + 5}}{2} = 6\)
Gọi \(H\) là hình chiếu của \(I\) trên cạnh \(AB\) ta có
\(S = p.r \Rightarrow r = \dfrac{S}{p} = 1\), với $r$ là tâm đường tròn nội tiếp \(\Delta ABC \Rightarrow IH = 1\).
\(\left\{ \begin{array}{l}AB \bot IH\\AB \bot SI\end{array} \right. \Rightarrow AB \bot \left( {SHI} \right) \Rightarrow AB \bot SH \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SH;IH} \right)} = \widehat {SHI} = {30^0}\)
Xét tam giác vuông \(SHI\) có \(SI = HI.\tan 30 = \dfrac{1}{{\sqrt 3 }}\)
Vậy \({V_{S.ABC}} = \dfrac{1}{3}SI.{S_{\Delta ABC}} = \dfrac{1}{3}.\dfrac{1}{{\sqrt 3 }}.6 = \dfrac{{2\sqrt 3 }}{3}\)
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(E,F\) lần lượt là trung điểm của \(B'C'\) và \(C'D'\). Mặt phẳng \(\left( {AEF} \right)\) chia hình hộp thành hai hình đa diện \(\left( H \right)\) và \(\left( {H'} \right)\) trong đó \(\left( H \right)\) là hình đa diện chứa đỉnh \(A'\). Tính tỉ số thể tích đa diện \(\left( H \right)\) và thể tích hình đa diện \(\left( {H'} \right)\).
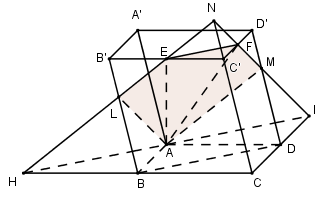
Mặt phẳng \(\left( {AEF} \right)\) chứa \(EF//BD \subset \left( {ABCD} \right)\)
\( \Rightarrow \) Giao tuyến của \(\left( {AEF} \right)\) và \(\left( {ABCD} \right)\) là đường thẳng đi qua \(A\) và song song với \(EF\)
Trong \(\left( {ABCD} \right)\) qua \(A\) kẻ \(HI//BD\,\,\left( {H \in BC,I \in CD} \right)\)
Trong \(\left( {BCC'B'} \right)\) gọi \(L = EH \cap BB'\), trong \(\left( {CDD'C'} \right)\) gọi \(M = FI \cap DD'\), khi đó \(\left( {AEF} \right) \equiv \left( {ALEFM} \right)\)
Ta có : \(\left\{ \begin{array}{l}\left( {AEF} \right) \cap \left( {BCC'B'} \right) = HE\\\left( {AEF} \right) \cap \left( {CDD'C'} \right) = FI\\\left( {BCC'B'} \right) \cap \left( {CDD'C'} \right) = CC'\end{array} \right. \)
\(\Rightarrow HE,FI,CC'\) đồng quy tại \(N\).
Ta có : \({V_{H'}} = {V_{N.CIH}} - {V_{N.EFC'}} - {V_{L.ABH}} - {V_{M.ADI}}\)
Ta dễ dàng chứng minh được \(B,D\) lần lượt là trung điểm của \(CH,CI \Rightarrow BD = \dfrac{1}{2}HI \Rightarrow EF = \dfrac{1}{2}BD = \dfrac{1}{4}HI\)
\( \Rightarrow \Delta C'EF\) đồng dạng với \(\Delta CIH\) theo tỉ số đồng dạng \(k = \dfrac{1}{4} \Rightarrow \dfrac{{{S_{\Delta C'EF}}}}{{{S_{\Delta CIH}}}} = \dfrac{1}{{16}}\)
$\begin{array}{l}\dfrac{{NC'}}{{NC}} = \dfrac{{EC'}}{{HC}} = \dfrac{1}{4} \Rightarrow \dfrac{{d\left( {N';\left( {C'EF} \right)} \right)}}{{d\left( {N;\left( {CIH} \right)} \right)}} = \dfrac{1}{4}\\ \Rightarrow {V_{N.EFC'}} = \dfrac{1}{{16}}.\dfrac{1}{4}{V_{N.CIH}} = \dfrac{1}{{64}}{V_{N.CIH}}\\{V_{LABH}} = {V_{M.ADI}} = \dfrac{1}{2}.\dfrac{1}{4}{V_{N.CIH}} = \dfrac{1}{8}{V_{N.CIH}}\\ \Rightarrow {V_{H'}} = {V_{N.CIH}} - {V_{N.EFC'}} - {V_{L.ABH}} - {V_{M.ADI}} = \dfrac{{47}}{{64}}{V_{N.CIH}}\end{array}$
Ta có :
\(\begin{array}{l}\dfrac{{CC'}}{{NC}} = \dfrac{3}{4},\dfrac{{{S_{ABCD}}}}{{{S_{CIH}}}} = \dfrac{1}{2} \Rightarrow \dfrac{{{V_{ABCD.A'B'C'D'}}}}{{{V_{S.CIH}}}} = \dfrac{{d\left( {C';\left( {ABCD} \right)} \right).{S_{ABCD}}}}{{\dfrac{1}{3}d\left( {N;\left( {CIH} \right)} \right).{S_{CIH}}}} = 3.\dfrac{{CC'}}{{NC}}.\dfrac{{{S_{ABCD}}}}{{{S_{CIH}}}} = 3.\dfrac{3}{4}.\dfrac{1}{2} = \dfrac{9}{8}\\ \Rightarrow {V_{S.CIH}} = \dfrac{8}{9}{V_{ABCD.A'B'C'D'}}\\ \Rightarrow {V_{H'}} = \dfrac{{47}}{{64}}{V_{N.CIH}} = \dfrac{{47}}{{72}}{V_{ABCD.A'B'C'D'}}\\ \Rightarrow {V_H} = \dfrac{{25}}{{72}}{V_{ABCD.A'B'C'D'}}\\ \Rightarrow \dfrac{{{V_H}}}{{{V_{H'}}}} = \dfrac{{25}}{{47}}\end{array}\)
Cho hình chóp tứ giác đều có mặt bên hợp với đáy một góc $45^0$ và khoảng cách từ chân đường cao đến mặt bên bằng \(a\). Tính thể tích của khối chóp đó.
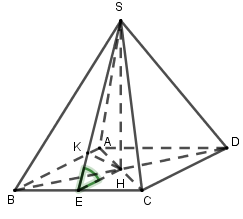
Gọi \(H\) là tâm tam hình vuông \(ABCD \Rightarrow SH \bot \left( {ABCD} \right)\)
Gọi \(E\) là trung điểm của \(BC\) ta có : \(\left\{ \begin{array}{l}BC \bot AE\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SAE} \right) \Rightarrow BC \bot SE\)
\( \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SE;AE} \right)} = \widehat {SEA} = {45^0}\)
Trong \(\left( {SAE} \right)\) kẻ \(HK \bot SE \Rightarrow HK \bot \left( {SBC} \right) \Rightarrow HK = a\)
\(\begin{array}{l} \Rightarrow HE = \dfrac{{HK}}{{\cos 45}} = a\sqrt 2 \\ \Rightarrow AB = 2HE = 2a\sqrt 2 \Rightarrow {S_{ABCD}} = 8{a^2}\\SH = HE.\tan 45 = a\sqrt 2 \\ \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}.a\sqrt 2 .8{a^2} = \dfrac{{8{a^3}\sqrt 2 }}{3}\end{array}\)
Người ta cần chế tạo các món quà lưu niệm bằng đồng có dạng khối chóp tứ giác đều, được mạ vàng bốn mặt bên và có thể tích bằng \(16 cm^3.\) Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu \(cm^2\)? (Kết quả làm tròn đến hàng đơn vị.)
Đáp án
$cm^3$
Đáp án
$cm^3$
Bước 1: Giả sử chóp tứ giác đều là \(S.ABCD\). Gọi \(O = AC \cap BD\), đặt \(AB = x\,\,\left( {x > 0} \right)\), tính \(SO\) theo \(x\).
Giả sử chóp tứ giác đều là \(S.ABCD\). Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\).
Đặt \(AB = x\,\,\left( {x > 0} \right)\) ta có \({S_{ABCD}} = {x^2}\) \( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}SO.{x^2} = 16 \Leftrightarrow SO = \dfrac{{48}}{{{x^2}}}\).
Bước 2: Gọi M là trung điểm của CD. Tính \(SM\) theo \(x\), từ đó tính \({S_{\Delta SCD}}\) theo \(x\).
Gọi M là trung điểm của CD ta có \(\left\{ \begin{array}{l}CD \bot OM\\CD \bot SO\end{array} \right. \Rightarrow CD \bot \left( {SOM} \right) \Rightarrow CD \bot SM\).
Ta có \(OM = \dfrac{1}{2}AD = \dfrac{1}{2}AB = \dfrac{x}{2}\), áp dụng định lí Pytago ta có: \(SM = \sqrt {S{O^2} + O{M^2}} = \sqrt {{{\left( {\dfrac{{48}}{{{x^2}}}} \right)}^2} + \dfrac{{{x^2}}}{4}} \).
\( \Rightarrow {S_{\Delta SCD}} = \dfrac{1}{2}SM.CD = \dfrac{1}{2}\sqrt {{{\left( {\dfrac{{48}}{{{x^2}}}} \right)}^2} + \dfrac{{{x^2}}}{4}} .x = \dfrac{1}{2}\sqrt {\dfrac{{{{48}^2}}}{{{x^2}}} + \dfrac{{{x^4}}}{4}} \)
Bước 3: Tìm GTNN của diện tích mạ vàng
Để diện tích mạ vàng nhỏ nhất thì \({S_{\Delta SCD}}\) nhỏ nhất \( \Rightarrow \dfrac{{{{48}^2}}}{{{x^2}}} + \dfrac{{{x^4}}}{4}\) đạt giá trị nhỏ nhất.
Ta có \(\dfrac{{{{48}^2}}}{{{x^2}}} + \dfrac{{{x^4}}}{4} = \dfrac{{1152}}{{{x^2}}} + \dfrac{{1152}}{{{x^2}}} + \dfrac{{{x^4}}}{4} \ge 3\sqrt[3]{{\dfrac{{1152}}{{{x^2}}}.\dfrac{{1152}}{{{x^2}}} . \dfrac{{{x^4}}}{4}}} \)\(\ge 3.\sqrt[3]{331776}\) (BĐT Cô-si).
Vậy diện tích mạ vàng nhỏ nhất là \(4.3.\sqrt[3]{331776}\approx 831\,c{m^3}\).
Khi xây nhà, cô Ngọc cần xây một bể đựng nước mưa có thể tích \(V = 6{m^3}\) dạng hình hộp chữ nhật với chiều dài gấp ba lần chiều rộng, đáy và nắp và các mặt xung quanh đều được đổ bê tông cốt thép. Phần nắp bể để hở một khoảng hình vuông có diện tích bằng \(\dfrac{2}{9}\) diện tích nắp bể. Biết rằng chi phí cho \(1{m^2}\) bê tông cốt thép là \(1.000.000d\). Tính chi phí thấp nhất mà cô Ngọc phải trả khi xây bể (làm tròn đến hàng trăm nghìn và các chữ số viết liền)?
Đáp án
VNĐ
Đáp án
VNĐ
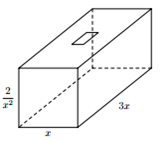
Bước 1: Gọi \(x\left( m \right),\,\,3x\left( m \right)\) lần lượt là chiều rộng, chiều dài của bể. Tính chiều cao của bể.
Gọi \(x\left( m \right),\,\,3x\left( m \right)\) lần lượt là chiều rộng, chiều dài của bể, \(h\) là chiều cao của bể.
Theo bài ra ta có: \(V = x.3x.h = 6 \Rightarrow h = \dfrac{6}{{3{x^2}}} = \dfrac{2}{{{x^2}}}\,\,\left( m \right)\).
Bước 2: Tính tổng diện tích các mặt làm bê tông.
Khi đó tổng diện tích các mặt bể được làm bê tông là:
\(2x.\dfrac{2}{{{x^2}}} + 2.3x.\dfrac{2}{{{x^2}}} + 2x.3x - x.3x.\dfrac{2}{9} = \dfrac{{16{x^2}}}{3} + \dfrac{{16}}{x}\)
Bước 3: Sử dụng BĐT Cô-si cho 3 số dương để tính số tiền ít nhất cần tìm
Áp dụng BĐT Cô-si ta có:
\(\dfrac{{16{x^2}}}{3} + \dfrac{{16}}{x} = \dfrac{{16{x^2}}}{3} + \dfrac{8}{x} + \dfrac{8}{x} \ge 3\sqrt[3]{{\dfrac{{16{x^2}}}{3}.\dfrac{8}{x}.\dfrac{8}{x}}} = 8\sqrt[3]{{18}}\)
Dấu “=” xảy ra khi \(\dfrac{{16{x^2}}}{3} = \dfrac{8}{x} \Leftrightarrow x = \sqrt[3]{{\dfrac{3}{2}}}\).
Vậy số tiền ít nhất mà cô Ngọc cần bỏ ra là \(8\sqrt [3]{18} {.10^6} \approx 21.000.000d\).
