Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh $a$ và $SA = SB = SC = a$. Thể tích lớn nhất của khối chóp $S.ABCD$ là:

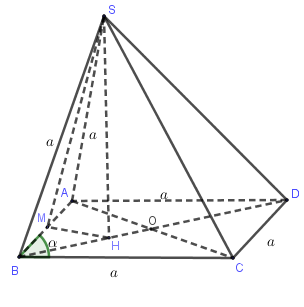
Gọi $M$ là trung điểm của $AB$, $O$ là giao điểm của $AC$ và $BD$.

Qua $M$ kẻ đường thẳng vuông góc với $AB$ và cắt $BO$ tại$H$.

Khi đó $H$ là tâm đường tròn ngoại tiếp tam giác $ABC$.

Vì $SA = SB = SC$ nên $SH \bot \left( {ABC} \right)$.

Đặt $\widehat {ABC} = \alpha$ ta có:

$\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos \alpha \\ = {a^2} + {a^2} - 2{a^2}\cos \alpha  = 2{a^2}\left( {1 - \cos \alpha } \right)\\ \Rightarrow A{O^2} = \dfrac{{A{C^2}}}{4} = \dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{2}\end{array}$

Tam giác $AOB$ vuông tại $O$ nên:$O{B^2} = A{B^2} - A{O^2} = {a^2} - \dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{2} = \dfrac{{{a^2}\left( {1 + \cos \alpha } \right)}}{2}$

Xét tam giác $\Delta BHM \sim \Delta BAO\left( {g.g} \right)$ nên $\dfrac{{MH}}{{AO}} = \dfrac{{BM}}{{BO}} \Rightarrow MH = \dfrac{{AO.BM}}{{BO}}$

$\Rightarrow M{H^2} = \dfrac{{A{O^2}.B{M^2}}}{{B{O^2}}} = \dfrac{{\dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{2}.\dfrac{{{a^2}}}{4}}}{{\dfrac{{{a^2}\left( {1 + \cos \alpha } \right)}}{2}}} = \dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{{4\left( {1 + \cos \alpha } \right)}}$

Tam giác $SMH$ vuông tại $H$ có $S{H^2} = S{M^2} - M{H^2} = \dfrac{{3{a^2}}}{4} - \dfrac{{{a^2}\left( {1 - \cos \alpha } \right)}}{{4\left( {1 + \cos \alpha } \right)}} = \dfrac{{{a^2}}}{4}\left( {3 - \dfrac{{1 - \cos \alpha }}{{1 + \cos \alpha }}} \right) = \dfrac{{{a^2}}}{4}.\dfrac{{2 + 4\cos \alpha }}{{1 + \cos \alpha }} = \dfrac{{{a^2}\left( {1 + 2\cos \alpha } \right)}}{{2\left( {1 + \cos \alpha } \right)}}$

${S_{ABCD}} = 2{S_{ABC}} = BO.AC \Rightarrow S_{ABCD}^2 = B{O^2}.A{C^2} = \dfrac{{{a^2}\left( {1 + \cos \alpha } \right)}}{2}.2{a^2}\left( {1 - \cos \alpha } \right) = {a^4}\left( {1 + \cos \alpha } \right)\left( {1 - \cos \alpha } \right)$

$\begin{array}{l} \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}{S_{ABCD}}.SH\\ \Rightarrow V_{S.ABCD}^2 = \dfrac{1}{9}S_{ABCD}^2.S{H^2} = \dfrac{1}{9}{a^4}\left( {1 + \cos \alpha } \right)\left( {1 - \cos \alpha } \right).\dfrac{{{a^2}\left( {1 + 2\cos \alpha } \right)}}{{2\left( {1 + \cos \alpha } \right)}} = \dfrac{{{a^6}\left( {1 - \cos \alpha } \right)\left( {1 + 2\cos \alpha } \right)}}{{18}}\end{array}$

Đặt $t = \cos \alpha \left( {t \in \left[ { - 1;1} \right]} \right)$ và xét hàm $f\left( t \right) = \left( {1 - t} \right)\left( {1 + 2t} \right) =  - 2{t^2} + t + 1$ trên $\left[ { - 1;1} \right]$ có:

Hàm bậc hai $f\left( t \right) =  - 2{t^2} + t + 1$ có đồ thị là parabol với bề lõm hướng xuống dưới.

Do đó nó đạt GTLN tại $t = \dfrac{1}{4}$ và $\mathop {\max }\limits_{\left[ { - 1;1} \right]} f\left( t \right) = f\left( {\dfrac{1}{4}} \right) = \dfrac{9}{8}$.

Khi đó $V_{\max }^2 = \dfrac{{{a^6}}}{{18}}.\dfrac{9}{8} = \dfrac{{{a^6}}}{{16}} \Rightarrow V = \dfrac{{{a^3}}}{4}$