Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $B$, $AB = a.$ Cạnh bên $SA = a$ và vuông góc với đáy. Mặt phẳng qua $A$ vuông góc với $SC$ cắt hình chóp theo một thiết diện. Tính diện tích thiết diện đó.
Trả lời bởi giáo viên
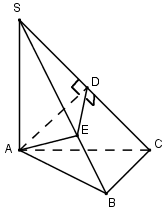
Trong $(SAC)$ qua $A$ kẻ \(AD \bot SC\,\,\left( {D \in SC} \right)\), trong $(SBC)$ qua $D$ kẻ \(DE \bot SC\,\,\left( {E \in SB} \right)\). Khi đó mặt phẳng qua $A$ vuông góc với $SC $ cắt hình chóp theo một thiết diện là tam giác $ADE.$
Tam giác $ABC$ vuông cân tại $B$ nên \(AC = AB\sqrt 2 = a\sqrt 2 \)
Xét tam giác vuông $SAC:$ \(\dfrac{{SD}}{{SC}} = \dfrac{{S{A^2}}}{{S{C^2}}} = \dfrac{{S{A^2}}}{{S{A^2} + A{C^2}}} = \dfrac{1}{3}\)
Xét tam giác vuông $SAB:$ \(\dfrac{{SE}}{{SB}} = \dfrac{{S{A^2}}}{{S{B^2}}} = \dfrac{{S{A^2}}}{{S{A^2} + A{B^2}}} = \dfrac{1}{2}\)
$ \Rightarrow \dfrac{{{V_{S.ADE}}}}{{{V_{S.ACB}}}} = \dfrac{{SD}}{{SC}}.\dfrac{{SE}}{{SB}} = \dfrac{1}{6} \Rightarrow {V_{S.ADE}} = \dfrac{1}{6}{V_{S.ACB}} = \dfrac{1}{6}.\dfrac{1}{3}SA.\dfrac{1}{2}BA.BC = \dfrac{{{a^3}}}{{36}}$
Mà \(SC \bot \left( {ADE} \right) \Rightarrow {V_{S.ADE}} = \dfrac{1}{3}SD.{S_{ADE}} \Rightarrow {S_{ADE}} = \dfrac{{3{V_{S.ADE}}}}{{SD}} = \dfrac{{3{V_{S.ADE}}}}{{\dfrac{1}{3}SC}} = \dfrac{{9{V_{S.ADE}}}}{{\sqrt {S{A^2} + A{C^2}} }} = \dfrac{{9.\dfrac{{{a^3}}}{{36}}}}{{\sqrt {{a^2} + 2{a^2}} }} = \dfrac{{{a^2}\sqrt 3 }}{{12}}\)
Hướng dẫn giải:
Giả sử mặt phẳng qua $A$ vuông góc với $SC$ cắt hình chóp theo một thiết diện là tam giác $ADE.$
$\begin{array}{l}\dfrac{{{V_{S.ADE}}}}{{{V_{S.ACB}}}} = \dfrac{{SD}}{{SC}}.\dfrac{{SE}}{{SB}} \Rightarrow {V_{S.ADE}}\\{V_{S.ADE}} = \dfrac{1}{3}SD.{S_{ADE}} \Rightarrow {S_{ADE}}\end{array}$

