Cho khối chóp $S.ABC$ có điểm $M$ và $N$ lần lượt nằm trên các cạnh $SA$ và $SB$ sao cho $\dfrac{{SM}}{{SA}} = \dfrac{1}{3},\,\dfrac{{SN}}{{SB}} = \dfrac{2}{3}$. Mặt phẳng $\left( \alpha  \right)$ qua hai điểm $M, N$ và song song $SC$ chia khối chóp thành $2$ khối đa diện. Tính tỉ số thể tích của khối đa diện có thể tích lớn hơn so với thể tích khối chóp $S.ABC.$

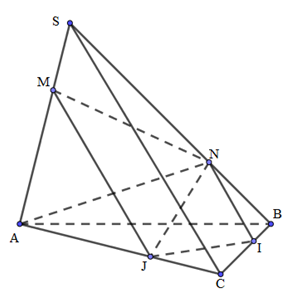
Trong mặt phẳng $\left( {SBC} \right)$ : kẻ $NI//SC,I \in BC$ .

Trong mặt phẳng $\left( {SAC} \right)$ : kẻ $MJ//SC,J \in AC$ .

$\Rightarrow$ Thiết diện của hình chóp cắt bởi $\left( \alpha  \right)$  là $MNIJ$.

Ta tính tỉ số thế tích của khối đa diện $MNBIJA$ với khối chóp $S.ABC$:

Ta có:

$\begin{array}{l}\dfrac{{{V_{N.MAJ}}}}{{{V_{S.ABC}}}} = \dfrac{{\dfrac{1}{3}.d(N,\,(SAC)).\,{S_{AMJ}}}}{{\dfrac{1}{3}.d(B,(SAC)).{S_{SAC}}}} = \dfrac{{d(N,\,(SAC))}}{{d(B,\,(SAC))}}.\dfrac{{{S_{AMJ}}}}{{{S_{SAC}}}}\\ = \dfrac{{SN}}{{BS}}.\dfrac{{AM}}{{SA}}.\dfrac{{AJ}}{{AC}} = \dfrac{2}{3}.\dfrac{2}{3}.\dfrac{2}{3} = \dfrac{8}{{27}} \Rightarrow {V_{N.MAJ}} = \dfrac{8}{{27}}{V_{S.ABC}}\,\,(1)\end{array}$

$\dfrac{{{V_{N.ABIJ}}}}{{{V_{S.ABC}}}} = \dfrac{{\dfrac{1}{3}.d(N,(ABC)).{S_{ABIJ}}}}{{\dfrac{1}{3}.d(S,(ABC)).{S_{ABC}}}} = \dfrac{{d(N,(ABC))}}{{d(S,(ABC))}}.\dfrac{{{S_{ABIJ}}}}{{{S_{ABC}}}} = \dfrac{{NB}}{{SB}}.\dfrac{{{S_{ABIJ}}}}{{{S_{ABC}}}} = \dfrac{1}{3}.\dfrac{7}{9} = \dfrac{7}{{27}}$    (vì $\dfrac{{{S_{CIJ}}}}{{{S_{ABC}}}} = \dfrac{{IC}}{{BC}}.\dfrac{{JC}}{{AC}} = \dfrac{2}{3}.\dfrac{1}{3} = \dfrac{2}{9}$ ).

 $\Rightarrow {V_{N.ABIJ}} = \dfrac{7}{{27}}{V_{S.ABC}}\,\,(2)$

Từ (1), (2) suy ra ${V_{N.AMJ}} + {V_{N.ABIJ}} = \left( {\dfrac{8}{{27}} + \dfrac{7}{{27}}} \right){V_{S.ABC}} \Leftrightarrow {V_{MNBIJA}} = \dfrac{5}{9}{V_{S.ABC}} \Rightarrow \dfrac{{{V_{MNBIJA}}}}{{{V_{S.ABC}}}} = \dfrac{5}{9}$