Người ta cần chế tạo các món quà lưu niệm bằng đồng có dạng khối chóp tứ giác đều, được mạ vàng bốn mặt bên và có thể tích bằng 49 cm³. Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu cm²? (Kết quả làm tròn đến hàng đơn vị)

Điền số nguyên hoặc phân số dạng a/b

Đáp án:

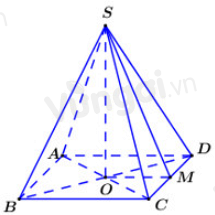
Gọi khối chóp tứ giác đều thỏa mãn yêu cầu bài toán là \(S.ABCD\).

Gọi \(O = AC \cap BD\).

Đặt \(AB = x\,\,\left( {x > 0} \right)\).

\( \Rightarrow {S_{ABCD}} = {x^2}\).

Khi đó \({V_{S.ABCD}} = \dfrac{1}{3}.SO.{S_{ABCD}}\)

\( \Leftrightarrow \dfrac{1}{3}SO.{x^2} = 49\)

\( \Leftrightarrow SO = \dfrac{{147}}{{{x^2}}}\).

Gọi \(M\) là trung điểm của \(CD\). Suy ra \(OM\) là đường trung bình của tam giác \(BCD\).

Khi đó \(OM//BC\) và \(OM = \dfrac{1}{2}BC = \dfrac{x}{2}\).

Ta có \(SM = \sqrt {S{O^2} + O{M^2}}  = \sqrt {{{\left( {\dfrac{{147}}{{{x^2}}}} \right)}^2} + {{\left( {\dfrac{x}{2}} \right)}^2}}  = \sqrt {\dfrac{{{{147}^2}}}{{{x^4}}} + \dfrac{{{x^2}}}{4}} \)

Ta có \(\left\{ \begin{array}{l}CD \bot OM\,\,\left( {OM//BC} \right)\\CD \bot SO\,\,\left( {SO \bot \left( {ABCD} \right)} \right)\\Trong\,\,\left( {SOM} \right):SO \cap OM = O\end{array} \right.\)

\( \Rightarrow CD \bot \left( {SOM} \right)\).

Mà \(SM \subset \left( {SOM} \right)\).

\( \Rightarrow CD \bot SM\).

Ta có \({S_{SCD}} = \dfrac{1}{2}SM.CD = \dfrac{1}{2}.\sqrt {\dfrac{{{{147}^2}}}{{{x^4}}} + \dfrac{{{x^2}}}{4}} .x = \dfrac{1}{2}.\sqrt {\dfrac{{{{147}^2}}}{{{x^2}}} + \dfrac{{{x^4}}}{4}} \)

Để diện tích mạ vàng nhỏ nhất thì \({S_{SCD}}\) nhỏ nhất.

\( \Leftrightarrow \sqrt {\dfrac{{{{147}^2}}}{{{x^2}}} + \dfrac{{{x^4}}}{4}} \) nhỏ nhất.

Ta có \(\dfrac{{{{147}^2}}}{{{x^2}}} + \dfrac{{{x^4}}}{4} = \dfrac{{10804}}{{{x^2}}} + \dfrac{{10805}}{{{x^2}}} + \dfrac{{{x^4}}}{4} \ge 3.\sqrt[3]{{\dfrac{{10804}}{{{x^2}}}.\dfrac{{10805}}{{{x^2}}}.\dfrac{{{x^4}}}{4}}}\)

\( = 3.\sqrt[3]{{\dfrac{{10804}}{{{x^2}}}.\dfrac{{10805}}{{{x^2}}}.\dfrac{{{x^4}}}{4}}} = 3\sqrt[3]{{29184305}}\) (theo bất đẳng thức Cauchy).

Vậy diện tích mạ vàng nhỏ nhất bằng \(4.{S_{SCD\,\min }} = 4.\dfrac{1}{2}\sqrt {3.\sqrt[3]{{29184305}}}  \approx 60,783\) (cm²).