Khối đa diện nào có số đỉnh nhiều nhất?
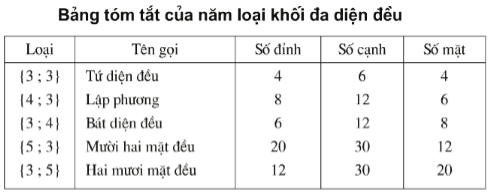
Khối đa diện đều có nhiều đỉnh nhất là khối nhị thập diện đều (12 mặt đều) với 20 đỉnh.
Khối bát diện đều là khối đa diện đều loại
Khối bát diện đều là khối đa diện loại \(\left\{ {3;4} \right\}\).
Cho phép vị tự tâm \(O\) tỉ số \(k \ne 0\) biến điểm \(M\) thành điểm \(M'\). Chọn mệnh đề đúng:
Phép vị tự tâm \(O\) tỉ số \(k\) biến điểm \(M\) thành \(M'\) thì $OM' = \left| k \right|OM$
Cho phép vị tự tâm \(O\) tỉ số \(k < 0\) lần lượt biến điểm \(M,N\) thành \(M',N'\), chọn mệnh đề đúng:
Phép vị tự tâm \(O\) biến \(M,N\) thành \(M',N'\) nên \(\overrightarrow {M'N'} = k\overrightarrow {MN} \) và \(M'N' = \left| k \right|MN\)
Do \(k < 0\) nên \(M'N' = - kMN\).
Cho điểm \(O\) cố định trong không gian. Chọn mệnh đề đúng:
Có \(2\) phép vị tự tâm \(O\) là phép dời hình, đó là các phép vị tự tâm \(O\) tỉ số vị tự bằng \( \pm 1\).
Tính tổng diện tích tất cả các mặt của khối đa diện đều loại \(\left\{ {3;5} \right\}\) có các cạnh bằng \(1\).
Khối đa diện đều loại \(\left\{ {3;5} \right\}\) là khối 20 mặt đều.
Khối 20 mặt đều thì 1 mặt là tam giác đều cạnh bằng 1 có diện tích một mặt bằng: \(S = \dfrac{{\sqrt 3 }}{4}\)
Vậy diện tích tất cả các mặt của khối đa diện là \(S' = 20.\dfrac{{\sqrt 3 }}{4} = 5\sqrt 3 \).
Hình bát diện đều có số cạnh là:
Hình bát diện đều có số cạnh là 12.
Phép đối xứng tâm \(O\) cố định là phép vị tự tâm \(O\) tỉ số:
Phép đối xứng tâm \(O\) cố định là phép vị tự tâm \(O\) tỉ số \(k = - 1\)
Có bao nhiêu loại khối đa diện mà mỗi mặt của nó là một tam giác đều.
Các khối đa diện mà mỗi mặt của nó là một tam giác đều là:
- Khối \(\left\{ {3;3} \right\}\): Tứ diện đều.
- Khối \(\left\{ {3;4} \right\}\): Bát diện đều.
- Khối \(\left\{ {3;5} \right\}\): Khối 20 mặt đều.
Vậy có 3 khối đa diện mà mỗi mặt của nó là một tam giác đều.
Chọn khẳng định đúng:
Hai tứ diện đều thì đồng dạng nên A đúng.
Diện tích toàn phần của hình bát diện đều cạnh bằng \(2a\) là
Tam giác đều có cạnh bằng 2a có diện tích \(S = \dfrac{{\sqrt 3 }}{4}{\left( {2a} \right)^2} = {a^2}\sqrt 3 .\)
Vậy diện tích toàn phần của bát diện đều là \(8{a^2}\sqrt 3 .\)
Khối đa diện đều loại \(\left\{ {n;p} \right\}\) thì \(p\) là:
- Khối đa diện đều loại \(\left\{ {n;p} \right\}\):
+ \(n\) là số cạnh của mỗi mặt.
+ \(p\) là số cạnh cùng đi qua một đỉnh.
Tổng số cạnh và số đỉnh của hình bát diện đều bằng bao nhiêu ?
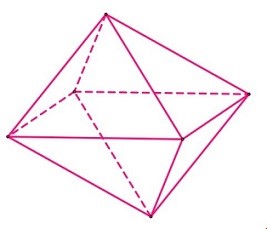
Hình bát diện đều có 12 cạnh và 6 đỉnh.
Vậy tổng số cạnh và đỉnh là 12 + 6 = 18
Cho hình bát diện đều cạnh \(2\). Gọi \(S\) là tổng diện tích tất cả các mặt bên của hình bát diện đó. Khi đó \(S\) bằng:
Bát diện đều là hình có 8 mặt là tam giác đều, các mặt là tam giác đều cạnh \(2\).
Diện tích một mặt là \(S = \dfrac{{{2^2}\sqrt 3 }}{4} = \sqrt 3 \).
Vậy tổng diện tích các mặt của hình bát diện đó là \(8\sqrt 3 \).
Khối đa diện lồi có \(8\) đỉnh và \(6\) mặt thì có số cạnh là:
Ta có: \(D = 8,M = 6\) thì \(D - C + M = 2 \Leftrightarrow 8 - C + 6 = 2 \Leftrightarrow C = 12\)
Vậy số cạnh là \(12\).
Đa diện đều loại \(\left\{ {5;3} \right\}\) có tên gọi nào dưới đây?
Đa diện đều loại \(\left\{ {5;3} \right\}\) có tên gọi là Mười hai mặt đều.
Trong các khẳng định sau, khẳng định nào đúng?
Khối đa diện đều loại \(\left\{ {p;q} \right\}\) là khối đa diện lồi thỏa mãn mỗi mặt của nó là đa giác đều \(p\) cạnh và mỗi đỉnh của nó là đỉnh chung của đúng \(q\) mặt.
Do đó đáp án đúng là B.
Số đỉnh của khối bát diện đều là:
Hình bát diện đều có 6 đỉnh.
Cho phép vị tự tâm \(O\) tỉ số \(k \ne 0\) biến điểm \(M\) thành điểm \(M'\). Chọn mệnh đề đúng:
Phép vị tự tâm \(O\) tỉ số \(k\) biến điểm \(M\) thành \(M'\) nếu \(\overrightarrow {OM'} = k\overrightarrow {OM} \).
Cho phép vị tự tâm \(O\) tỉ số \(k < 0\) lần lượt biến điểm \(M,N\) thành \(M',N'\), chọn mệnh đề sai:
Các đáp án A, B, C đều đúng.
Đáp án D sai vì \(\overrightarrow {M'N'} = k.\overrightarrow {MN} \Rightarrow M'N' = \left| k \right|MN \Rightarrow M'N' = - k.MN\left( {k < 0} \right)\)

