Dạng lượng giác của số phức

- Số phức \(z = r\left( {\cos \varphi  + i\sin \varphi } \right)\) là dạng lượng giác của \(z\), ở đó:

+ \(r\) là mô đun của số phức.

+ \(\varphi \) là acgumen của số phức.

- Số phức \(z = r\left( {\cos \varphi  + i\sin \varphi } \right)\) là dạng lượng giác của \(z\), ở đó:

+ \(r\) là mô đun của số phức.

+ \(\varphi \) là acgumen của số phức.

- Nếu \(\varphi \) là một acgumen của \(z\) thì \(\varphi  + k2\pi \) cũng là một acgumen của \(z\) với mỗi \(k \in Z\).

Vì \(z = r\left( {\cos \dfrac{\pi }{4} + i\sin \dfrac{\pi }{4}} \right)\) nên \(\varphi  = \dfrac{\pi }{4}\) là 1 acgumen của \(z\).

Do đó \(\dfrac{\pi }{4} + k2\pi \) cũng là 1 acgumen của \(z\).

Ta có: \( - \dfrac{\pi }{4} - \dfrac{\pi }{4} =  - \dfrac{\pi }{2} \ne k2\pi ,\forall k \in Z\) nên A sai.

\( - \dfrac{{5\pi }}{4} - \dfrac{\pi }{4} =  - \dfrac{{3\pi }}{2} \ne k2\pi ,\forall k \in Z\) nên B sai.

\(\dfrac{{5\pi }}{4} - \dfrac{\pi }{4} = \pi  \ne k2\pi ,\forall k \in Z\) nên C sai.

\(\dfrac{{9\pi }}{4} - \dfrac{\pi }{4} = 2\pi \) nên D đúng.

Số phức \(z\) có mô đun \(r = 3\) và acgumen \(\varphi  =  - \dfrac{\pi }{3}\) thì có dạng lượng giác là \(z = 3\left( {\cos \left( { - \dfrac{\pi }{3}} \right) + i\sin \left( { - \dfrac{\pi }{3}} \right)} \right)\)

Ta có:

\(z =  - r\left( {\cos \varphi  + i\sin \varphi } \right) = r\left( { - \cos \varphi  - i\sin \varphi } \right) = z = r'\left( {\cos \varphi ' + i\sin \varphi '} \right)\)

Suy ra \(\left\{ \begin{array}{l}\cos \varphi ' =  - \cos \varphi \\\sin \varphi ' =  - \sin \varphi \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\cos \varphi ' = \cos \left( {\varphi  + \pi } \right)\\\sin \varphi ' = \sin \left( {\varphi  + \pi } \right)\end{array} \right. \Rightarrow \varphi ' = \varphi  + \pi \)

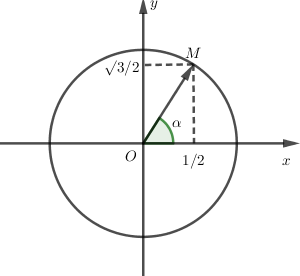
Quan sát hình vẽ ta thấy \(\left\{ \begin{array}{l}\sin \varphi  = \dfrac{{\sqrt 3 }}{2}\\\cos \varphi  = \dfrac{1}{2}\end{array} \right. \Rightarrow \varphi  = \dfrac{\pi }{3}\)

Vì \(r\) là mô đun của số phức nên \(r = \sqrt {{a^2} + {b^2}} \)

Ta có: \(z = 4\left( {\cos \left( { - \dfrac{\pi }{2}} \right) + i\sin \left( { - \dfrac{\pi }{2}} \right)} \right) = 4\left( {0 + i.\left( { - 1} \right)} \right) =  - 4i\)

Ta có: \(z = i - 1 =  - 1 + i \Rightarrow a =  - 1;b = 1\)

- Tính \(r = \sqrt {{{\left( { - 1} \right)}^2} + {1^2}}  = \sqrt 2 \).

- Tính \(\varphi \) thỏa mãn $\left\{ \begin{array}{l}\cos \varphi  = \dfrac{a}{r} =  - \dfrac{1}{{\sqrt 2 }}\\\sin \varphi  = \dfrac{b}{r} = \dfrac{1}{{\sqrt 2 }}\end{array} \right. \Rightarrow \varphi  = \dfrac{{3\pi }}{4}$

Vậy \(z = \sqrt 2 \left( {\cos \dfrac{{3\pi }}{4} + i\sin \dfrac{{3\pi }}{4}} \right)\).

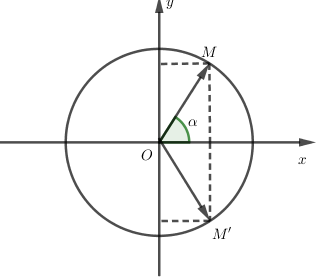
Số phức \(z\) có điểm biểu diễn là \(M\) thì \(\overline z \) có điểm biểu diễn là \(M'\) đối xứng với \(M\) qua \(Ox\). Do đó \( - \varphi \) là một argument của \(\overline z \).

Số phức $z=a+bi$ được viết dưới dạng lượng giác là \(z = r.\left( {\cos \varphi  + i\sin \varphi } \right)\)

Với \(r = \left| z \right|\) và \(\varphi \) là argument của $z$.

Khi đó

\(\begin{array}{l}\overline z  = r.\left( {\cos \varphi  - i.\sin \varphi } \right)\\ = r.\left[ {\cos \left( { - \varphi } \right) + i.\sin \left( { - \varphi } \right)} \right]\end{array}\)

Ta có: \(\dfrac{1}{z} = \dfrac{{\overline z }}{{z.\overline z }} = \dfrac{1}{{{{\left| z \right|}^2}}}.\overline z \).

Vì \(\dfrac{1}{{{{\left| z \right|}^2}}}\) là số thực nên acgumen của \(\dfrac{1}{z}\) cũng là acgumen của \(\overline z \).

Mà \( - \varphi \) là một acgumen của \(\overline z \) nên \( - \varphi \) cũng là một acgumen của \(\dfrac{1}{z}\).

Ta có: \(z =  - 1 =  - 1 + 0i \Rightarrow r = \sqrt {{{\left( { - 1} \right)}^2} + {0^2}}  = 1\)

Acgumen \(\varphi \) thỏa mãn \(\left\{ \begin{array}{l}\cos \varphi  =  - 1\\\sin \varphi  = 0\end{array} \right. \Rightarrow \varphi  = \pi  + k2\pi \)

Quan sát các đáp án ta thấy chỉ có đáp án A thỏa mãn.

Cho hai số phức \({z_1} = {r_1}\left( {\cos {\varphi _1} + i\sin {\varphi _1}} \right),{z_2} = {r_2}\left( {\cos {\varphi _2} + i\sin {\varphi _2}} \right)\).

Khi đó \({z_1}{z_2} = {r_1}{r_2}\left[ {\cos \left( {{\varphi _1} + {\varphi _2}} \right) + i\sin \left( {{\varphi _1} + {\varphi _2}} \right)} \right]\)

Ta có:

\({z_1} = 3\left( {\cos \dfrac{\pi }{3} + i\sin \dfrac{\pi }{3}} \right),{z_2} = 2\left( {\cos \dfrac{\pi }{4} + i\sin \dfrac{\pi }{4}} \right) \)

$\Rightarrow \dfrac{{{z_1}}}{{{z_2}}} = \dfrac{3}{2}\left[ {\cos \left( {\dfrac{\pi }{3} - \dfrac{\pi }{4}} \right) + i\sin \left( {\dfrac{\pi }{3} - \dfrac{\pi }{4}} \right)} \right] = \dfrac{3}{2}\left( {\cos \dfrac{\pi }{{12}} + i\sin \dfrac{\pi }{{12}}} \right)$

Cho số phức \(z = r\left( {\cos \varphi  + i\sin \varphi } \right)\). Khi đó \({z^n} = {\left[ {r\left( {\cos \varphi  + i\sin \varphi } \right)} \right]^n} = {r^n}\left( {\cos n\varphi  + i\sin n\varphi } \right)\)

Phương trình ${z^2} + z + 1 = 0$ có $\Delta  = 1-4 = -3$  nên có $2$  nghiệm ${z_1} = \dfrac{{ - 1 + i\sqrt 3 }}{2};{z_2} = \dfrac{{ - 1 - i\sqrt 3 }}{2}$

$\begin{array}{l}z_1^{2017} + z_2^{2017} = {\left( { - \dfrac{1}{2} + i\dfrac{{\sqrt 3 }}{2}} \right)^{2017}} + {\left( { - \dfrac{1}{2} - i\dfrac{{\sqrt 3 }}{2}} \right)^{2017}}\\ = {\left( {\cos \dfrac{{2\pi }}{3} + i\sin \dfrac{{2\pi }}{3}} \right)^{2017}} + {\left[ {\cos \left( { - \dfrac{{2\pi }}{3}} \right) + i\sin \left( { - \dfrac{{2\pi }}{3}} \right)} \right]^{2017}}\\ = \cos \left( {\dfrac{{2017.2\pi }}{3}} \right) + i\sin \left( {\dfrac{{2017.2\pi }}{3}} \right) + \cos \left( { - \dfrac{{2017.2\pi }}{3}} \right) + i\sin \left( { - \dfrac{{2017.2\pi }}{3}} \right)\\ = 2\cos \dfrac{{4034\pi }}{3} = 2\cos \dfrac{{2\pi }}{3} =  - 1\end{array}$

Ta thấy \(z + \dfrac{1}{z} = 1 \Leftrightarrow {z^2} - z + 1 = 0 \Rightarrow z = \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\) 

Ta chỉ cần lấy 1 nghiệm do \({z_1}.{z_2} = 1\) và vai trò của \({z_1}\) và \({z_2}\) trong biểu thức \({z^{2017}} + \frac{1}{{{z^{2017}}}}\) là như nhau.

Lại có: \(z = \cos \dfrac{\pi }{3} + i\sin \dfrac{\pi }{3} \Rightarrow {z^{2017}} = \cos \dfrac{{2017.\pi }}{3} + i\sin \dfrac{{2017.\pi }}{3} = \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\)

Suy ra \(\dfrac{1}{{{z^{2017}}}} = \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2}i\)

$\begin{array}{l}{\left( {1 + i} \right)^{19}} = \sum\limits_{k = 0}^{19} {C_9^k{i^k}}  = C_{19}^0{i^0} + C_{19}^1{i^1} + C_{19}^2{i^2} + C_{19}^3{i^3} + ... + C_{19}^{18}{i^{18}} + C_{19}^{19}{i^{19}}\\ = C_{19}^0 + C_{19}^1i - C_{19}^2 - C_{19}^3i + ... - C_{19}^{18} - C_{19}^{19}i\\ = \left( {C_{19}^0 - C_{19}^2 + C_{19}^4 - ... + C_{19}^{16} - C_{19}^{18}} \right) + i\left( {C_{19}^1 - C_{19}^3 + C_{19}^5 - ... + C_{19}^{17} - C_{19}^{19}} \right)\end{array}$

Nên phần thực của ${\left( {1 + i} \right)^{19}}$ là $C_{19}^0 - C_{19}^2 + C_{19}^4 - ... + C_{19}^{16} - C_{19}^{18}$

Lại có:

\(\begin{array}{l}1 + i = \sqrt 2 \left( {\cos \dfrac{\pi }{4} + i\sin \dfrac{\pi }{4}} \right)\\ \Rightarrow {\left( {1 + i} \right)^{19}} = {\sqrt 2 ^{19}}\left( {\cos \dfrac{{19\pi }}{4} + i\sin \dfrac{{19\pi }}{4}} \right) = {\sqrt 2 ^{19}}\left( { - \dfrac{{\sqrt 2 }}{2} + i\dfrac{{\sqrt 2 }}{2}} \right) \\ =  - \dfrac{{{{\sqrt 2 }^{20}}}}{2} + \dfrac{{{{\sqrt 2 }^{20}}}}{2}i =  - 512 + 512i\end{array}\)

Vậy phần thực của \({\left( {1 + i} \right)^{19}}\) là \( - 512\).

Do đó $C_{19}^0 - C_{19}^2 + C_{19}^4 - ... + C_{19}^{16} - C_{19}^{18} =  - 512$

Ta có: \(z =  - 2 + 2\sqrt 3 i = 4\left( { - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i} \right) = 4\left( {\cos \dfrac{{2\pi }}{3} + i\sin \dfrac{{2\pi }}{3}} \right)\)

$ \Rightarrow {z^n} = {4^n}\left( {\cos \dfrac{{2n\pi }}{3} + i\sin \dfrac{{2n\pi }}{3}} \right)$

\({z^n}\) là số thực \( \Leftrightarrow \sin \dfrac{{2n\pi }}{3} = 0 \Leftrightarrow \dfrac{{2n\pi }}{3} = k\pi  \Leftrightarrow n = \dfrac{{3k}}{2}\)

Do \(n\) nguyên dương nên \(\dfrac{{3k}}{2} \in {N^*} \Leftrightarrow k = 2m,m \in {N^*} \Rightarrow n = \dfrac{{3k}}{2} = \dfrac{{3.2m}}{2} = 3m,m \in {N^*}\)

Vậy \(n = 3m,m \in {N^*}\).