Tổng hợp câu hay và khó chương 4 phần 2

Giả sử $z = x + yi{\rm{ }}\left( {x,y \in R} \right) \Rightarrow {\left( {x + yi} \right)^2} = \left( {{x^2} + {y^2}} \right) + \left( {x - yi} \right)$

$\begin{array}{l} \Leftrightarrow {x^2} - {y^2} + 2xyi = {x^2} + {y^2} + x - yi \Leftrightarrow \left\{ \begin{array}{l}2xy =  - y\\{x^2} - {y^2} = {x^2} + {y^2} + x\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}y = 0\\x =  - \dfrac{1}{2}\end{array} \right.\\2{y^2} + x = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}y = 0\\x = 0\end{array} \right.\\\left\{ \begin{array}{l}x =  - \dfrac{1}{2}\\2{y^2} - \dfrac{1}{2} = 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = y = 0\\\left\{ \begin{array}{l}x =  - \dfrac{1}{2}\\y =  \pm \dfrac{1}{2}\end{array} \right.\end{array} \right.\end{array}$

Do đó có 3 số phức $z$ thỏa mãn bài toán.

Ta có

$\begin{array}{l}\left| {{z^2} + 1} \right| = 2\left| z \right| \Leftrightarrow {\left| {{z^2} + 1} \right|^2} = 4{\left| z \right|^2} \Leftrightarrow \left( {{z^2} + 1} \right)\left( {\overline {{z^2} + 1} } \right) = 4z\overline z \\ \Leftrightarrow \left( {{z^2} + 1} \right)\left( {{{\overline z }^2} + 1} \right) = 4z\overline z  \Leftrightarrow {\left( {z\overline z } \right)^2} + {z^2} + {\overline z ^2} + 1 - 4z\overline z  = 0\\ \Leftrightarrow {\left( {z + \overline z } \right)^2} + {\left( {z\overline z } \right)^2} - 6z\overline z  + 1 = 0\\ \Leftrightarrow {\left( {z + \overline z } \right)^2} + {\left| z \right|^4} - 6{\left| z \right|^2} + 1 = 0\\ \Leftrightarrow {\left| z \right|^4} - 6{\left| z \right|^2} + 1 =  - {\left( {z + \overline z } \right)^2} \le 0\\ \Leftrightarrow 3 - 2\sqrt 2  \le {\left| z \right|^2} \le 3 + 2\sqrt 2 \\ \Leftrightarrow \sqrt 2  - 1 \le \left| z \right| \le \sqrt 2  + 1 \Rightarrow \left\{ \begin{array}{l}\left| {{z_1}} \right| = \sqrt 2  - 1\\\left| {{z_2}} \right| = \sqrt 2  + 1\end{array} \right.\end{array}$

Dấu = xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}\left| {{z_1}} \right| = \sqrt 2  - 1\\\left| {{z_2}} \right| = \sqrt 2  + 1\\z + \overline z  = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}{z_1} = \left( {\sqrt 2  - 1} \right)i\\{z_1} = \left( {1 - \sqrt 2 } \right)i\end{array} \right.\\\left[ \begin{array}{l}{z_2} = \left( {\sqrt 2  + 1} \right)i\\{z_2} = \left( { - \sqrt 2  - 1} \right)i\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left| w \right| = \left| {{z_1} + {z_2}} \right| = 2\sqrt 2 \\\left| w \right| = \left| {{z_1} + {z_2}} \right| = 2\end{array} \right.\) 

Theo bài ra, ta có \(\left\{ \begin{array}{l}\left| {z - 1 + 2i} \right| = 5\\z.\bar z = 10\end{array} \right. \Leftrightarrow \,\,\left\{ \begin{array}{l}\left| {\left( {a - 1} \right) + \left( {b + 2} \right)i} \right| = 5\\\left( {a + bi} \right)\left( {a - bi} \right) = 10\end{array} \right. \Leftrightarrow \,\,\left\{ \begin{array}{l}{\left( {a - 1} \right)^2} + {\left( {b + 2} \right)^2} = 25\\{a^2} + {b^2} = 10\end{array} \right.\)

$\begin{array}{l} \Leftrightarrow \,\,\left\{ \begin{array}{l}{a^2} + {b^2} = 10\\{a^2} + {b^2} - 2a + 4b = 20\end{array} \right. \Leftrightarrow \,\,\left\{ \begin{array}{l}2a - 4b =  - \,10\\{a^2} + {b^2} = 10\end{array} \right. \Leftrightarrow \,\,\left\{ \begin{array}{l}a = 2b - 5\\{a^2} + {b^2} = 10\end{array} \right.\\ \Rightarrow \,\,\left\{ \begin{array}{l}a = 2b - 5\\{\left( {2b - 5} \right)^2} + {b^2} = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2b - 5\\\left[ \begin{array}{l}b = 1\\b = 3\end{array} \right.\end{array} \right. \Rightarrow \left[ \begin{array}{l}\,\,\left\{ \begin{array}{l}a =  - \,3\\b = 1\end{array} \right.\left( {ktm} \right)\\\left\{ \begin{array}{l}a = 1\\b = 3\end{array} \right.\;\;\left( {tm} \right)\end{array} \right..\\ \Rightarrow P = a - b = 1 - 3 =  - 2.\end{array}$

Theo bài ra, ta có

\(\left| {z - 1 - i} \right| = 1 \Rightarrow \) Tập hợp biểu diễn số phức \(z\) là đường tròn \(\left( {{C_1}} \right)\) có tâm \({I_1}\left( {1;1} \right)\) và bán kính \({R_1} = 1\).

\(\left| {\bar w - 2 - 3i} \right| = 2 \Leftrightarrow \left| {w - 2 + 3i} \right| = 2 \Rightarrow \) Tập hợp biểu diễn số phức \(w\) là đường tròn \(\left( {{C_2}} \right)\) có tâm \({I_2}\left( {2; - \,3} \right)\) và bán kính \({R_2} = 2.\)

Do \({I_1}{I_2} > {R_1} + {R_2}\) nên hai đường tròn không cắt nhau.

Khi đó \(\left| {z - w} \right| = MN \Rightarrow {\left| {z - w} \right|_{\min }} = M{N_{\min }} = {I_1}{I_2} - \left( {{R_1} + {R_2}} \right) = \sqrt {17}  - 3\). 

\(\begin{array}{l}\,\,\,\,\,\left( {3 + i} \right)\left| z \right| = \dfrac{{ - 2 + 14i}}{z} + 1 - 3i\\ \Leftrightarrow \left( {3 + i} \right)\left| z \right| - 1 + 3i = \dfrac{{ - 2 + 14i}}{z}\\ \Leftrightarrow \left( {3\left| z \right| - 1} \right) + \left( {\left| z \right| + 3} \right)i = \dfrac{{ - 2 + 14i}}{z}\end{array}\)

Lấy mođun hai vế ta có : \(\sqrt {9{{\left| z \right|}^2} - 6\left| z \right| + 1 + {{\left| z \right|}^2} + 6\left| z \right| + 9}  = \dfrac{{10\sqrt 2 }}{{\left| z \right|}}\)

$ \Leftrightarrow 10{\left| z \right|^2} + 10 = \dfrac{{200}}{{{{\left| z \right|}^2}}} \Leftrightarrow {\left| z \right|^4} + {\left| z \right|^2} - 20 = 0 \Leftrightarrow {\left| z \right|^2} = 4 \Rightarrow \left| z \right| = 2 \in \left( {\dfrac{7}{4};\dfrac{{11}}{5}} \right)$

Đặt $z = x + yi\,\,\,\,\left( {x,y \in \mathbb{R}} \right)$ suy ra tập hợp các điểm $M\left( z \right) = \left( {x;y} \right)$ là đường tròn $\left( C \right)$ có tâm $I\left( {3;4} \right)$ và bán kính $R = \sqrt 5 .$ Ta có $P = {\left| {z + 2} \right|^2} - {\left| {z - i} \right|^2} = {\left| {x + 2 + yi} \right|^2} - {\left| {x + \left( {y - 1} \right)i} \right|^2} = {\left( {x + 2} \right)^2} + {y^2} - {x^2} - {\left( {y - 1} \right)^2}$

\( = {x^2} + {y^2} + 4x + 4 - {x^2} - {y^2} + 2y - 1 \) \(= 4x + 2y + 3\)

\( \Rightarrow \left( \Delta \right):4x + 2y + 3 - P = 0.\)

Ta cần tìm $P$ sao cho đường thẳng $\left( \Delta  \right)$ và đường tròn $\left( C \right)$ có điểm chung $ \Leftrightarrow $$d\left( {I;\left( \Delta  \right)} \right) \le R.$

$ \Leftrightarrow \dfrac{{\left| {4.3 + 2.4 + 3 - P} \right|}}{{\sqrt {{4^2} + {2^2}} }} \le \sqrt 5  \Leftrightarrow \left| {23 - P} \right| \le 10 \Leftrightarrow  - \,10 \le 23 - P \le 10 \Leftrightarrow 13 \le P \le 33.$

Do đó, $\left\{ \begin{array}{l}\max P = 33\\\min P = 13\end{array} \right. \Rightarrow \,\,w = M + mi = 33 + 13i.$ Vậy $\left| w \right| = \sqrt {1258} .$

Đặt $z = x + yi\,\,\,\,\left( {x,\,\,y \in \mathbb{R}} \right),$ khi đó ${\left| {z - {z_1}} \right|^2} + {\left| {z - {z_2}} \right|^2} = 16 \Leftrightarrow {\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 16$

$ \Leftrightarrow 2{x^2} + 4 + 2{y^2} - 4y + 2 = 16 \Leftrightarrow {x^2} + {y^2} - 2y - 3 = 0 \Leftrightarrow {x^2} + {\left( {y - 1} \right)^2} = 4 \Leftrightarrow \left\{ \begin{array}{l}x = 2\sin t\\y = 2\cos t + 1\end{array} \right..$

Khi đó ${\left| z \right|^2} = {x^2} + {y^2} = 4{\sin ^2}t + {\left( {2\cos t + 1} \right)^2} = 4\cos t + 5$ mà $\cos t \in \left[ { - \,1;1} \right]$$ \Rightarrow \,\,4\cos t + 5 \in \left[ {1;9} \right].$

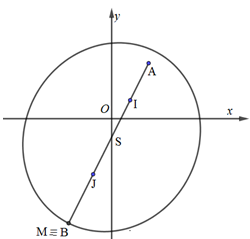
Gọi $I\left( {1;1} \right),\,\,J( - 1; - 3),\,\,A(2;3)$. Xét số phức $z = x + yi,\,\,\left( {x,y \in R} \right)$, có điểm biểu diễn là $M(x;y)$.

$\left| {z - 1 - i} \right| + \left| {z + 1 + 3i} \right| = 6\sqrt 5 $

$ \Leftrightarrow \sqrt {{{(x - 1)}^2} + {{(y - 1)}^2}}  + \sqrt {{{(x + 1)}^2} + {{(y + 3)}^2}}  = 6\sqrt 5 $ (1)

$ \Leftrightarrow MI + MJ = 6\sqrt 5  \Rightarrow M$di chuyển trên đường elip có tiêu điểm $I$ và $J$, độ dài trục lớn là $3\sqrt 5 $ (như hình vẽ).

Tìm giá trị lớn nhất của $\left| {z - 2 - 3i} \right|$ tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.

Ta có: $\overrightarrow {IA}  = (1;2),\,\,\overrightarrow {JA}  = (3;6) \Rightarrow \overrightarrow {JA}  = 3\overrightarrow {IA} $, điểm A nằm trên trục lớn của elip.

$ \Rightarrow AM$ đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.

Gọi S là trung điểm của IJ $ \Rightarrow S\left( {0; - 1} \right)$.

Độ dài đoạn $AB = SA + SB$

Mà $\overrightarrow {AS}  = \left( { - 2; - 4} \right) \Rightarrow AS = 2\sqrt 5 $,  $SB = \dfrac{{6\sqrt 5 }}{2} = 3\sqrt 5 $$ \Rightarrow AB = 5\sqrt 5 $

Vậy ${\left| {z - 2 - 3i} \right|_{\max }} = 5\sqrt 5 $.

Do tập hợp các điểm biểu diễn số phức ${\rm{w  =  }}{{\rm{z}}_1}z - {z_2}$ là đường tròn tâm là gốc tọa độ và bán kính bằng $1$ nên $\left| w \right| = 1$.

Ta có:

${\rm{w  =  }}{{\rm{z}}_1}z - {z_2},\,\,\left( {{z_1} \ne 0} \right) \Rightarrow z = \dfrac{{{\rm{w}}\,}}{{{z_1}}} + \dfrac{{{z_2}}}{{{z_1}}} \Leftrightarrow z - \dfrac{{{z_2}}}{{{z_1}}} = \dfrac{{{\rm{w}}\,}}{{{z_1}}}$

Lấy mô đun hai vế ta được \(\left| {z - \dfrac{{{z_2}}}{{{z_1}}}} \right| = \left| {\dfrac{w}{{{z_1}}}} \right| = \dfrac{1}{{\left| {{z_1}} \right|}}\)

Vậy tập hợp các điểm biểu diễn số phức $z$ là đường tròn tâm là điểm biểu diễn số phức $\dfrac{{{z_2}}}{{{z_1}}}$ và bán kính bằng $\dfrac{1}{{\left| {{z_1}} \right|}}$.

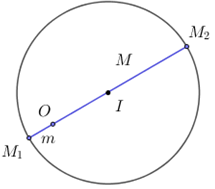
Giả sử điểm \(M\left( {x;\;y} \right)\) biểu diễn số phức \(z \Rightarrow z = x + yi \Rightarrow \left| z \right| = \sqrt {{x^2} + {y^2}} .\)

Ta có: \(\left| {2z - 3 - 4i} \right| = 10 \Leftrightarrow \left| {z - \dfrac{3}{2} - 2i} \right| = 5 \Leftrightarrow {\left( {x - \dfrac{3}{2}} \right)^2} + {\left( {y - 2} \right)^2} = 25.\)

\( \Rightarrow M\) thuộc đường tròn tâm \(I\left( {\dfrac{3}{2};\;2} \right)\) và bán kính \(R = 5.\) 

\( \Rightarrow \left| z \right| = \sqrt {{x^2} + {y^2}}  = OM.\) Ta đưa bài toán về tìm min và max của \(OM.\)

Ta có: \(OI = \sqrt {{{\left( {\dfrac{3}{2}} \right)}^2} + {2^2}}  = \dfrac{5}{2} < R \Rightarrow I\) nằm trong đường tròn.

\( \Rightarrow OM\) đạt Max và Min khi \(M \in \) đường thẳng đi qua \(O,\;I.\)

\(\begin{array}{l} \Rightarrow M = Max\;OM = R + OI = 5 + \dfrac{5}{2} = \dfrac{{15}}{2}\\m = Min\;\;OM = R - OI = 5 - \dfrac{5}{2} = \dfrac{5}{2}.\\ \Rightarrow M - m = \dfrac{{15}}{2} - \dfrac{5}{2} = 5.\end{array}\)

Đặt \(\left( {z - i} \right)\left( {i + 1} \right) = x + yi \Rightarrow \left[ \begin{array}{l}z - i = \dfrac{{x + yi}}{{i + 1}}\\z + i = \dfrac{{x + yi}}{{i + 1}} + 2i = \dfrac{{x + yi - 2 + 2i}}{{i + 1}} = \dfrac{{x - 2 + \left( {y + 2} \right)i}}{{i + 1}}\end{array} \right.\)

\( \Rightarrow \left[ \begin{array}{l}\left| {z - i} \right| = \dfrac{{\sqrt {{x^2} + {y^2}} }}{{\sqrt 2 }}\\\left| {z + i} \right| = \dfrac{{\sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y + 2} \right)}^2}} }}{{\sqrt 2 }}\end{array} \right. \Rightarrow \dfrac{{\sqrt {{x^2} + {y^2}} }}{{\sqrt 2 }} + \dfrac{{\sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y + 2} \right)}^2}} }}{{\sqrt 2 }} = 6\,\,\left( * \right)\)

Gọi \(M\left( {x;y} \right);\,\,I\left( {2; - 2} \right)\), từ (*) ta có \(\dfrac{{MO}}{{\sqrt 2 }} + \dfrac{{MI}}{{\sqrt 2 }} = 6 \Leftrightarrow MO + MI = 6\sqrt 2 \)

Do đó quỹ tích điểm M là elip nhận O; I là hai tiêu điểm và trục lớn \(2a = 6\sqrt 2  \Rightarrow a = 3\sqrt 2 \).

\(2c = OI = 2\sqrt 2  \Rightarrow c = \sqrt 2  \Rightarrow b = \sqrt {{a^2} - {c^2}}  = 4\).

Vậy diện tích elip là \(S = \pi ab = \pi .4.3\sqrt 2  = 12\pi \sqrt 2 \)