Câu hỏi:
2 năm trước
Cho số phức $z$ thỏa mãn điều kiện $\left| {z - 1 - i} \right| + \left| {z + 1 + 3i} \right| = 6\sqrt 5 $. Giá trị lớn nhất của $\left| {z - 2 - 3i} \right|$ là
Trả lời bởi giáo viên
Đáp án đúng: d
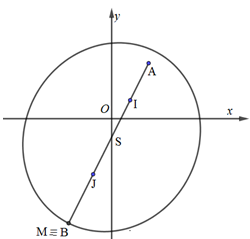
Gọi $I\left( {1;1} \right),\,\,J( - 1; - 3),\,\,A(2;3)$. Xét số phức $z = x + yi,\,\,\left( {x,y \in R} \right)$, có điểm biểu diễn là $M(x;y)$.
$\left| {z - 1 - i} \right| + \left| {z + 1 + 3i} \right| = 6\sqrt 5 $
$ \Leftrightarrow \sqrt {{{(x - 1)}^2} + {{(y - 1)}^2}} + \sqrt {{{(x + 1)}^2} + {{(y + 3)}^2}} = 6\sqrt 5 $ (1)
$ \Leftrightarrow MI + MJ = 6\sqrt 5 \Rightarrow M$di chuyển trên đường elip có tiêu điểm $I$ và $J$, độ dài trục lớn là $3\sqrt 5 $ (như hình vẽ).
Tìm giá trị lớn nhất của $\left| {z - 2 - 3i} \right|$ tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
Ta có: $\overrightarrow {IA} = (1;2),\,\,\overrightarrow {JA} = (3;6) \Rightarrow \overrightarrow {JA} = 3\overrightarrow {IA} $, điểm A nằm trên trục lớn của elip.
$ \Rightarrow AM$ đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
Gọi S là trung điểm của IJ $ \Rightarrow S\left( {0; - 1} \right)$.
Độ dài đoạn $AB = SA + SB$
Mà $\overrightarrow {AS} = \left( { - 2; - 4} \right) \Rightarrow AS = 2\sqrt 5 $, $SB = \dfrac{{6\sqrt 5 }}{2} = 3\sqrt 5 $$ \Rightarrow AB = 5\sqrt 5 $
Vậy ${\left| {z - 2 - 3i} \right|_{\max }} = 5\sqrt 5 $.
Hướng dẫn giải:
- Biểu diễn số phức và giải bài toán tìm GTLN trên mặt phẳng tọa độ
Câu hỏi khác
- Bài tập số phức và các phép toán cộng, trừ, nhân, chia số phức toán 12 có lời giải
- Bài tập phương trình bậc hai với hệ số thực (căn bậc hai của số phức) toán 12 có lời giải
- Bài tập điểm biểu diễn số phức thỏa mãn điều kiện cho trước có lời giải MÔN TOÁN Lớp 12
- Bài tập tìm min, max liên quan đến số phức có lời giải MÔN TOÁN Lớp 12
- Bài tập dạng lượng giác của số phức toán 12 có lời giải
