Tích phân (phương pháp đổi biến)

Đặt $t = f\left( x \right) \Rightarrow dt = f'\left( x \right)dx$

Đổi cận: $\left\{ \begin{array}{l}x = a \Rightarrow t = f\left( a \right)\\x = b \Rightarrow t = f\left( b \right)\end{array} \right.$

Khi đó $I = \int\limits_{f\left( a \right)}^{f\left( b \right)} {{e^t}dt}  = 0$ (Vì $f\left( a \right) = f\left( b \right)$)

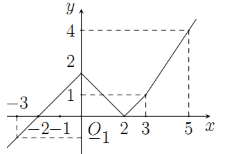
Đặt $2x - 1 = t \Rightarrow 2dx = dt$. Đổi cận $\left\{ \begin{array}{l}x =  - 1 \Rightarrow t =  - 3\\x = 3 \Rightarrow t = 5\end{array} \right.$.

Khi đó: $I = \int\limits_{ - 1}^3 {f\left( {2x - 1} \right)dx}  = \int\limits_{ - 3}^5 {f\left( t \right)\dfrac{1}{2}dt}  = \dfrac{1}{2}\int\limits_{ - 3}^5 {f\left( t \right)dt}$

               $\begin{array}{l} = \dfrac{1}{2}\left( {\int\limits_{ - 3}^{ - 2} {f\left( x \right)dx}  + \int\limits_{ - 2}^0 {f\left( x \right)dx}  + \int\limits_0^2 {f\left( x \right)dx}  + \int\limits_2^3 {f\left( x \right)dx}  + \int\limits_3^5 {f\left( x \right)dx} } \right)\\ = \dfrac{1}{2}\left( { - {S_{\Delta ABC}} + {S_{\Delta OCD}} + {S_{\Delta OED}} + {S_{\Delta EFI}} + {S_{IFHK}}} \right)\\ = \dfrac{1}{2}\left( { - \dfrac{1}{2} + 2 + 2 + \dfrac{1}{2} + 5} \right) = \dfrac{9}{2}.\end{array}$

Bước 1: Biểu diễn $\left( {6{x^2} + 2x} \right)f\left( {2{x^3} + {x^2} + 1} \right)$

Khi $x \ge 0$, ta có:

$f\left( {2{x^3} + {x^2} + 1} \right) = x + 2$$\Leftrightarrow \left( {6{x^2} + 2x} \right)f\left( {2{x^3} + {x^2} + 1} \right)$$= \left( {6{x^2} + 2x} \right)(x + 2)(*)$

Bước 2: Sử dụng phương pháp đổi biến số tính $\int_1^4 f (x)dx$

Lấy tích phân từ 0 đến 1 hai vế của $(*)$ ta được

$\int_0^1 {\left( {6{x^2} + 2x} \right)} f\left( {2{x^3} + {x^2} + 1} \right)dx$$= \int_0^1 {\left( {6{x^2} + 2x} \right)\left( {x + 2} \right)dx}$

$\Leftrightarrow \int_0^1 f \left( {2{x^3} + {x^2} + 1} \right){\rm{d}}\left( {2{x^3} + {x^2} + 1} \right)$$= \dfrac{{49}}{6}$

Đặt $t = 2{x^3} + {x^2} + 1$

Đổi cận:$x = 0 \Rightarrow t = 1;x = 1 \Rightarrow t = 4$

$\Rightarrow \int_1^4 f (t)dt = \dfrac{{49}}{6} \Leftrightarrow \int_1^4 f (x)dx = \dfrac{{49}}{6}$

Dựa vào các đáp án, xét:

$\int\limits_{ - 1}^2 {f(2x)dx}$$= \dfrac{1}{2}\int\limits_{ - 1}^2 {f(2x)d(2x)}$$= \dfrac{1}{2}\int\limits_{ - 2}^4 {f(x)dx }$$= 1$

$\begin{array}{l}\int\limits_{ - 3}^3 {f(x + 1)dx}  = \int\limits_{ - 3}^3 {f(x + 1)d(x + 1)} \\ = \int\limits_{ - 2}^4 {f(x)dx = 2} \end{array}$

$\int\limits_0^6 {\dfrac{1}{2}f(x - 2)dx}  = \int\limits_0^6 {\dfrac{1}{2}f(x - 2)d(x - 2)}$$= \dfrac{1}{2}\int\limits_{ - 2}^4 {f(x)dx = 1}$

Do đó các đáp án B, C, D đều đúng, đáp án A sai.

Xét $\int\limits_0^1 {xf\left( {3x} \right)dx = 1}$.

Đặt $t = 3x \Leftrightarrow dt = 3dx$. Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 0\\x = 1 \Rightarrow t = 3\end{array} \right.$.

$\Rightarrow \int\limits_0^1 {xf\left( {3x} \right)dx}  = 1 \Leftrightarrow \int\limits_0^3 {\dfrac{t}{3}f\left( t \right)\dfrac{{dt}}{3}}  = 1$$\Leftrightarrow \dfrac{1}{9}\int\limits_0^3 {tf\left( t \right)dt}  = 1$

$\Leftrightarrow \int\limits_0^3 {tf\left( t \right)dt}  = 9 \Leftrightarrow 2\int\limits_0^3 {xf\left( x \right)dx}  = 18$$\Rightarrow \int\limits_0^3 {2xf\left( x \right)dx}  = 18$

Ta có: $\int\limits_0^3 {\left[ {{x^2}f'\left( x \right) + 2xf\left( x \right)} \right]dx}$$= \int\limits_0^3 {{x^2}f'\left( x \right)dx}  + \int\limits_0^3 {2xf\left( x \right)dx}$

$\begin{array}{l} \Leftrightarrow \int\limits_0^3 {\left( {{x^2}f\left( x \right)} \right)'dx}  = \int\limits_0^3 {{x^2}f'\left( x \right)dx}  + 18\\ \Leftrightarrow \left. {{x^2}f\left( x \right)} \right|_0^3 = \int\limits_0^3 {{x^2}f'\left( x \right)dx}  + 18\\ \Leftrightarrow 9f\left( 3 \right) = \int\limits_0^3 {{x^2}f'\left( x \right)dx}  + 18\\ \Leftrightarrow 9.1 = \int\limits_0^3 {{x^2}f'\left( x \right)dx}  + 18\\ \Leftrightarrow \int\limits_0^3 {{x^2}f'\left( x \right)dx}  = 9 - 18 =  - 9\end{array}$

Đặt $t = \sqrt[3]{{1 - x}}$$\Rightarrow {t^3} = 1 - x \Rightarrow 3{t^2}dt =  - dx \Leftrightarrow dx =  - 3{t^2}dt$

Với $x = 0 \Rightarrow t = 1$ ; $x = 1 \Rightarrow t = 0$

Khi đó $I = \int\limits_1^0 {t.\left( { - 3{t^2}} \right)\,dt}  = 3\int\limits_0^1 {{t^3}dt}$

Bước 1:

Đặt $x = 4\sin t$

Bước 2:

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow \sin t = 0 \Rightarrow t = 0\\x = \sqrt 8  \Rightarrow \sin t = \dfrac{{\sqrt 2 }}{2} \Rightarrow t = \dfrac{\pi }{4}\end{array} \right.$

Bước 3:

Ta có: $x = 4\sin t \Rightarrow dx = d\left( {4\sin t} \right)$$= \left( {4\sin t} \right)'dt = 4\cos tdt$

Bước 4:

Khi đó ta có: $I = 4\int\limits_0^{\dfrac{\pi }{4}} {\sqrt {16 - 16{{\sin }^2}t} \cos tdt}$$= 4\int\limits_0^{\dfrac{\pi }{4}} {4.{{\cos }^2}tdt}$$= 16\int\limits_0^{\dfrac{\pi }{4}} {{{\cos }^2}tdt}$ $= 8\int\limits_0^{\dfrac{\pi }{4}} {\left( {1 + \cos 2t} \right)dt}$  

Ta có: $\int\limits_1^3 {f\left( x \right)dx = 4} .$

Đặt $2x + 1 = t \Rightarrow dt = 2dx \Rightarrow dx = \dfrac{1}{2}dt$

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 1\\x = 1 \Rightarrow t = 3\end{array} \right.$

$\Rightarrow I = \int\limits_0^1 {f\left( {2x + 1} \right)dx}  = \dfrac{1}{2}\int\limits_1^3 {f\left( t \right)dt = } \dfrac{1}{2}.4 = 2.$

Ta có

$\begin{array}{l}I = \int\limits_0^2 {\left[ {f\left( {1 - 3x} \right) + 9} \right]dx} \\ \Leftrightarrow I = \int\limits_0^2 {f\left( {1 - 3x} \right)dx}  + \int\limits_0^2 {9dx} \end{array}$

Đặt ${I_1} = \int\limits_0^2 {f\left( {1 - 3x} \right)dx}$.

Đặt $t = 1 - 3x \Rightarrow dt =  - 3dx$.

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 1\\x = 2 \Rightarrow t =  - 5\end{array} \right.$.

$\Rightarrow {I_1} =  - \dfrac{1}{3}\int\limits_1^{ - 5} {f\left( t \right).dt}  = \dfrac{1}{3}\int\limits_{ - 5}^1 {f\left( x \right)dx}  = \dfrac{1}{3}.9 = 3$.

Đặt ${I_2} = \int\limits_0^2 {9dx}  = \left. {9x} \right|_0^2 = 18$.

Vậy $I = {I_1} + {I_2} = 3 + 18 = 21.$

Ta có: $\int\limits_0^1 {f\left( x \right)} dx = 4$ và $\int\limits_0^1 {f\left( {3x} \right)dx = 6.}$

Đặt $t = 3x \Rightarrow dt = 3dx \Rightarrow dx = \dfrac{1}{3}dt$

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 0\\x = 1 \Rightarrow t = 3\end{array} \right.$

$\begin{array}{l} \Rightarrow \int\limits_0^1 {f\left( {3x} \right)dx = 6} \\ \Leftrightarrow \int\limits_0^3 {\dfrac{1}{3}f\left( t \right)dt}  = 6\\ \Leftrightarrow \int\limits_0^3 {f\left( t \right)dt}  = 18\\ \Rightarrow \int\limits_0^3 {f\left( x \right)dx}  = 18\\ \Rightarrow \int\limits_1^3 {f\left( x \right)dx}  = \int\limits_0^3 {f\left( x \right)dx}  - \int\limits_0^1 {f\left( x \right)dx} \\ \Leftrightarrow \int\limits_1^3 {f\left( x \right)dx}  = 18 - 4 = 14.\end{array}$

Đặt $t = \sqrt {{x^2} + 9}  \Rightarrow {t^2} = {x^2} + 9$ $\Rightarrow tdt = xdx$.

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 3\\x = 4 \Rightarrow t = 5\end{array} \right.$.

Vậy $I = \int\limits_0^4 {x\sqrt {{x^2} + 9} dx}  = \int\limits_3^5 {t.tdt}  = \int\limits_3^5 {{t^2}dt}$.

Đặt $t = \sqrt {1 + 3\ln x}  \Rightarrow {t^2} = 1 + 3\ln x \Rightarrow 2tdt = \dfrac{3}{x}dx \Rightarrow \dfrac{1}{x}dx = \dfrac{2}{3}tdt$

Đổi cận:  $\left\{ \begin{array}{l}x = 1 \Rightarrow t = 1\\x = e \Rightarrow t = 2\end{array} \right.$.

Khi đó ta có: $I = \int\limits_1^2 {t.\dfrac{2}{3}tdt}  = \dfrac{2}{3}\int\limits_1^2 {{t^2}dt}$

Ta có: $I = \int\limits_0^3 {\dfrac{x}{{1 + \sqrt {x + 1} }}dx}$

Đặt $t = \sqrt {x + 1}$ $\Rightarrow {t^2} = x + 1 \Rightarrow dx = 2tdt$

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 1\\x = 3 \Rightarrow t = 2\end{array} \right.$

$\Rightarrow I = \int\limits_0^2 {\dfrac{{{t^2} - 1}}{{1 + t}}2tdt}$ $= 2\int\limits_0^2 {\dfrac{{\left( {t - 1} \right)\left( {t + 1} \right)}}{{t + 1}}tdt}$$= 2\int\limits_0^2 {t\left( {t - 1} \right)dt = 2\int\limits_0^2 {\left( {{t^2} - t} \right)dt} }$

$\Rightarrow f\left( t \right) = 2\left( {{t^2} - t} \right) = 2{t^2} - 2t.$

Đặt $t = {e^x} + 1 \Rightarrow dt = {e^x}dx$.

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 2\\x = \ln 2 \Rightarrow t = 3\end{array} \right.$.

Khi đó ta có

$\begin{array}{l}\int\limits_0^{\ln 2} {\dfrac{{{e^{2x}}}}{{{e^x} + 1}}dx}  = \int\limits_0^{\ln 2} {\dfrac{{{e^x}}}{{{e^x} + 1}}.{e^x}dx}  = \int\limits_2^3 {\dfrac{{t - 1}}{t}dt} \\ = \int\limits_2^3 {\left( {1 - \dfrac{1}{t}} \right)dt}  = \left. {\left( {t - \ln t} \right)} \right|_2^3 = 1 - \ln 3 + \ln 2 = 1 + \ln \dfrac{2}{3}\\ \Rightarrow a = 1,\,\,b = 2,\,\,c = 3\end{array}$

Vậy $a - b + c = 1 - 2 + 3 = 2.$

Lấy tích phân từ 0 đến 1 hai vế ta được:

$\int\limits_0^1 {f\left( x \right)dx}  + \int\limits_0^1 {\left( {5x - 2} \right)f\left( {5{x^2} - 4x} \right)dx}  = \int\limits_0^1 {\left( {50{x^3} - 60{x^2} + 23x - 1} \right)dx}$

Xét tích phân $I = \int\limits_0^1 {\left( {5x - 2} \right)f\left( {5{x^2} - 4x} \right)dx}$.

Đặt $t = 5{x^2} - 4x$ ta có $dt = \left( {10x - 4} \right)dx \Leftrightarrow \left( {5x - 2} \right)dx = \dfrac{1}{2}dt$.

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 0\\x = 1 \Rightarrow t = 1\end{array} \right.$.

$\Rightarrow I = \int\limits_0^1 {\dfrac{1}{2}f\left( t \right)dt}  = \dfrac{1}{2}\int\limits_0^1 {f\left( x \right)dx}$

Xét tích phân $J = \int\limits_0^1 {\left( {50{x^3} - 60{x^2} + 23x - 1} \right)dx}$ ta có: $J = \left. {\left( {\dfrac{{50{x^4}}}{4} - \dfrac{{60{x^3}}}{3} + \dfrac{{23{x^2}}}{2} - x} \right)} \right|_0^1 = 3$

Khi đó ta có $\int\limits_0^1 {f\left( x \right)dx}  + \dfrac{1}{2}\int\limits_0^1 {f\left( x \right)dx}  = 3$ $\Leftrightarrow \dfrac{3}{2}\int\limits_0^1 {f\left( x \right)dx}  = 3$ $\Leftrightarrow \int\limits_0^1 {f\left( x \right)dx}  = 2$.

Theo bài ra ta có

$\begin{array}{l}f\left( {{x^2} + 3x + 1} \right) = x + 2\\ \Rightarrow f\left( {{x^2} + 3x + 1} \right)\left( {2x + 3} \right) = \left( {x + 2} \right)\left( {2x + 3} \right)\\ \Rightarrow \int\limits_0^1 {f\left( {{x^2} + 3x + 1} \right)\left( {2x + 3} \right)dx}  = \int\limits_0^1 {\left( {x + 2} \right)\left( {2x + 3} \right)dx} \\ \Rightarrow \int\limits_0^1 {f\left( {{x^2} + 3x + 1} \right)\left( {2x + 3} \right)dx}  = \dfrac{{61}}{6}\end{array}$

Đặt $t = {x^2} + 3x + 1 \Rightarrow dt = \left( {2x + 3} \right)dx$.

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 1\\x = 1 \Rightarrow t = 5\end{array} \right.$.

$\Rightarrow \int\limits_0^1 {f\left( {{x^2} + 3x + 1} \right)\left( {2x + 3} \right)dx}  = \int\limits_1^5 {f\left( t \right)dt}  = \int\limits_1^5 {f\left( x \right)dx}$.

Vậy $\int\limits_1^5 {f\left( x \right)dx}  = \dfrac{{61}}{6}$.

Đặt $t = 3 - 2x \Rightarrow dt =  - 2dx$. Đổi cận $\left\{ \begin{array}{l}x =  - 2 \Rightarrow t = 7\\x = 3 \Rightarrow t =  - 3\end{array} \right.$.

Khi đó ta có:

$\begin{array}{l}I =  - \dfrac{1}{2}\int\limits_7^{ - 3} {f\left( {\left| t \right|} \right)dt}  = \dfrac{1}{2}\int\limits_{ - 3}^7 {f\left( {\left| t \right|} \right)dt} \\\,\,\,\, = \dfrac{1}{2}\left( {\int\limits_{ - 3}^0 {f\left( { - t} \right)dt}  + \int\limits_0^7 {f\left( t \right)dt} } \right)\\\,\,\,\, = \dfrac{1}{2}\left( { - \int\limits_3^0 {f\left( x \right)dx}  + \int\limits_0^7 {f\left( x \right)dx} } \right)\\\,\,\,\, = \dfrac{1}{2}\left( {\int\limits_0^3 {f\left( x \right)dx}  + \int\limits_0^7 {f\left( x \right)dx} } \right)\\\,\,\,\, = \dfrac{1}{2}\left( {6 + 10} \right) = 8\end{array}$.

Đặt $t = \sin x \Rightarrow dt = \cos xdx$.

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 0\\x = \dfrac{\pi }{2} \Rightarrow t = 1\end{array} \right.$, khi đó

$\begin{array}{l}\int\limits_0^{\frac{\pi }{2}} {\dfrac{{\cos x}}{{{{\sin }^2}x - 5\sin x + 6}}dx}  = \int\limits_0^1 {\dfrac{{dt}}{{{t^2} - 5t + 6}}} \\ = \int\limits_0^1 {\dfrac{{dt}}{{\left( {t - 2} \right)\left( {t - 3} \right)}}}  = \int\limits_0^1 {\left( {\dfrac{1}{{t - 3}} - \dfrac{1}{{t - 2}}} \right)dt} \\ = \left. {\left( {\ln \left| {t - 3} \right| - \ln \left| {t - 2} \right|} \right)} \right|_0^1 = \left. {\ln \left| {\dfrac{{t - 3}}{{t - 2}}} \right|} \right|_0^1\\ = \ln 2 - \ln \dfrac{3}{2} = \ln \dfrac{4}{3}\end{array}$

$\Rightarrow a = 1,\,\,b = 3$.

Vậy $a + b = 1 + 3 = 4$.

$\begin{array}{l}\int\limits_0^1 {\dfrac{{xdx}}{{{{\left( {x + 2} \right)}^2}}} = \int\limits_0^1 {\dfrac{{x + 2}}{{{{\left( {x + 2} \right)}^2}}}dx}  - \int\limits_0^1 {\dfrac{2}{{{{\left( {x + 2} \right)}^2}}}dx} }  \\= \left. {\left( {\ln \left| {x + 2} \right| + \dfrac{2}{{x + 2}}} \right)} \right|_0^1\\ = \ln 3 + \dfrac{2}{3} - \ln 2 - 1 = \ln 3 - \ln 2 - \dfrac{1}{3}\\ \Rightarrow \left\{ \begin{array}{l}a =  - \dfrac{1}{3}\\b =  - 1\\c = 1\end{array} \right. \Rightarrow 3a + b + c = 3.\left( { - \dfrac{1}{3}} \right) - 1 + 1 =  - 1.\end{array}$

$I = \int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{3}} {\dfrac{{{{\cos }^2}x + \sin x\cos x + 1}}{{{{\cos }^4}x + \sin x{{\cos }^3}x}}dx}  = \int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{3}} {\dfrac{{1 + \tan x + 1 + {{\tan }^2}x}}{{{{\cos }^2}x\left( {1 + \tan x} \right)}}dx}  = \int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{3}} {\dfrac{{{{\tan }^2}x + \tan x + 2}}{{{{\cos }^2}x\left( {1 + \tan x} \right)}}dx}$

Đặt $t = \tan x \Rightarrow dt = \dfrac{1}{{{{\cos }^2}x}}dx$. Đổi cận $\left\{ \begin{array}{l}x = \dfrac{\pi }{4} \Rightarrow t = 1\\x = \dfrac{\pi }{3} \Rightarrow t = \sqrt 3 \end{array} \right.$.

$\begin{array}{l} \Rightarrow I = \int\limits_1^{\sqrt 3 } {\dfrac{{{t^2} + t + 2}}{{t + 1}}dt}  = \int\limits_1^{\sqrt 3 } {\left( {t + \dfrac{2}{{t + 1}}} \right)dt} \\ = \left. {\dfrac{{{t^2}}}{2} + 2\ln \left| {t + 1} \right|} \right|_1^{\sqrt 3 } = \dfrac{3}{2} + 2\ln \left( {\sqrt 3  + 1} \right) - \dfrac{1}{2} - 2\ln 2 = 1 - 2\ln 2 + 2\ln \left( {1 + \sqrt 3 } \right)\\ \Rightarrow \left\{ \begin{array}{l}a = 1\\b =  - 2\\c = 2\end{array} \right. \Rightarrow abc = 1.\left( { - 2} \right).2 =  - 4\end{array}$