Câu hỏi:
2 năm trước
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Tính tích phân \(I = \int\limits_{ - 1}^3 {f\left( {2x - 1} \right)dx} \).
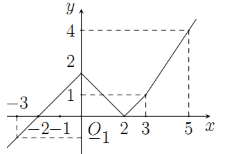
Trả lời bởi giáo viên
Đáp án đúng: d
Đặt \(2x - 1 = t \Rightarrow 2dx = dt\). Đổi cận \(\left\{ \begin{array}{l}x = - 1 \Rightarrow t = - 3\\x = 3 \Rightarrow t = 5\end{array} \right.\).
Khi đó: \(I = \int\limits_{ - 1}^3 {f\left( {2x - 1} \right)dx} = \int\limits_{ - 3}^5 {f\left( t \right)\dfrac{1}{2}dt} = \dfrac{1}{2}\int\limits_{ - 3}^5 {f\left( t \right)dt} \)
\(\begin{array}{l} = \dfrac{1}{2}\left( {\int\limits_{ - 3}^{ - 2} {f\left( x \right)dx} + \int\limits_{ - 2}^0 {f\left( x \right)dx} + \int\limits_0^2 {f\left( x \right)dx} + \int\limits_2^3 {f\left( x \right)dx} + \int\limits_3^5 {f\left( x \right)dx} } \right)\\ = \dfrac{1}{2}\left( { - {S_{\Delta ABC}} + {S_{\Delta OCD}} + {S_{\Delta OED}} + {S_{\Delta EFI}} + {S_{IFHK}}} \right)\\ = \dfrac{1}{2}\left( { - \dfrac{1}{2} + 2 + 2 + \dfrac{1}{2} + 5} \right) = \dfrac{9}{2}.\end{array}\)
Hướng dẫn giải:
Sử dụng phương pháp đổi biến tính tích phân.
Câu hỏi khác
- Bài tập nguyên hàm toán 12 có lời giải
- Bài tập tích phân các hàm số cơ bản toán 12 có lời giải
- Bài tập tích phân có lời giải MÔN TOÁN Lớp 12
- Bài tập sử dụng phương pháp từng phần để tìm nguyên hàm có lời giải MÔN TOÁN Lớp 12
- Bài tập sử dụng phương pháp đổi biến để tìm nguyên hàm có lời giải MÔN TOÁN Lớp 12
