Số đường tiệm cận của đồ thị hàm số \(y = \dfrac{{{x^2} - x + 1}}{{{x^2} - x - 2}}\) là
Ta có:
\(\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{{x^2} - x + 1}}{{{x^2} - x - 2}} = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{1 - \dfrac{1}{x} + \dfrac{1}{{{x^2}}}}}{{1 - \dfrac{1}{x} - \dfrac{2}{{{x^2}}}}} = 1 \Rightarrow y = 1\) là TCN của đồ thị hàm số.
\(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to 2} y = \mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} - x + 1}}{{{x^2} - x - 2}} = \infty \\\mathop {\lim }\limits_{x \to - 1} y = \mathop {\lim }\limits_{x \to - 1} \dfrac{{{x^2} - x + 1}}{{{x^2} - x - 2}} = \infty \end{array} \right. \Rightarrow x = 2,\,\,x = - 1\) là các đường TCĐ của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{3x + 2}}{{x - 2}}\) là đường thẳng có phương trình:
TXĐ: \(D = \mathbb{R}\backslash 2\). Ta có:
\(\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} \dfrac{{3x + 2}}{{x - 2}} = + \infty \)\( = > \)Tiệm cận \(x = 2\)
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{2x + 1}}{{x - 2}}\) là đường thẳng có phương trình:
Đồ thị hàm số \(y = \dfrac{{2x - 1}}{{x - 1}}\) có TCĐ \(x = 2\).
Đề thi THPT QG – 2021 lần 1– mã 104
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{x - 1}}{{x + 2}}\) là đường thẳng có phương trình:\(\)
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{x - 1}}{{x + 2}}\) là \(x = - 2\)
Đề thi THPT QG 2019 – mã đề 104
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau :

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
Dựa vào đồ thị hàm số ta thấy:
\(\mathop {\lim }\limits_{x \to - \infty } y = 0;\,\,\mathop {\lim }\limits_{x \to + \infty } y = 3 \Rightarrow \) Đồ thị hàm số có 2 tiệm cận ngang \(y = 0\) và \(y = 3\).
\(\mathop {\lim }\limits_{x \to {0^ + }} y = + \infty \Rightarrow \) Đồ thị hàm số có đường tiệm cận đứng \(x = 0\).
Vậy đồ thị hàm số đã cho có tất cả 3 đường tiệm cận.
Cho hàm số \(y = \dfrac{{x - 3}}{{{x^3} - 3m{x^2} + \left( {2{m^2} + 1} \right)x - m}}\). Có bao nhiêu giá trị nguyên thuộc đoạn \(\left[ { - 6;\,6} \right]\) của tham số \(m\) để đồ thị hàm số có bốn đường tiệm cận?
Ta có \(y = \dfrac{{x - 3}}{{{x^3} - 3m{x^2} + \left( {2{m^2} + 1} \right)x - m}}\)
\(\mathop {\lim }\limits_{x \to \pm \infty } \,f\left( x \right) = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{x - 3}}{{{x^3} - 3m{x^2} + \left( {2{m^2} + 1} \right)x - m}} = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{\dfrac{x}{{{x^3}}} - \dfrac{3}{{{x^3}}}}}{{1 - 3m\dfrac{{{x^2}}}{{{x^3}}} + \left( {2{m^2} + 1} \right)\dfrac{x}{{{x^3}}} - \dfrac{m}{{{x^3}}}}} = 0\) nên \(y = 0\) là tiệm cận ngang của đồ thị hàm số.
Vậy để đồ thị hàm số có 4 đường tiệm cận thì đồ thị hàm số phải có 3 đường tiệm cận đứng.
Hay phương trình \({x^3} - 3m{x^2} + \left( {2{m^2} + 1} \right)x - m = 0\,\,\left( 1 \right)\) có ba nghiệm phân biệt \(x \ne 3.\)
Ta có \({x^3} - 3m{x^2} + \left( {2{m^2} + 1} \right)x - m = 0 \Leftrightarrow \left( {x - m} \right)\left( {{x^2} - 2mx + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = m\\{x^2} - 2mx + 1 = 0\,\left( * \right)\end{array} \right.\)
Để phương trình (1) có ba nghiệm phân biệt khác 3 thì \(m \ne 3\) và phương trình (*) có hai nghiệm phân biệt khác \(m\) và khác \(3.\)
Do đó \(\left\{ \begin{array}{l}\Delta ' = {m^2} - 1 > 0\\{3^2} - 2.m.3 + 1 \ne 0\\{m^2} - 2{m^2} + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m < - 1\\m > 1\end{array} \right.\\m \ne \dfrac{5}{3}\\m \ne - 1\\m \ne 1\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m < - 1\\m > 1\end{array} \right.\\m \ne \dfrac{5}{3}\end{array} \right.\)
Kết hợp điều kiện \(\left\{ \begin{array}{l}m \ne 3\\ - 6 \le m \le 6\end{array} \right. \Rightarrow m \in \left\{ { - 6; - 5; - 4; - 3; - 2;2;4;5;6} \right\}\)
Vậy có 9 giá trị của m thỏa mãn điều kiện
Cho đồ thị hàm số \(y = \dfrac{{{x^2} - 3x + 2}}{{{x^2} - 1}}\,\,\left( C \right)\). Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị \(\left( C \right)\) là:
Ta có:
\(\mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{{x^2} - 3x + 2}}{{{x^2} - 1}}\)\( = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{{x^2}\left( {1 - \dfrac{3}{x} + \dfrac{2}{{{x^2}}}} \right)}}{{{x^2}\left( {1 - \dfrac{1}{{{x^2}}}} \right)}}\)\( = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{1 - \dfrac{3}{x} + \dfrac{2}{{{x^2}}}}}{{1 - \dfrac{1}{{{x^2}}}}} = 1\)
Nên đường thẳng \(y = 1\) là tiệm cận ngang của đồ thị hàm số đã cho
Ta có: \(\mathop {\lim }\limits_{x \to 1} \dfrac{{{x^2} - 3x + 2}}{{{x^2} - 1}}\)\( = \mathop {\lim }\limits_{x \to 1} \dfrac{{\left( {x - 1} \right)\left( {x - 2} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)\( = \mathop {\lim }\limits_{x \to 1} \dfrac{{x - 2}}{{x + 1}} = \dfrac{{ - 1}}{2}\)
\(\mathop {\lim }\limits_{x \to - {1^ + }} \dfrac{{{x^2} - 3x + 2}}{{{x^2} - 1}} = + \infty \) nên đường thẳng \(x = - 1\) là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 1 tiệm cận đứng và 1 tiệm cận ngang.
Gọi \(S\) là tập hợp các giá trị nguyên \(m\) để đồ thị hàm số \(y = \dfrac{{\sqrt {x + 2} }}{{\sqrt {{x^2} - 6x + 2m} }}\) có hai đường tiệm cận đứng. Số phần tử của \(S\) là:
ĐKXĐ: \(\left\{ \begin{array}{l}x + 2 \ge 0\\{x^2} - 6x + 2m > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\{x^2} - 6x + 2m > 0\end{array} \right.\).
Để đồ thị hàm số có hai đường tiệm cận đứng thì phương trình \({x^2} - 6x + 2m = 0\) có 2 nghiệm phân biệt thỏa mãn \({x_1} > {x_2} > - 2\).
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\{x_1} + {x_2} > - 4\\\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right) > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9 - 2m > 0\\6 > - 4\,\,\left( {luôn\,\,đúng} \right)\\{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) + 4 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m < \frac{9}{2}\\2m + 2.6 + 4 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < \frac{9}{2}\\2m > - 16\end{array} \right.\\ \Leftrightarrow - 8 < m < \frac{9}{2}\\ \Rightarrow S = \left\{ { - 7; - 6; - 5; - 4; - 3; - 2; - 1;0;1;2;3;4} \right\}\end{array}\)
Vậy tập hợp \(S\) có 12 phần tử.
Cho hàm số \(y = \dfrac{{\sqrt {x - 2} }}{{\left( {{x^2} - 4} \right)\left( {2x - 7} \right)}}\). Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
Xét hàm số: \(y = \dfrac{{\sqrt {x - 2} }}{{\left( {{x^2} - 4} \right)\left( {2x - 7} \right)}}\)
TXĐ: \(D = \left( {2; + \infty } \right)\backslash \left\{ {\dfrac{7}{2}} \right\}.\)
\(\mathop {\lim }\limits_{x \to \frac{7}{2}} \dfrac{{\sqrt {x - 2} }}{{\left( {{x^2} - 4} \right)\left( {2x - 7} \right)}}\) \( = \mathop {\lim }\limits_{x \to \frac{7}{2}} \dfrac{1}{{\sqrt {x - 2} \left( {x + 2} \right)\left( {2x - 7} \right)}} = \infty \) \( \Rightarrow x = \dfrac{7}{2}\) là đường TCĐ của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt {x - 2} }}{{\left( {{x^2} - 4} \right)\left( {2x - 7} \right)}} = \mathop {\lim }\limits_{x \to 2} \dfrac{1}{{\left( {x + 2} \right)\sqrt {x - 2} \left( {2x - 7} \right)}} = \infty \) \( \Rightarrow x = 2\) là đường TCĐ của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to + \infty } \dfrac{{\sqrt {x - 2} }}{{\left( {{x^2} - 4} \right)\left( {2x - 7} \right)}}\) \( = \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{\sqrt {x - 2} \left( {x + 2} \right)\left( {2x - 7} \right)}} = 0\) \( \Rightarrow y = 0\) là TCN của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có tất cả 3 đường tiệm cận.
Số đường tiệm cận của đồ thị hàm số \(y = \dfrac{{2x + 1}}{{\sqrt {{x^2} - 3} }}\) là:
Xét hàm số: \(y = \frac{{2x + 1}}{{\sqrt {{x^2} - 3} }}\) ta có:
TXĐ: \(D = \left( { - \infty ;\,\, - \sqrt 3 } \right) \cup \left( {\sqrt 3 ; + \infty } \right)\)
Ta có: \(\mathop {\lim }\limits_{x \to \sqrt 3 } \frac{{2x + 1}}{{\sqrt {{x^2} - 3} }} = + \infty \) \( \Rightarrow x = \sqrt 3 \) là TCĐ của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to - \sqrt 3 } \frac{{2x + 1}}{{\sqrt {{x^2} - 3} }} = - \infty \) \( \Rightarrow x = - \sqrt 3 \) là TCĐ của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{2x + 1}}{{\sqrt {{x^2} - 3} }} = \mathop {\lim }\limits_{x \to - \infty } \frac{{2 + \frac{1}{x}}}{{ - \sqrt {1 - \frac{3}{{{x^2}}}} }} = - 2\) \( \Rightarrow y = - 2\) là TCN của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 1}}{{\sqrt {{x^2} - 3} }} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 + \frac{1}{x}}}{{ \sqrt {1 - \frac{3}{{{x^2}}}} }} = 2\) \( \Rightarrow y = 2\) là TCN của đồ thị hàm số.
\( \Rightarrow \) Đồ thị hàm số có 4 đường tiệm cận.
Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:
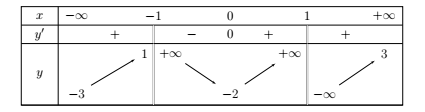
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
Dựa vào đồ thị hàm số ta thấy:
\(\mathop {\lim }\limits_{x \to - \infty } y = - 3 \Rightarrow y = - 3\) là tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to + \infty } y = 3 \Rightarrow y = 3\) là tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = + \infty \Rightarrow x = - 1\) là tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {1^ - }} y = + \infty ,\,\,\mathop {\lim }\limits_{x \to {1^ + }} y = - \infty \Rightarrow x = 1\) là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tổng 4 đường tiệm cận.
Đồ thị hàm số \(y = \dfrac{{\sqrt {{x^2} + 1} }}{{x - 1}}\) có bao nhiêu tiệm cận?
TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
Ta có:
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{\sqrt {{x^2} + 1} }}{{x - 1}} = + \infty ,\,\,\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \dfrac{{\sqrt {{x^2} + 1} }}{{x - 1}} = - \infty \)
Suy ra \(x = 1\) là tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\sqrt {{x^2} + 1} }}{{x - 1}} = 1,\,\,\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\sqrt {{x^2} + 1} }}{{x - 1}} = - 1\)
Suy ra \(y = 1,\,\,y = - 1\) là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có tất cả 3 đường tiệm cận.
Tìm tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(f\left( x \right) = \dfrac{{{x^2} - 6x + 8}}{{\left( {{x^2} - 4x + 3} \right)\sqrt {x - 2} }}\).
ĐKXĐ: \(\left\{ \begin{array}{l}{x^2} - 4x + 3 \ne 0\\x - 2 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1,\,\,x \ne 3\\x > 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 2\\x \ne 3\end{array} \right.\) \( \Rightarrow \) TXĐ: \(D = \left( {2; + \infty } \right)\backslash \left\{ 3 \right\}\).
Ta có:
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0 \Rightarrow \) Đồ thị hàm số có TCN \(y = 0\).
\(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 0 \Rightarrow \)\(x = 2\) không là TCĐ của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = - \infty \Rightarrow \) Đồ thị hàm số có TCĐ \(x = 3\).
Vậy đồ thị hàm số đã cho có tổng 2 đường tiệm cận.
Số đường tiệm cận của đồ thị hàm số \(y = \dfrac{x}{{\sqrt {{x^2} + 1} }}\) là:
TXĐ: \(D = \mathbb{R}.\)
Có: \(\sqrt {{x^2} + 1} = 0\) vô nghiệm \( \Rightarrow \) đồ thị hàm số không có TCĐ.
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \dfrac{x}{{\sqrt {{x^2} + 1} }} = \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{\sqrt {1 + \dfrac{1}{{{x^2}}}} }} = 1\) và \(\mathop {\lim }\limits_{x \to - \infty } \dfrac{x}{{\sqrt {{x^2} + 1} }} = \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{ - \sqrt {1 + \dfrac{1}{{{x^2}}}} }} = - 1.\)
Vậy đồ thị hàm số có 2 đường tiệm cận ngang.
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) thuộc \(\left[ { - 10;10} \right]\) để đồ thị hàm số \(y = \dfrac{{\sqrt {m{x^2} - 4} }}{{x - 1}}\) có ba đường tiệm cận?
ĐKXĐ: \(\left\{ \begin{array}{l}m{x^2} \ge 4\\x \ne 1\end{array} \right.\) \( \Rightarrow m > 0\).
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\sqrt {m{x^2} - 4} }}{{x - 1}} = \sqrt m \\\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\sqrt {m{x^2} - 4} }}{{x - 1}} = - \sqrt m \end{array} \right. \Rightarrow \) Đồ thị hàm số có 2 đường tiệm cận ngang \(y = \pm \sqrt m \) \(\left( {m > 0} \right)\).
Để đồ thị hàm số \(y = \dfrac{{\sqrt {m{x^2} - 4} }}{{x - 1}}\) có 3 đường tiệm cận thì đồ thị hàm số phải có 1 đường tiệm cận đứng.
\( \Rightarrow x = 1\) phải thỏa mãn điều kiện \(m{x^2} \ge 4 \Leftrightarrow m \ge 4\).
Do đó, \(m \ge 4\) thì hàm số đã cho có 1 đường tiệm cận đứng và 2 đường tiệm cận ngang.
Mặt khác \(m \in \left[ { - 10;10} \right]\), \(m \in \mathbb{Z}\) nên \(m \in \left\{ {4;5;6;7;8;9;10} \right\}\).
Vậy có tất cả 7 giá trị nguyên của tham số \(m\) thỏa mãn bài toán.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
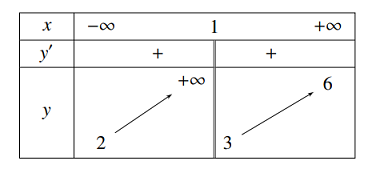
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:
Từ BBT của hàm số đã cho ta có:
+) \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2;\,\,\,\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 6\) nên đồ thị hàm số đã cho có 2 đường tiệm cận ngang là \(y = 2;\,\,y = 6\).
+) \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = + \infty \) nên đồ thị hàm số \(y = f\left( x \right)\) có 1 đường tiệm cận đứng là \(x = 1\).
Vậy đồ thị hàm số \(y = f\left( x \right)\) có tất cả 3 đường tiệm cận.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
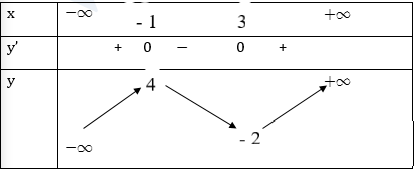
Số đường tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{2019}}{{f\left( x \right)}}\) là:
Quan sát BBT của \(y = f\left( x \right)\), ta thấy, \(f\left( x \right) = 0\) có 3 nghiệm phân biệt \({x_1},\,\,{x_2},\,\,{x_3}\,\,\left( {{x_1} < - 1 < {x_2} < 3 < {x_3}} \right)\)
Xét hàm số \(y = \dfrac{{2019}}{{f\left( x \right)}}\), có: TXĐ \(D = \mathbb{R}\backslash \left\{ {{x_1};{x_2};{x_3}} \right\}\)
Giới hạn của hàm số \(y = \dfrac{{2019}}{{f\left( x \right)}}\) tới các điểm \({x_1};{x_2};{x_3}\) đều là vô cực \( \Rightarrow \) Hàm số \(y = \dfrac{{2019}}{{f\left( x \right)}}\) có 3 TCĐ là: \(x = {x_1},\,\,x = {x_2},\,\,x = {x_3}\).
Cho hàm số \(y = \dfrac{{3x + 1}}{{x - 4}}\) có đồ thị \(\left( C \right)\), với mọi điểm \(M\) thuộc \(\left( C \right)\) thì tích các khoảng cách từ \(M\) tới 2 đường tiệm cận của \(\left( C \right)\) bằng:
Đồ thị hàm số \(y = \dfrac{{3x + 1}}{{x - 4}}\) (C) có TCĐ là: \(x = 4\), TCN là: \(y = 3\)
Lấy điểm \(M\) bất kì thuộc (C), giả sử \(M\left( {{x_0};\dfrac{{3{x_0} + 1}}{{{x_0} - 4}}} \right)\,\,\left( {{x_0} \ne 4} \right)\). Tích khoảng cách từ M tới 2 đường tiệm cận là:
\(\left| {{x_0} - 4} \right|.\left| {\dfrac{{3{x_0} + 1}}{{{x_0} - 4}} - 3} \right| = \left| {{x_0} - 4} \right|.\left| {\dfrac{{13}}{{{x_0} - 4}}} \right| = 13\)
Cho hàm số \(y = \dfrac{{20 + \sqrt {6x - {x^2}} }}{{\sqrt {{x^2} - 8x + 2m} }}\). Tìm tất cả các giá trị của \(m\) sao cho đồ thị hàm số có đúng hai đường tiệm cận đứng.
ĐKXĐ: \(\left\{ \begin{array}{l}0 \le x \le 6\\{x^2} - 8x + 2m > 0\end{array} \right.\)
Để đồ thị hàm số \(y = \dfrac{{20 + \sqrt {6x - {x^2}} }}{{\sqrt {{x^2} - 8x + 2m} }}\) có hai đường tiệm cận đứng thì phương trình \({x^2} - 8x + 2m = 0\) có hai nghiệm phân biệt thuộc đoạn \(\left[ {0;6} \right]\) \( \Leftrightarrow \) Phương trình \({x^2} - 8x = - 2m\) có hai nghiệm phân biệt thuộc đoạn \(\left[ {0;6} \right]\)(*). Xét hàm số \(f\left( x \right) = {x^2} - 8x\) ta có: \(f'\left( x \right) = 2x - 8 = 0 \Leftrightarrow x = 4.\)
Bảng biến thiên:
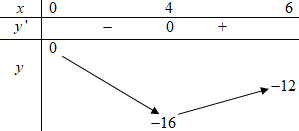
Dựa vào bảng biến thiên ta thì \(\left( * \right) \Leftrightarrow - 16 < - 2m \le - 12 \Leftrightarrow 6 \le m < 8.\)
Vậy \(m \in \left[ {6;8} \right)\).
Gọi \(S\) là tập hợp tất cả các giá trị của tham số \(m\) để đồ thị hàm số \(y = \dfrac{{x - 1}}{{{x^2} + 2mx - m + 2}}\) có đúng hai đường tiệm cận. Tổng tất cả các phần tử của tập \(S\) bằng:
Ta có: \(\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{x - 1}}{{{x^2} + 2mx - m + 2}} = 0\).
Do đó, đồ thị hàm số đã cho luôn nhận đường thẳng \(y = 0\) là tiệm cận ngang với mọi giá trị của \(m\).
Đồ thị hàm số có đúng hai đường tiệm cận khi và chỉ khi nó có đúng 1 đường tiệm cận đứng.
Đồ thị hàm số có đúng 1 tiệm cận đứng khi và chỉ khi phương trình \({x^2} + 2mx - m + 2 = 0\) hoặc có nghiệm kép, hoặc có 2 nghiệm phân biệt trong đó có 1 nghiệm bằng \(1\). (1)
Phương trình \({x^2} + 2mx - m + 2 = 0\) có \(\Delta ' = {m^2} - \left( { - m + 2} \right) = {m^2} + m - 2\)
\(\left( 1 \right) \Leftrightarrow \left[ \begin{array}{l}\Delta ' = 0\\\left\{ \begin{array}{l}\Delta ' > 0\\{1^2} + 2m.1 - m + 2 = 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{m^2} + m - 2 = 0\\\left\{ \begin{array}{l}{m^2} + m - 2 > 0\\3 + m = 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left[ \begin{array}{l}m = 1\\m = - 2\end{array} \right.\\\left\{ \begin{array}{l}m > 1\\m < - 2\\m = - 3\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 2\\m = - 3\end{array} \right.\)
Do đó, tập các giá trị của tham số \(m\) thỏa mãn là \(S = \left\{ {1; - 2; - 3} \right\}\).
Vậy tổng tất cả các phần tử của tập hợp \(S\) bằng \(1 - 2 - 3 = - 4\).

