Câu hỏi:
2 năm trước
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
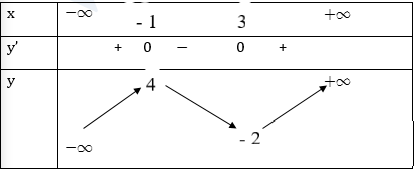
Số đường tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{2019}}{{f\left( x \right)}}\) là:
Trả lời bởi giáo viên
Đáp án đúng: d
Quan sát BBT của \(y = f\left( x \right)\), ta thấy, \(f\left( x \right) = 0\) có 3 nghiệm phân biệt \({x_1},\,\,{x_2},\,\,{x_3}\,\,\left( {{x_1} < - 1 < {x_2} < 3 < {x_3}} \right)\)
Xét hàm số \(y = \dfrac{{2019}}{{f\left( x \right)}}\), có: TXĐ \(D = \mathbb{R}\backslash \left\{ {{x_1};{x_2};{x_3}} \right\}\)
Giới hạn của hàm số \(y = \dfrac{{2019}}{{f\left( x \right)}}\) tới các điểm \({x_1};{x_2};{x_3}\) đều là vô cực \( \Rightarrow \) Hàm số \(y = \dfrac{{2019}}{{f\left( x \right)}}\) có 3 TCĐ là: \(x = {x_1},\,\,x = {x_2},\,\,x = {x_3}\).
Hướng dẫn giải:
Định nghĩa tiệm cận đứng của đồ thị hàm số \(y = f(x)\).
Nếu \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = + \infty \,\)hoặc \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = - \infty \,\)hoặc \(\mathop {\lim }\limits_{x \to {a^ - }} f(x) = + \infty \,\)hoặc \(\mathop {\lim }\limits_{x \to {a^ - }} f(x) = - \infty \,\)thì \(x = a\) là TCĐ của đồ thị hàm số.
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
