Đồ thị hàm số nào sau đây có 3 đường tiệm cận?
Đồ thị hàm số \(y = \dfrac{1}{{{x^2} - 1}}\) có 3 đường tiệm cận là: \(x = 1,\,\,x = - 1,\,\,y = 0\).
Đề thi THPT QG - 2021 - mã 101
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{2x - 1}}{{x - 1}}\) là đường thẳng có phương trình:
Đồ thị hàm số \(y = \dfrac{{2x - 1}}{{x - 1}}\) có TCĐ \(x = 1\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
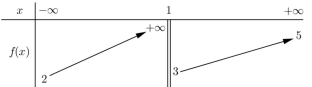
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:
Dựa vào bảng biến thiên ta có:
+) Đồ thị hàm số có 1 tiệm cận đứng là: \(x = 1.\)
+) Đồ thị hàm số có 2 tiệm cận ngang là: \(y = 2,\;y = 5.\)
Vậy đồ thị hàm số có 3 đường tiệm cận.
Tổng số các đường tiệm cận của đồ thị hàm số \(y = \dfrac{{x - 3}}{{\sqrt {{x^2} - 9} }}\) là
ĐK: \({x^2} - 9 > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x > 3}\\{x < - 3}\end{array}} \right.\)
\(\mathop {\lim }\limits_{x \to + \infty } \dfrac{{x - 3}}{{\sqrt {{x^2} - 9} }} = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{1 - \dfrac{3}{x}}}{{\sqrt {1 - \dfrac{9}{{{x^2}}}} }} = 1\)
\( \Rightarrow \) Đồ thị hàm số số có tiệm cận ngang \(y = 1\).
\(\mathop {\lim }\limits_{x \to - \infty } \dfrac{{x - 3}}{{\sqrt {{x^2} - 9} }} = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{1 - \dfrac{3}{x}}}{{\sqrt {1 - \dfrac{9}{{{x^2}}}} }} = - 1\)
\( \Rightarrow \) Đồ thị hàm số có tiệm cận ngang \(y = - 1\).
\(\mathop {\lim }\limits_{x \to + 3} \dfrac{{x - 3}}{{\sqrt {{x^2} - 9} }} = \mathop {\lim }\limits_{x \to + 3} \dfrac{{x - 3}}{{\sqrt {(x - 3)(x + 3)} }}\) \( = \mathop {\lim }\limits_{x \to + 3} \dfrac{{\sqrt {x - 3} }}{{\sqrt {x + 3} }} = \dfrac{{\sqrt {3 - 3} }}{{\sqrt {3 + 3} }} = 0\)
\(\mathop {\lim }\limits_{x \to - 3} \dfrac{{x - 3}}{{\sqrt {{x^2} - 9} }} \ge - \infty \) (Giới hạn dạng \(\dfrac{a}{0}\) với \(a = - 3 - 3 = - 6 < 0\) )
\( \Rightarrow \) Đồ thị hàm số có tiệm cận đứng \(x = - 3\).
Vậy tổng số đường tiệm cận ngang và đường tiệm cận đứng là 3.
Đồ thị hàm số \(y = \dfrac{{{{\left( {x - 1} \right)}^{\dfrac{1}{3}}}}}{{{x^2} + 3x + 2}}\) có bao nhiêu đường tiệm cận?
Điều kiện xác định:\(x \ne - 1;x \ne - 2\).
Ta có: \(\mathop {\lim }\limits_{x \to - {1^ - }} \dfrac{{\sqrt[3]{{x - 1}}}}{{\left( {x + 2} \right)}} = - \sqrt[3]{2} < 0\);\(\mathop {\lim }\limits_{x \to - {1^ - }} \left( {x + 1} \right) = 0\) và
\(\left( {x + 1} \right) < 0\forall x \in \left( { - \infty ; - 1} \right)\)
\( \Rightarrow \mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \dfrac{{\sqrt[3]{{x - 1}}}}{{\left( {x + 1} \right)\left( {x + 2} \right)}} = + \infty \)
\( \Rightarrow \) Hàm số có đường tiệm cận đứng là: \(x = - 1\).
\(\mathop {\lim }\limits_{x \to - {2^ - }} \dfrac{{\sqrt[3]{{x - 1}}}}{{\left( {x + 1} \right)}} = \sqrt[3]{3} > 0\);\(\mathop {\lim }\limits_{x \to - {2^ - }} \left( {x + 2} \right) = 0\) và
\(\left( {x + 2} \right) < 0\forall x \in \left( { - \infty ; - 2} \right)\)
\( \Rightarrow \mathop {\lim }\limits_{x \to - {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {2^ - }} \dfrac{{\sqrt[3]{{x - 1}}}}{{\left( {x + 2} \right)\left( {x + 1} \right)}} = - \infty \)
\( \Rightarrow \) Hàm số có đường tiệm cận đứng là: \(x = - 2\).
Ta có: \(\mathop {\lim }\limits_{x \to \pm \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{\sqrt[3]{{x - 1}}}}{{{x^2} + 3x + 2}} = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{\sqrt[3]{{\dfrac{x}{{{x^6}}} - \dfrac{1}{{{x^6}}}}}}}{{1 + \dfrac{3}{x} + \dfrac{2}{{{x^2}}}}} = 0\)
\( \Rightarrow \)Hàm số có đường tiệm cận ngang là: \(y = 0\)
Vậy hàm số đã cho có 3 đường tiệm cận.
Nếu $\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty $ thì đường thẳng $x = {x_0}$ là:
Nếu $\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty $ thì đường thẳng $x = {x_0}$ là tiệm cận đứng của đồ thị hàm số.
Đồ thị hàm số \(y = \dfrac{{x + \sqrt {{x^2} + 1} }}{{x - 1}}\) có bao nhiêu đường tiệm cận?
Điều kiện: \(x \ne 1.\)
\( \Rightarrow x = 1\) là đường TCĐ của đồ thị hàm số.
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \dfrac{{x + \sqrt {{x^2} + 1} }}{{x - 1}} = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{1 + \sqrt {1 + \dfrac{1}{{{x^2}}}} }}{{1 - \dfrac{1}{x}}} = 2\)
\( \Rightarrow y = 2\) là 1 đường TCN của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to - \infty } \dfrac{{x + \sqrt {{x^2} + 1} }}{{x - 1}} = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{1 - \sqrt {1 + \dfrac{1}{{{x^2}}}} }}{{1 - \dfrac{1}{x}}} = 0\)
\( \Rightarrow y = 0\) là 1 đường TCN của đồ thị hàm số.
Vậy đồ thị hám số đã cho có 2 TCN và 1 TCĐ.
Tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{2x - 1}}{{3x + 5}}\) là đường thẳng
Tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{2x - 1}}{{3x + 5}}\) là đường thẳng \(y = \dfrac{2}{3}\).
Đề thi THPT QG - 2021 - mã 102
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\) là đường thẳng có phương trình
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\) là đường thẳng có phương trình \(x = 2\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ
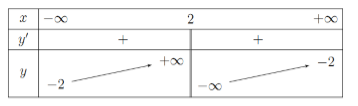
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: \(x = 2,\,\,y = - 2\).
Đề thi THPT QG 2020 – mã đề 104
Tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{3x + 1}}{{x - 1}}\) là:
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{3x + 1}}{{x - 1}} = 3\) và \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{3x + 1}}{{x - 1}} = 3\) nên \(y = 3\) là tiệm cận ngang của đồ thị hàm số.
Phương trình tiệm cận đứng của đồ thị hàm số có dạng:
Phương trình đường tiệm cận đứng có dạng \(x = {x_0}\).
Nếu \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) thì đường thẳng \(y = ax + b\) được gọi là:
Nếu \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) thì đường thẳng \(y = ax + b\) được gọi là tiệm cận xiên của đồ thị hàm số.
Tìm tiệm cận ngang của đồ thị hàm số $y = \dfrac{{1 - x}}{{x + 2}}.$
Ta có $\mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } y = \mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } \dfrac{{1 - x}}{{x + 2}} $ $= \mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } \dfrac{{\dfrac{1}{x} - 1}}{{1 + \dfrac{2}{x}}} = {\rm{\;}} - 1.$
Do đó $y = {\rm{\;}} - 1$ là tiệm cận ngang của đồ thị hàm số.
Cho hàm số \(y = f\left( x \right)\) liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau. Chọn khẳng định đúng?
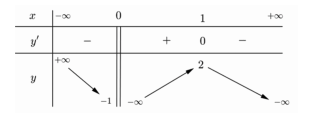
Quan sát bảng biến thiên ta thấy:
\(\mathop {\lim }\limits_{x \to {0^ + }} y = - \infty \) nên \(x = 0\) là TCĐ của đồ thị hàm số.
Ngoài ra \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty ,\mathop {\lim }\limits_{x \to - \infty } y = + \infty \) nên đồ thị hàm số không có tiệm cận ngang.
Vậy đồ thị hàm số chỉ có một đường tiệm cận đứng và không có tiệm cận ngang.
Tiệm cận ngang của đồ thị hàm số:
Phương trình đường tiệm cận ngang có dạng \(y = {y_0}\) nên nó vuông góc với đường thẳng \(x = 0\), hay vuông góc trục tung.
Chọn kết luận đúng:
Đường tiệm cận ngang vẫn có thể cắt đồ thị hàm số, nó chỉ cần thỏa mãn điều kiện \(\mathop {\lim }\limits_{x \to \infty } y = {y_0}\) là được nên các đáp án A, B, D đều sai.
Cho hàm số \(y = f\left( x \right)\) có\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 1;\,\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 1.\) Khẳng định nào sau đây là khẳng định đúng?
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 1 \Rightarrow y = 1\) là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 1 \Rightarrow y = - 1\) là tiệm cận ngang của đồ thị hàm số
Cho hàm số $y = \dfrac{{ax + 1}}{{bx - 2}}.$ Xác định $a$ và $b$ để đồ thị hàm số nhận đường thẳng $x = 1$ là tiệm cận đứng và đường thẳng $y = \dfrac{1}{2}$ là tiệm cận ngang.
Đồ thị hàm số $y = \dfrac{{ax + 1}}{{bx - 2}}$ có hai đường tiệm cận là $y = \dfrac{a}{b}$ (TCN) và $x = \dfrac{2}{b}$ (TCĐ).
Yêu cầu bài toán tương đương với $\dfrac{2}{b} = 1;{\mkern 1mu} {\mkern 1mu} \dfrac{a}{b} = \dfrac{1}{2} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 2}\end{array}} \right..$
Đồ thị hàm số $y = \dfrac{2}{{x - 1}}$ có bao nhiêu đường tiệm cận?
TXĐ: $D = R\backslash \left\{ 1 \right\}$
Ta có: $\mathop {\lim }\limits_{x \to + \infty } {\mkern 1mu} y = \mathop {\lim }\limits_{x \to - \infty } {\mkern 1mu} y = 0 \Rightarrow y = 0$ là TCN của đồ thị hàm số.
$\mathop {\lim }\limits_{x \to {1^ + }} {\mkern 1mu} y = + \infty ;{\mkern 1mu} {\mkern 1mu} \mathop {\lim }\limits_{x \to {1^ - }} {\mkern 1mu} y = - \infty \Rightarrow x = 1$ là TCĐ của đồ thị hàm số.
Vậy đồ thị hàm số $y = \dfrac{2}{{x - 1}}$ có 2 đường tiệm cận.

