Đường tiệm cận của đồ thị hàm số và luyện tập

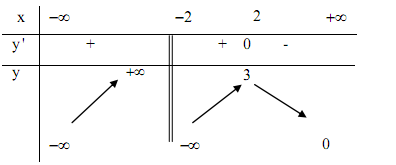
Vì \(\mathop {\lim }\limits_{x \to  - {2^ + }} y =  - \infty \) nên \(x =  - 2\) là tiệm cận đứng của đồ thị hàm số.

Vì \(\mathop {\lim }\limits_{x \to  + \infty } y = 0\) nên \(y = 0\) là tiệm cận ngang của đồ thị hàm số.

Hàm đa thức không có đường tiệm cận nên D đúng.

Ngoài ra dễ dàng tìm được đường tiệm cận của mỗi đáp án A, B, C.

Đáp án A: Tiệm cận ngang \(y =  \pm 1\), không có tiệm cận đứng.

Đáp án B: Tiệm cận đứng \(x =  \pm 1\), tiệm cận ngang \(y = 0\).

Đáp án C: Tiệm cận ngang \(y = \dfrac{3}{4}\), tiệm cận đứng \(x = \dfrac{3}{4}\).

Ta có $y = \dfrac{{\sqrt {5 + x}  - 1}}{{{x^2} + 4x}} $ $= \dfrac{{\sqrt {5 + x}  - 1}}{{x\left( {x + 4} \right)}} $ $ = \dfrac{{\left( {\sqrt {5 + x} - 1} \right)\left( {\sqrt {5 + x} + 1} \right)}}{{x\left( {x + 4} \right)\left( {\sqrt {5 + x} + 1} \right)}}$ $ = \dfrac{{5 + x - 1}}{{x\left( {x + 4} \right)\left( {\sqrt {5 + x} + 1} \right)}} $ $= \dfrac{{x + 4}}{{x\left( {x + 4} \right)\left( {\sqrt {5 + x} + 1} \right)}}$ $= \dfrac{1}{{x\left( {\sqrt {5 + x}  + 1} \right)}}.$

Vì $\mathop {\lim }\limits_{x \to {0^+ }} y = + \infty $ nên $x = 0$ là tiệm cận đứng của ĐTHS.

$\mathop {\lim }\limits_{x \to - 4} y = - \frac{1}{8} \Rightarrow x = - 4$ không là TCĐ của ĐTHS.

TXĐ: $D = R{\rm{ }}\backslash {\rm{ }}\left\{ 1 \right\}$. 

Ta có: $\mathop {\lim }\limits_{x \to \infty } {\mkern 1mu} \dfrac{{\sqrt[3]{{ - {x^3} + 3{x^2}}}}}{{x - 1}} = \mathop {\lim }\limits_{x \to \infty } {\mkern 1mu} \dfrac{{\dfrac{{\sqrt[3]{{ - {x^3} + 3{x^2}}}}}{x}}}{{\dfrac{{x - 1}}{x}}} = \mathop {\lim }\limits_{x \to \infty } {\mkern 1mu} \dfrac{{\sqrt[3]{{ - 1 + \dfrac{3}{x}}}}}{{1 - \dfrac{1}{x}}} =  - 1$

$ \Rightarrow y =  - 1$ là tiệm cận ngang của hàm số đã cho.

$\mathop {\lim }\limits_{x \to \infty } y = {\rm{\;}} - 1 \Rightarrow y = {\rm{\;}} - 1$ là tiệm cận ngang của đồ thị hàm số.

Ta có: ${x^2} - x + 2 = 0 \Leftrightarrow {\left( {x - \dfrac{1}{2}} \right)^2} + \dfrac{7}{4} = 0 \Rightarrow $ phương trình vô nghiệm. Hàm số không có TCĐ.

Xét ${x^2} + 1 = 0$ vô nghiệm $ \Rightarrow $ Hàm số không có TCĐ.

Xét hàm số  ta có: $\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{2}{{\sqrt x }} = {\rm{\;}} + \infty {\rm{\;}} \Rightarrow x = 0$ là tiệm cận đứng của đồ thị hàm số.

Xét ${x^4} + 1 = 0$ vô nghiệm $ \Rightarrow $ Hàm số không có TCĐ.

Đồ thị hàm số \(y = \dfrac{{2x - 3}}{{x + 1}}\) có 2 tiệm cận là \(x =  - 1,\,\,y = 2.\)

Hình phẳng được giới hạn bởi các đường tiệm cận và hai trục tọa độ là hình chữ nhật có chiều rộng là 1, chiều dài là 2. Diện tích hình phẳng đó là: 1.2 = 2.

Ta thấy mẫu thức ${x^2} - 1$ có 2 nghiệm $x =  \pm 1$

x=1 không là nghiệm của tử nên x=1 là 1 TCĐ.

Ta có:

$\begin{array}{l}
\mathop {\lim }\limits_{x \to - 1} y = \mathop {\lim }\limits_{x \to - 1} \frac{{\sqrt {{x^2} - x + 2} - 2}}{{{x^2} - 1}}\\
= \mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} - x + 2 - 4}}{{\left( {{x^2} - 1} \right)\left( {\sqrt {{x^2} - x + 2} + 2} \right)}}\\
= \mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} - x - 2}}{{\left( {{x^2} - 1} \right)\left( {\sqrt {{x^2} - x + 2} + 2} \right)}}\\
= \mathop {\lim }\limits_{x \to - 1} \frac{{\left( {x + 1} \right)\left( {x - 2} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)\left( {\sqrt {{x^2} - x + 2} + 2} \right)}}\\
= \mathop {\lim }\limits_{x \to - 1} \frac{{x - 2}}{{\left( {x - 1} \right)\left( {\sqrt {{x^2} - x + 2} + 2} \right)}} = \frac{3}{8}
\end{array}$

Do đó x=-1 không là đường tiệm cận của đths.

Vậy ĐTHS có 1 đường TCĐ.

$y = \dfrac{{x + 1}}{{{x^2} + 6x - 7}} = \dfrac{{x + 1}}{{\left( {x - 1} \right)\left( {x + 7} \right)}}$  (TXĐ: $D = R\backslash \left\{ { - 7,1} \right\}$)

Ta có $\mathop {\lim }\limits_{x \to \infty } {\mkern 1mu} y = 0 \Rightarrow TCN{\mkern 1mu} y = 0$$\mathop {\lim }\limits_{x \to 1} {\mkern 1mu} y = \infty  \Rightarrow $TCĐ $x = 1$$\mathop {\lim }\limits_{x \to  - 7} {\mkern 1mu} y = \infty  \Rightarrow $TCĐ $x =  - 7$

Vậy số đường tiệm cận của đồ thi hàm số là ba, nên ta chọn Đáp án D.

Ta có: $\mathop {\lim }\limits_{x \to  + \infty } {\mkern 1mu} y = \mathop {\lim }\limits_{x \to  + \infty } {\mkern 1mu} \dfrac{{2x + 2017}}{{x + 1}} = \mathop {\lim }\limits_{x \to  + \infty } {\mkern 1mu} \dfrac{{2 + \dfrac{{2017}}{x}}}{{1 + \dfrac{1}{x}}} = 2 \Rightarrow y = 2$ là TCN

$\mathop {\lim }\limits_{x \to  - \infty } {\mkern 1mu} y = \mathop {\lim }\limits_{x \to  - \infty } {\mkern 1mu} \dfrac{{2x + 2017}}{{ - x + 1}} = \mathop {\lim }\limits_{x \to  + \infty } {\mkern 1mu} \dfrac{{2 + \dfrac{{2017}}{x}}}{{ - 1 + \dfrac{1}{x}}} = 2 \Rightarrow y =  - 2$ là TCN.

Vậy đồ thị hàm số có $2$ tiệm cận ngang là các đường thẳng $y =  - 2;y = 2$.

Đồ thị hàm số có tiệm cận đứng $x =  - m{\mkern 1mu} {\mkern 1mu} \left( d \right),M \in d \Rightarrow 2 =  - m \Rightarrow m =  - 2.$

Ta có: \(\mathop {\lim }\limits_{x \to  + \infty } \dfrac{{f\left( x \right)}}{x} = \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{\sqrt {{x^4} - 3{x^2} + 5} }}{{x\left( {x - 2} \right)}} \) \(= \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{\sqrt {1 - \dfrac{3}{{{x^2}}} + \dfrac{5}{{{x^4}}}} }}{{1 - \dfrac{2}{x}}} = 1 = \mathop {\lim }\limits_{x \to  - \infty } \dfrac{{f\left( x \right)}}{x} \) \(\Rightarrow a = 1\) .

\(\begin{array}{l}\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - x} \right] = \mathop {\lim }\limits_{x \to  + \infty } \left[ {\dfrac{{\sqrt {{x^4} - 3{x^2} + 5} }}{{x - 2}} - x} \right] \\= \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{\sqrt {{x^4} - 3{x^2} + 5}  - \left( {{x^2} - 2x} \right)}}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{4{x^3} - 7{x^2} + 5}}{{\left( {x - 2} \right)\left[ {\sqrt {{x^4} - 3{x^2} + 5}  + \left( {{x^2} - 2x} \right)} \right]}} \\= \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{4 - \dfrac{7}{x} + \dfrac{5}{{{x^3}}}}}{{\left( {1 - \dfrac{2}{x}} \right)\left( {\sqrt {1 - \dfrac{3}{{{x^2}}} + \dfrac{5}{{{x^4}}}}  + 1 - \dfrac{2}{x}} \right)}} = \dfrac{4}{2} = 2\\\mathop {\lim }\limits_{x \to  - \infty } \left[ {f\left( x \right) - x} \right] = 2 \Rightarrow b = 2\end{array}\)

Vậy tiệm cận xiên của đồ thị hàm số là \(y = x + 2\).

Hàm số có dạng $y = \dfrac{{f\left( x \right)}}{{g\left( x \right)}}$ với $f\left( x \right) = 5x + 1 - \sqrt {x + 1} ;{\mkern 1mu} {\mkern 1mu} g\left( x \right) = {x^2} - 2x$

*) Do bậc của $f\left( x \right)$ nhỏ hơn bậc của $g\left( x \right)$ $ \Rightarrow $ TCN :$y = 0$

*) Do : $g\left( x \right) = 0 \Leftrightarrow {x^2} - 2x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2}\\{x = 0}\end{array}} \right.$ và $f\left( 2 \right) \ne 0 \Rightarrow \mathop {\lim }\limits_{x \to 2} {\mkern 1mu} \dfrac{{f\left( x \right)}}{{g\left( x \right)}} = \infty  \Rightarrow $ TCĐ :$x = 2$

*) Do $f\left( 0 \right) = 0$ nên kiểm tra:

$\mathop {\lim }\limits_{x \to 0} \dfrac{{f\left( x \right)}}{{g\left( x \right)}} $ $= \mathop {\lim }\limits_{x \to 0} {\mkern 1mu} \dfrac{{{{\left( {5x + 1} \right)}^2} - \left( {x + 1} \right)}}{{x\left( {x - 2} \right)\left( {5x + 1 + \sqrt {x + 1} } \right)}} $ $= \mathop {\lim }\limits_{x \to 0} \dfrac{{25x + 9}}{{\left( {x - 2} \right)\left( {5x + 1 + \sqrt {x + 1} } \right)}} =  - \dfrac{9}{4} \ne \infty $

(Lưu ý: có thể kiểm tra bằng máy tính)

Do đó đồ thị hàm số có hai đường tiệm cận là $y = 0$ và $x = 2$.

Đồ thị hàm số $\left( C \right)$ có TCĐ$x = 3{\mkern 1mu} {\mkern 1mu} \left( {{d_1}} \right)$ và TCN:$y = 3{\mkern 1mu} {\mkern 1mu} \left( {{d_2}} \right)$

$ \Rightarrow $ Tâm đối xứng của đồ thị$\left( C \right)$ là:$I\left( {3;3} \right)$

Gọi$M\left( {m;\dfrac{{1 - 3m}}{{3 - m}}} \right) \in \left( C \right)$ ta có:$d\left( {M;{d_1}} \right) = \left| {m - 3} \right|;{\mkern 1mu} {\mkern 1mu} d\left( {M;\left( {{d_2}} \right)} \right) = \left| {\dfrac{{1 - 3m}}{{3 - m}} - 3} \right| = \dfrac{8}{{\left| {3 - m} \right|}}$

Vì$d\left( {M;\left( {{d_1}} \right)} \right) = 2d\left( {M;\left( {{d_2}} \right)} \right) \Rightarrow \left| {m - 3} \right| = \dfrac{{16}}{{\left| {3 - m} \right|}} \Leftrightarrow {\left( {m - 3} \right)^2} = 16 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 7}\\{m =  - 1}\end{array}} \right.$

Khi$m = 7 \Rightarrow M\left( {7;5} \right) \Rightarrow IM = \sqrt {{{\left( {7 - 3} \right)}^2} + {{\left( {5 - 3} \right)}^2}}  = 2\sqrt 5 $

Khi$m =  - 1 \Rightarrow M\left( { - 1;1} \right) \Rightarrow IM = \sqrt {{{\left( { - 1 - 3} \right)}^2} + {{\left( {1 - 3} \right)}^2}}  = 2\sqrt 5 $

Chọn $m = 2,$ khi đó hàm số trở thành $y = \dfrac{{1 + \sqrt {x + 1} }}{{\sqrt {{x^2} - 2x - 6} }}$

Rõ ràng $1 + \sqrt {x + 1}  > 0{\mkern 1mu} ,\forall x \ge  - 1$

Khi đó để hàm số$y = \dfrac{{1 + \sqrt {x + 1} }}{{\sqrt {{x^2} - mx - 3m} }}$ có hai tiệm cận đứng thì phương trình ${x^2} - mx - 3m = 0$ cần có hai nghiệm phân biệt thuộc $\left[ { - 1; + \infty } \right)$ .

Gọi hai nghiệm phân biệt là \({x_1}\) và \({x_2}\).

Khi đó ta phải có

\(\left\{ {\begin{array}{*{20}{l}}{\Delta  > 0}\\{{x_1},{x_2} \ge  - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{{\left( { - m} \right)}^2} - 4\left( { - 3m} \right) > 0}\\{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) \ge 0}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} + 12m > 0}\\{{x_1}{x_2} + {x_1} + {x_2} + 1 \ge 0}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \in \left( { - \infty ; - 12} \right) \cup \left( {0; + \infty } \right)}\\{-3m + m + 1 \ge 0}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \in \left( { - \infty ; - 12} \right) \cup \left( {0; + \infty } \right)}\\{m \le  \dfrac{1}{2}}\end{array}} \right.\) \( \Leftrightarrow m \in \left( {0; \dfrac{1}{2} } \right]\)

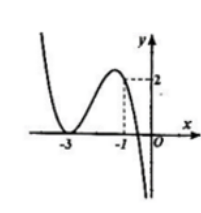
Ta có $y = \dfrac{{\left( {{x^2} + 4x + 3} \right)\sqrt {{x^2} + x} }}{{x\left[ {{f^2}\left( x \right) - 2f\left( x \right)} \right]}} = \dfrac{{\left( {x + 1} \right)\left( {x + 3} \right)\sqrt {{x^2} + x} }}{{x.f\left( x \right)\left[ {f\left( x \right) - 2} \right]}}$

ĐK: $\left\{ {\begin{array}{*{20}{l}}{x\left( {x + 1} \right) \ge 0}\\{x \ne 0}\\{f\left( x \right) \ne 0}\\{f\left( x \right) \ne 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \in \left( { - \infty ; - 1} \right] \cup \left( {0; + \infty } \right)}\\{f\left( x \right) \ne 0}\\{f\left( x \right) \ne 2}\end{array}} \right.$ .

Dựa vào đồ thị hàm số ta thấy phương trình $f\left( x \right) = 0$ có nghiệm kép $x =  - 3$ và $1$ nghiệm $x = a \in \left( { - 1;0} \right)$ , khi đó $f\left( x \right) = m{\left( {x + 3} \right)^2}\left( {x - a} \right){\mkern 1mu} {\mkern 1mu} \left( {m \ne 0} \right)$ .

Xét phương trình $f\left( x \right) - 2 = 0 \Leftrightarrow f\left( x \right) = 2,$ phương trình có $3$ nghiệm phân biệt$x =  - 1;{\mkern 1mu} {\mkern 1mu} x = b \in \left( { - 3; - 1} \right);{\mkern 1mu} {\mkern 1mu} x = c \in \left( { - \infty ; - 3} \right)$ , khi đó $f\left( x \right) - 2 = n\left( {x + 1} \right)\left( {x - b} \right)\left( {x - c} \right)$ .

Khi đó điều kiện xác định là :$\left\{ \begin{array}{l}{\rm{\;}}x \in \left( { - \infty ; - 1} \right) \cup \left( {0; + \infty {\rm{\;}}} \right)\\{\rm{ \;}}x \ne  - 3\\{\rm{ \;}}x \ne b;{\mkern 1mu} {\mkern 1mu} x \ne c\end{array} \right.$

$ \Rightarrow y = \dfrac{{\left( {x + 1} \right)\left( {x + 3} \right)\sqrt {{x^2} + x} }}{{x.m{{\left( {x + 3} \right)}^2}\left( {x - a} \right).n\left( {x + 1} \right)\left( {x - b} \right)\left( {x - c} \right)}} = \dfrac{{\left( {x + 1} \right)\sqrt {{x^2} + x} }}{{mn.x\left( {x + 3} \right)\left( {x - a} \right)\left( {x - b} \right)\left( {x - c} \right)}}$

Khi $x = a \in \left( {-1;0} \right)$ $ \Rightarrow $ Hàm số không xác định.

Vây đồ thị hàm số có $4$ TCĐ là $x = 0;{\mkern 1mu} {\mkern 1mu} x =  - 3;{\mkern 1mu} {\mkern 1mu} x = b;{\mkern 1mu} {\mkern 1mu} x = c$

Ta có: $\mathop {\lim }\limits_{x \to {\rm{\;}} - {1^ + }} y = {\rm{\;}} - \infty $. Suy ra : $x = {\rm{\;}} - 1$ là tiệm cận đứng của đồ thị hàm số

Và $\mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } y = 2$. Suy ra $y = 2$ là tiệm cận ngang của đồ thị hàm số.

Ta có \(\mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \dfrac{{x - m}}{{{x^2} - 3x + 2}} \) \(= \mathop {\lim }\limits_{x \to \infty } \dfrac{{\dfrac{1}{x} - \dfrac{m}{{{x^2}}}}}{{1 - \dfrac{3}{x} + \dfrac{2}{{{x^2}}}}} = 0 \)

\(\Rightarrow y = 0\) là TCN của đồ thị hàm số.

Ta có \({x^2} - 3x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right. \) \(\Rightarrow y = \dfrac{{x - m}}{{{x^2} - 3x + 2}} = \dfrac{{x - m}}{{\left( {x - 1} \right)\left( {x - 2} \right)}}\)

Để đồ thị hàm số \(y = \dfrac{{x - m}}{{{x^2} - 3x + 2}}\) có đúng hai tiệm cận thì đồ thị hàm số chỉ có 1 TCN \( \Rightarrow \left[ \begin{array}{l}m = 1\\m = 2\end{array} \right.\)

Đồ thị hàm số có TCN là \(y =  - \dfrac{1}{3}\).

Đường thẳng $y = {y_0}$ là tiệm cận ngang của đồ thị hàm số $y = f\left( x \right)$ nếu $\left[ \begin{gathered}  \mathop {\lim }\limits_{x \to  + \infty } y = {y_0} \hfill \\ \mathop {\lim }\limits_{x \to  - \infty } y = {y_0} \hfill \\ \end{gathered}  \right.$