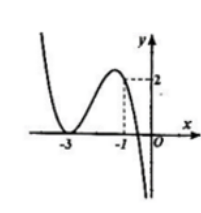
Cho đồ thị hàm bậc ba$y = f\left( x \right)$ như hình vẽ. Hỏi đồ thị hàm số $y = \dfrac{{\left( {{x^2} + 4x + 3} \right)\sqrt {{x^2} + x} }}{{x\left[ {{f^2}\left( x \right) - 2f\left( x \right)} \right]}}$ có bao nhiêu đường tiệm cận đứng?

Ta có $y = \dfrac{{\left( {{x^2} + 4x + 3} \right)\sqrt {{x^2} + x} }}{{x\left[ {{f^2}\left( x \right) - 2f\left( x \right)} \right]}} = \dfrac{{\left( {x + 1} \right)\left( {x + 3} \right)\sqrt {{x^2} + x} }}{{x.f\left( x \right)\left[ {f\left( x \right) - 2} \right]}}$

ĐK: $\left\{ {\begin{array}{*{20}{l}}{x\left( {x + 1} \right) \ge 0}\\{x \ne 0}\\{f\left( x \right) \ne 0}\\{f\left( x \right) \ne 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \in \left( { - \infty ; - 1} \right] \cup \left( {0; + \infty } \right)}\\{f\left( x \right) \ne 0}\\{f\left( x \right) \ne 2}\end{array}} \right.$ .

Dựa vào đồ thị hàm số ta thấy phương trình $f\left( x \right) = 0$ có nghiệm kép $x =  - 3$ và $1$ nghiệm $x = a \in \left( { - 1;0} \right)$ , khi đó $f\left( x \right) = m{\left( {x + 3} \right)^2}\left( {x - a} \right){\mkern 1mu} {\mkern 1mu} \left( {m \ne 0} \right)$ .

Xét phương trình $f\left( x \right) - 2 = 0 \Leftrightarrow f\left( x \right) = 2,$ phương trình có $3$ nghiệm phân biệt$x =  - 1;{\mkern 1mu} {\mkern 1mu} x = b \in \left( { - 3; - 1} \right);{\mkern 1mu} {\mkern 1mu} x = c \in \left( { - \infty ; - 3} \right)$ , khi đó $f\left( x \right) - 2 = n\left( {x + 1} \right)\left( {x - b} \right)\left( {x - c} \right)$ .

Khi đó điều kiện xác định là :$\left\{ \begin{array}{l}{\rm{\;}}x \in \left( { - \infty ; - 1} \right) \cup \left( {0; + \infty {\rm{\;}}} \right)\\{\rm{ \;}}x \ne  - 3\\{\rm{ \;}}x \ne b;{\mkern 1mu} {\mkern 1mu} x \ne c\end{array} \right.$

$ \Rightarrow y = \dfrac{{\left( {x + 1} \right)\left( {x + 3} \right)\sqrt {{x^2} + x} }}{{x.m{{\left( {x + 3} \right)}^2}\left( {x - a} \right).n\left( {x + 1} \right)\left( {x - b} \right)\left( {x - c} \right)}} = \dfrac{{\left( {x + 1} \right)\sqrt {{x^2} + x} }}{{mn.x\left( {x + 3} \right)\left( {x - a} \right)\left( {x - b} \right)\left( {x - c} \right)}}$

Khi $x = a \in \left( {-1;0} \right)$ $ \Rightarrow $ Hàm số không xác định.

Vây đồ thị hàm số có $4$ TCĐ là $x = 0;{\mkern 1mu} {\mkern 1mu} x =  - 3;{\mkern 1mu} {\mkern 1mu} x = b;{\mkern 1mu} {\mkern 1mu} x = c$