Tổng hợp câu hay và khó chương 2 - Phần 3

$\begin{array}{l}{\log _{\sqrt 3 }}\dfrac{{x + y}}{{{x^2} + {y^2} + xy + 2}} = x\left( {x - 3} \right) + y\left( {y - 3} \right) + xy\,\,\,\,\,\,\left( 1 \right)\\ \Leftrightarrow {\log _{\sqrt 3 }}\left( {x + y} \right) - {\log _{\sqrt 3 }}\left( {{x^2} + {y^2} + xy + 2} \right) = {x^2} - 3x + {y^2} - 3y + xy\\ \Leftrightarrow {\log _{\sqrt 3 }}\left( {x + y} \right) + 3x + 3y = {\log _{\sqrt 3 }}\left( {{x^2} + {y^2} + xy + 2} \right) + {x^2} + {y^2} + xy\\ \Leftrightarrow {\log _{\sqrt 3 }}\left( {x + y} \right) + 2 + 3x + 3y = {\log _{\sqrt 3 }}\left( {{x^2} + {y^2} + xy + 2} \right) + {x^2} + {y^2} + xy + 2\\ \Leftrightarrow {\log _{\sqrt 3 }}\left( {3x + 3y} \right) + 3x + 3y = {\log _{\sqrt 3 }}\left( {{x^2} + {y^2} + xy + 2} \right) + {x^2} + {y^2} + xy + 2\,\,\,\,\,\,\left( 2 \right)\end{array}$

Đặt $f\left( t \right) = {\log _{\sqrt 3 }}t + t\,\,\,\left( {t > 0} \right)$$\Rightarrow f'\left( t \right) = \dfrac{1}{{t\ln \sqrt 3 }} + 1 > 0,\forall t > 0$

$\Rightarrow f\left( t \right)$ đồng biến trên $\left( {0; + \infty } \right)$

$\begin{array}{l}\left( 2 \right) \Leftrightarrow f\left( {3x + 3y} \right) = f\left( {{x^2} + {y^2} + xy + 2} \right) \Leftrightarrow 3x + 3y = {x^2} + {y^2} + xy + 2\\ \Leftrightarrow 4{x^2} + 4{y^2} + 4xy - 12x - 12y + 8 = 0\\ \Leftrightarrow {\left( {2x + y} \right)^2} - 6\left( {2x + y} \right) + 5 =  - 3{\left( {y - 1} \right)^2} \le 0 \Leftrightarrow 1 \le 2x + y \le 5\end{array}$

Khi đó, $P = \dfrac{{5x + 4y + 4}}{{x + y + 3}} = 3 + \dfrac{{2x + y - 5}}{{x + y + 3}} \le 3$, vì $\left\{ \begin{array}{l}2x + y - 5 \le 0\\x + y + 3 > 0\end{array} \right.$

Vậy ${P_{m{\rm{ax}}}} = 3$ khi và chỉ khi $\left\{ \begin{array}{l}2x + y - 5 = 0\\y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.$

Đặt $t = {3^{1 + x}} - {3^{1 - x}} = f\left( x \right),\forall x \in \left[ {0;1} \right]$ ta có $f'\left( x \right) = {3^{1 + x}}\ln 3 + {3^{1 - x}}\ln 3 > 0$

$\Rightarrow$ hàm số đồng biến trên $\left[ {0;1} \right]$, $\Rightarrow f\left( 0 \right) = 0 \le f\left( x \right) \le f\left( 1 \right) = 8 \Rightarrow f\left( x \right) \in \left[ {0;8} \right]$  hay $t \in \left[ {0;8} \right]$ 

Ta có ${t^2} = {9^{1 + x}} + {9^{1 - x}} - {2.3^{1 + x + 1 - x}} = {9^{1 + x}} + {9^{1 - x}} - 18 \Leftrightarrow {9^{1 + x}} + {9^{1 - x}} = {t^2} + 18$

Khi đó phương trình trở thành ${t^2} + 18 = 3\left( {m + 2} \right)t + 45 - 27m$

$\begin{array}{l} \Leftrightarrow {t^2} - 3\left( {m + 2} \right)t + 27m - 27 = 0\,\,\forall t \in \left[ {0;8} \right]\\ \Leftrightarrow {t^2} - 6t - 27 - 3m\left( {t - 9} \right) = 0\\ \Leftrightarrow \left( {t - 9} \right)\left( {t + 3} \right) - 3m\left( {t - 9} \right) = 0\\ \Leftrightarrow \left( {t - 9} \right)\left( {t + 3 - 3m} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t = 9 \notin \left[ {0;8} \right]\\t = 3m - 3\end{array} \right.\end{array}$

Đề phương trình ban đầu có nghiệm $x \in \left[ {0;1} \right]$ thì phương trình (*) có nghiệm $t \in \left[ {0;8} \right]$ thì

$0 \le 3m - 3 \le 8 \Leftrightarrow 1 \le m \le \dfrac{{11}}{3}\mathop  \Leftrightarrow \limits^{m \in Z} m \in \left\{ {1;2;3} \right\}$

Vậy có $3$ giá trị $m$ nguyên để phương trình ban đầu có nghiệm thuộc $[0; 1]$

${\log _{\dfrac{1}{3}}}x + {\log _{\dfrac{1}{3}}}y \le {\log _{\dfrac{1}{3}}}\left( {{x^2} + y} \right) \Leftrightarrow {\log _{\dfrac{1}{3}}}\left( {xy} \right) \le {\log _{\dfrac{1}{3}}}\left( {{x^2} + y} \right) \Leftrightarrow xy \ge {x^2} + y \Leftrightarrow y\left( {x - 1} \right) \ge {x^2}$

Với x = 1 ta có $0 \ge 1$ (Vô lý) $\Rightarrow x \ne 1$ .

Ta có $y\left( {x - 1} \right) = {x^2} \ge 0,$  mà $y > 0 \Rightarrow x - 1 \ge 0 \Leftrightarrow x \ge 1.$  Vậy $x > 1$

Khi đó ta có :

$P = 3x + 2y = \dfrac{{\left( {3x + 2y} \right)\left( {x - 1} \right)}}{{x - 1}} = \dfrac{{3x\left( {x - 1} \right) + 2y\left( {x - 1} \right)}}{{x - 1}} \ge \dfrac{{3{x^2} - 3x + 2{x^2}}}{{x - 1}} = \dfrac{{5{x^2} - 3x}}{{x - 1}} = f\left( x \right)\,\,\,\forall x > 1$

Xét hàm số $f\left( x \right) = \dfrac{{5{x^2} - 3x}}{{x - 1}} = 5x + 2 + \dfrac{2}{{x - 1}}\,\,\,\left( {x > 1} \right)$ ta có

$f'\left( x \right) = 5 - \dfrac{2}{{{{\left( {x - 1} \right)}^2}}} = \dfrac{{5{{\left( {x - 1} \right)}^2} - 2}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 + \dfrac{{\sqrt {10} }}{5}\\x = 1 - \dfrac{{\sqrt {10} }}{5}\end{array} \right.$

BBT :

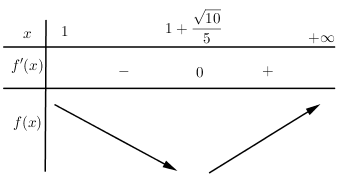
Dựa vào BBT ta thấy

$\begin{array}{l}\mathop {\min }\limits_{\left( {1; + \infty } \right)} f\left( x \right) = f\left( {1 + \dfrac{{\sqrt {10} }}{5}} \right) = 5\left( {1 + \dfrac{{\sqrt {10} }}{5}} \right) + 2 + \dfrac{2}{{1 + \dfrac{{\sqrt {10} }}{5} - 1}} = 5 + \sqrt {10}  + 2 + \sqrt {10}  = 7 + 2\sqrt {10} \\ \Rightarrow P \ge f\left( x \right) \ge 7 + 2\sqrt {10}  \Rightarrow {P_{\min }} = 7 + 2\sqrt {10} \end{array}$

${\left( {3 - \sqrt 5 } \right)^{{x^2}}} + m{\left( {3 + \sqrt 5 } \right)^{{x^2}}} - {2^{{x^2} - 1}} = 0$$\Leftrightarrow {\left( {\dfrac{{3 - \sqrt 5 }}{2}} \right)^{{x^2}}} + m{\left( {\dfrac{{3 + \sqrt 5 }}{2}} \right)^{{x^2}}} - \dfrac{1}{2} = 0$

Ta có ${\left( {\dfrac{{3 - \sqrt 5 }}{2}} \right)^{{x^2}}}.{\left( {\dfrac{{3 + \sqrt 5 }}{2}} \right)^{{x^2}}} = {\left( {\dfrac{{3 - \sqrt 5 }}{2}.\dfrac{{3 + \sqrt 5 }}{2}} \right)^{{x^2}}} = 1$

Đặt ${\left( {\dfrac{{3 - \sqrt 5 }}{2}} \right)^{{x^2}}} = t\,\, \Leftrightarrow {\left( {\dfrac{{3 + \sqrt 5 }}{2}} \right)^{{x^2}}} = \dfrac{1}{t}$$\Rightarrow t = {\left( {\dfrac{2}{{3 + \sqrt 5 }}} \right)^{{x^2}}} \Leftrightarrow {x^2} = {\log _{\frac{2}{{3 + \sqrt 5 }}}}t$, khi đó phương trình trở thành: $t + m\dfrac{1}{t} - \dfrac{1}{2} = 0 \Leftrightarrow {t^2} - \dfrac{1}{2}t + m = 0\,$ $\Leftrightarrow 2{t^2} - t + 2m = 0\,$ $\Leftrightarrow m = \dfrac{{t - 2{t^2}}}{2}$

Phương trình đã cho có hai nghiệm phân biệt $\Leftrightarrow {x^2} > 0 \Leftrightarrow {\log _{\frac{2}{{3 + \sqrt 5 }}}}t > 0 \Leftrightarrow 0 < t < 1.$

(ứng với mỗi nghiệm $t$ thỏa mãn $0<t<1$ thì ta có $2$ nghiệm $x$)

Do đó ta cần tìm $m$ để phương trình ẩn $t$ chỉ có $1$ nghiệm thuộc $(0;1)$.

Xét hàm $f\left( t \right) = \dfrac{{t - 2{t^2}}}{2}$ có $f'\left( t \right) = \dfrac{{1 - 4t}}{2} = 0 \Leftrightarrow t = \dfrac{1}{4}$

Bảng biến thiên:

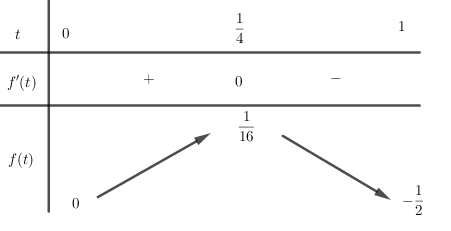
Vậy $- \dfrac{1}{2} < m \le 0$ hoặc $m = \dfrac{1}{{16}}$

Đặt $g(x) = f(x) - 2018 = a.\ln \left( {x + \sqrt {{x^2} + 1} } \right) + b.{x^{2017}}$

$\begin{array}{l} \Rightarrow g( - x) = a.\ln \left( { - x + \sqrt {{x^2} + 1} } \right) - b.{x^{2017}} = a.\ln \left( {\dfrac{1}{{x + \sqrt {{x^2} + 1} }}} \right) - b.{x^{2017}} =  - a.\ln \left( {x + \sqrt {{x^2} + 1} } \right) - b.{x^{2017}} =  - g(x)\\ \Rightarrow f( - x) - 2018 =  - \left( {f(x) - 2018} \right) \Leftrightarrow f( - x) =  - f(x) + 4036\end{array}$

Ta có:

$\begin{array}{l}f\left( {\log \left( {\ln 10} \right)} \right) = f\left( {\log \left( {\dfrac{{\log 10}}{{\log e}}} \right)} \right) = f\left( {\log \left( {\dfrac{1}{{\log e}}} \right)} \right) = f\left( { - \log \left( {\log e} \right)} \right) =  - f\left( {\log \left( {\log e} \right)} \right) + 4036\\ =  - 2019 + 4036 = 2017\end{array}$

Ta có: ${2^{{{(x - 1)}^2}}}.{\log _2}({x^2} - 2x + 3) = {4^{\left| {x - m} \right|}}.{\log _2}\left( {2\left| {x - m} \right| + 2} \right)$

$\Leftrightarrow {2^{{{(x - 1)}^2}}}.{\log _2}({(x - 1)^2} + 2) = {2^{2\left| {x - m} \right|}}.{\log _2}\left( {2\left| {x - m} \right| + 2} \right)$  (1)

Xét hàm số $y = f(t) = {2^t}.{\log _2}(t + 2)$ trên $\left[ {0; + \infty } \right)$:

$f'(t) = {2^t}\ln 2.{\log _2}(t + 2) + {2^t}.\dfrac{1}{{\ln 2.(t + 2)}} > 0,\,\,\forall t \ge 0 \Rightarrow$Hàm số đồng biến trên $\left[ {0; + \infty } \right)$

Phương trình $(1) \Leftrightarrow f\left( {{{(x - 1)}^2}} \right) = f\left( {2\left| {x - m} \right|} \right)$$\Leftrightarrow {(x - 1)^2} = 2\left| {x - m} \right|\,\,\left( 2 \right)$

Thử đáp án:

+) Nếu $m = 1$ thì $\left( 2 \right)$ trở thành ${\left( {x - 1} \right)^2} = 2\left| {x - 1} \right|$

Nếu $x \ge 1$ thì ${\left( {x - 1} \right)^2} = 2\left( {x - 1} \right) \Leftrightarrow \left( {x - 1} \right)\left( {x - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\left( {TM} \right)\\x = 3\left( {TM} \right)\end{array} \right.$

Nếu $x < 1$ thì ${\left( {x - 1} \right)^2} =  - 2\left( {x - 1} \right) \Leftrightarrow \left( {x - 1} \right)\left( {x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\left( L \right)\\x =  - 1\left( {TM} \right)\end{array} \right.$

Do đó $\left( 2 \right)$ có $3$ nghiệm phân biệt nên $m = 1$ thỏa bài toán.

+) Nếu $m = \dfrac{1}{2}$ thì $\left( 2 \right)$ trở thành ${\left( {x - 1} \right)^2} = 2\left| {x - \dfrac{1}{2}} \right|$

Nếu $x \ge \dfrac{1}{2}$ thì ${\left( {x - 1} \right)^2} = 2\left( {x - \dfrac{1}{2}} \right) \Leftrightarrow {x^2} - 4x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2 + \sqrt 2 \left( {TM} \right)\\x = 2 - \sqrt 2 \left( {TM} \right)\end{array} \right.$

Nếu $x < \dfrac{1}{2}$ thì ${\left( {x - 1} \right)^2} =  - 2\left( {x - \dfrac{1}{2}} \right) \Leftrightarrow {x^2} = 0 \Leftrightarrow x = 0\left( {TM} \right)$

Do đó $m = \dfrac{1}{2}$ thỏa mãn bài toán.

+) Nếu $m = \dfrac{3}{2}$ thì $\left( 2 \right)$ trở thành ${\left( {x - 1} \right)^2} = 2\left| {x - \dfrac{3}{2}} \right|$

Nếu $x \ge \dfrac{3}{2}$ thì ${\left( {x - 1} \right)^2} = 2\left( {x - \dfrac{3}{2}} \right) \Leftrightarrow {x^2} - 4x + 4 = 0 \Leftrightarrow x = 2\left( {TM} \right)$

Nếu $x < \dfrac{3}{2}$ thì ${\left( {x - 1} \right)^2} =  - 2\left( {x - \dfrac{3}{2}} \right) \Leftrightarrow {x^2} = 2 \Leftrightarrow x =  \pm \sqrt 2 \left( {TM} \right)$

Do đó $m = \dfrac{3}{2}$ thỏa mãn bài toán.

 Vậy các giá trị $m = 1,m = \dfrac{1}{2},m = \dfrac{3}{2}$ đều thỏa mãn.

Điều kiện: $x - m > 0 \Leftrightarrow x > m.$

Đặt: ${2^x} + m = {\log _2}\left( {x - m} \right) = y \Rightarrow \left\{ \begin{array}{l}{2^x} + m = y\\{\log _2}\left( {x - m} \right) = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{2^x} + m = y\\x - m = {2^y}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{2^x} + x = {2^y} + y\;\;\;\;\;\left( * \right)\\m = x - {2^y}\;\;\;\;\;\;\;\;\;\;\;\left( {**} \right)\end{array} \right..$

Xét hàm số đặc trưng: $f\left( t \right) = {2^t} + t$ ta có: $f'\left( t \right) = {2^t}\ln 2 + 1 > 0,\forall t.$

$\Rightarrow f\left( t \right)$ đồng biến trên $R.$

Khi đó ta có: $\left( * \right) \Leftrightarrow f\left( x \right) = f\left( y \right) \Leftrightarrow x = y.$

$\Rightarrow \left( {**} \right) \Leftrightarrow m = x - {2^x}\;\;\;\;\left( {***} \right).$

Xét hàm số: $g\left( x \right) = x - {2^x}$ có: $g'\left( x \right) = 1 - {2^x}\ln 2.$

$\Rightarrow g'\left( x \right) = 0 \Leftrightarrow 1 - {2^x}\ln 2 = 0 \Leftrightarrow {2^x} = \dfrac{1}{{\ln 2}}$ $\Leftrightarrow x = {\log _2}\left( {\dfrac{1}{{\ln 2}}} \right) =  - {\log _2}\left( {\ln 2} \right).$

Ta có BBT:

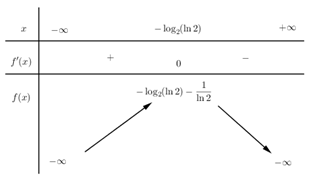
$\Rightarrow \;\left( {***} \right)$ có nghiệm $\Leftrightarrow m \le  - \log { _2}\left( {\ln 2} \right) - \dfrac{1}{{\ln 2}} \approx  - 0,914$

Với $m \in \left( { - 18;\;18} \right)$ và $m \in Z \Rightarrow m \in \left\{ { - 17; - 16;....; - 2; - 1} \right\}.$

Vậy có $17$ giá trị $m$ thỏa mãn.

Ta có: ${\log _{2a + 2b + 1}}\left( {4{a^2} + {b^2} + 1} \right) + {\log _{4ab + 1}}\left( {2a + 2b + 1} \right) = 2$

$\Leftrightarrow {\log _{2a + 2b + 1}}\left( {4{a^2} + {b^2} + 1} \right) + \dfrac{1}{{{{\log }_{2a + 2b + 1}}\left( {4ab + 1} \right)}} = 2.$

Có: ${\left( {2a} \right)^2} + {b^2} \ge 2.2a.b \Leftrightarrow 4{a^2} + {b^2} \ge 4ab.$

$\Rightarrow 4{a^2} + {b^2} + 1 \ge 4ab + 1.$

Dấu “=” xảy ra $\Leftrightarrow 2a = b.$

Theo giả thiết ta có: $\left\{ \begin{array}{l}a > 0\\b > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2a + 2b + 1 > 1\\4ab + 1 > 1\end{array} \right. \Rightarrow \left\{ \begin{array}{ccccc}\log {_{2a + 2b + 1}}\left( {4{a^2} + {b^2} + 1} \right) \ge {\log _{2a + 2b + 1}}\left( {4ab + 1} \right)\\{\log _{4ab + 1}}\left( {2a + 2b + 1} \right) = \dfrac{1}{{{{\log }_{2a + 2b + 1}}\left( {4ab + 1} \right)}}\end{array} \right.$

Áp dụng bất đẳng thức Cauchy ta có:

${\log _{2a + 2b + 1}}\left( {4{a^2} + {b^2} + 1} \right) + \dfrac{1}{{{{\log }_{2a + 2b + 1}}\left( {4ab + 1} \right)}}$$\ge {\log _{2a + 2b + 1}}\left( {4ab + 1} \right) + \dfrac{1}{{{{\log }_{2a + 2b + 1}}\left( {4ab + 1} \right)}}$  $\ge 2.\sqrt {{{\log }_{2a + 2b + 1}}\left( {4ab + 1} \right).\dfrac{1}{{{{\log }_{2a + 2b + 1}}\left( {4ab + 1} \right)}}}  = 2.$

Dấu “=” xảy ra $\Leftrightarrow \left\{ \begin{array}{l}2a = b\\{\log _{2a + 2b + 1}}\left( {4ab + 1} \right) = \dfrac{1}{{{{\log }_{2a + 2b + 1}}\left( {4ab + 1} \right)}}\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}2a = b\\\log _{3b + 1}^2\left( {2{b^2} + 1} \right) = 1\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}2a = b\\{\log _{3b + 1}}\left( {2{b^2} + 1} \right) = 1\end{array} \right.$  (vì ${\log _{3b + 1}}\left( {2{b^2} + 1} \right) > 0$)

$\Leftrightarrow \left\{ \begin{array}{l}b = 2a\\2{b^2} + 1 = 3b + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 2a\\2{b^2} - 3b = 0\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}b = 2a\\\left[ \begin{array}{l}b = 0\;\;\left( {ktm} \right)\\b = \dfrac{3}{2}\;\;\left( {tm} \right)\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{3}{4}\;\;\left( {tm} \right)\\b = \dfrac{3}{2}\end{array} \right.$  

Vậy $a + 2b = \dfrac{3}{4} + 3 = \dfrac{{15}}{4}.$

Điều kiện: $x > 0$ hoặc $- 2 < x <  - \dfrac{1}{2}$ 

$\begin{array}{l}\dfrac{1}{2}{\log _2}\left( {x + 2} \right) + x + 3 = {\log _2}\dfrac{{2x + 1}}{x} + {\left( {1 + \dfrac{1}{x}} \right)^2} + 2\sqrt {x + 2} \\ \Leftrightarrow {\log _2}\sqrt {x + 2}  + x + 2 + 1 - 2\sqrt {x + 2}  = {\log _2}\left( {2 + \dfrac{1}{x}} \right) + 1 + \dfrac{2}{x} + \dfrac{1}{{{x^2}}}\\ \Leftrightarrow {\log _2}\sqrt {x + 2}  + {\left( {\sqrt {x + 2} } \right)^2} - 2\sqrt {x + 2}  = {\log _2}\left( {2 + \dfrac{1}{x}} \right) + \dfrac{2}{x} + \dfrac{1}{{{x^2}}}\\ \Leftrightarrow {\log _2}\sqrt {x + 2}  + {\left( {\sqrt {x + 2} } \right)^2} - 2\sqrt {x + 2}  = {\log _2}\left( {2 + \dfrac{1}{x}} \right) + {\left( {2 + \dfrac{1}{x}} \right)^2} - 2\left( {2 + \dfrac{1}{x}} \right)\;\;\;\left( * \right)\end{array}$

Xét hàm số: $f\left( t \right) = {\log _2}t + {t^2} - 2\sqrt t ,\left( {t > 0} \right).$

Ta có: $f'\left( t \right) = \dfrac{1}{{t.\ln 2}} + 2t - \dfrac{1}{{\sqrt t }} > 0,\forall t > 0$ $\Rightarrow$ Hàm số đồng biến trên $\left( {0; + \infty } \right)$ 

Mà theo $\left( * \right)$ ta có: $f\left( {\sqrt {x + 2} } \right) = f\left( {2 + \dfrac{1}{x}} \right)$

$\begin{array}{l} \Leftrightarrow \sqrt {x + 2}  = 2 + \dfrac{1}{x}\\ \Leftrightarrow x + 2 = 4 + \dfrac{4}{x} + \dfrac{1}{{{x^2}}}\\ \Leftrightarrow {x^3} + 2{x^2} - 4{x^2} - 4x - 1 = 0\\ \Leftrightarrow {x^3} - 2{x^2} - 4x - 1 = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - 3x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1\;\;\;\left( {tm} \right)\\x = \dfrac{{3 + \sqrt {13} }}{2}\;\;\;\left( {tm} \right)\\x = \dfrac{{3 - \sqrt {13} }}{2}\;\;\left( {ktm} \right)\end{array} \right..\\ \Rightarrow S =  - 1 + \dfrac{{3 + \sqrt {13} }}{2} = \dfrac{{1 + \sqrt {13} }}{2}\end{array}$

Ta có $f\left( x \right) = \dfrac{{{4^x}}}{{{4^x} + 2}} \Rightarrow f\left( {1 - x} \right) = \dfrac{{{4^{1\, - \,x}}}}{{{4^{1\, - \,x}} + 2}}$

$\Rightarrow f\left( x \right) + f\left( {1 - x} \right)$$= \dfrac{{{4^x}}}{{{4^x} + 2}} + \dfrac{{{4^{1 - x}}}}{{{4^{1 - x}} + 2}} = \dfrac{{{4^x}}}{{{4^x} + 2}} + \dfrac{4}{{4 + {{2.4}^x}}}$$= \dfrac{{{4^x}}}{{{4^x} + 2}} + \dfrac{2}{{{4^x} + 2}} = 1$

Khi đó $f\left( {\dfrac{1}{{2019}}} \right) + f\left( {\dfrac{{2018}}{{2019}}} \right) = 1;$ $f\left( {\dfrac{2}{{2019}}} \right) + f\left( {\dfrac{{2017}}{{2019}}} \right) = 1;$ … và $f\left( 1 \right) = \dfrac{4}{6}.$

Vậy $S = f\left( {\dfrac{1}{{2019}}} \right) + f\left( {\dfrac{2}{{2019}}} \right) + \,\,...\,\, + f\left( {\dfrac{{2018}}{{2019}}} \right) + f\left( 1 \right) = \dfrac{{2018}}{2}.1 + \dfrac{4}{6} = \dfrac{{3029}}{3}.$

Ta có: $9{x^2} - 4{y^2} = 5 \Leftrightarrow (3x - 2y)(3x + 2y) = 5$$\Leftrightarrow 3x - 2y = \dfrac{5}{{3x + 2y}}$

Khi đó, ta có:

$\begin{array}{l}{\log _m}(3x + 2y) - {\log _3}(3x - 2y) = 1 \Leftrightarrow {\log _m}(3x + 2y) - {\log _3}\dfrac{5}{{3x + 2y}} = 1\\ \Leftrightarrow \dfrac{{{{\log }_3}(3x + 2y)}}{{{{\log }_3}m}} - {\log _3}5 + {\log _3}(3x + 2y) = 1\\ \Leftrightarrow \dfrac{{{{\log }_3}(3x + 2y)}}{{{{\log }_3}m}} = {\log _3}5 - {\log _3}(3x + 2y) + 1\\ \Leftrightarrow {\log _3}m = \dfrac{{{{\log }_3}(3x + 2y)}}{{{{\log }_3}5 - {{\log }_3}(3x + 2y) + 1}}\,\,(1)\end{array}$

Đặt $t = {\log _3}\left( {3x + 2y} \right) \le {\log _3}5$ thì $\left( 1 \right)$ trở thành ${\log _3}m = \dfrac{t}{{{{\log }_3}5 - t + 1}}$

Xét hàm số $y = f(t) = \dfrac{t}{{{{\log }_3}5 - t + 1}},t \in \left( { - \infty ;{{\log }_3}5} \right]$

$f'(t) = \dfrac{{{{\log }_3}5 + 1}}{{{{({{\log }_3}5 - t + 1)}^2}}} > 0,\,\,\forall t \in \left( { - \infty ;{{\log }_3}5} \right]$

Bảng biến thiên:

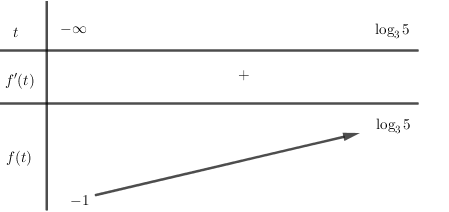
Để $\left( 1 \right)$ có nghiệm thì $- 1 < \log { _3}m \le {\log _3}5\, \Rightarrow \dfrac{1}{3} < m \le 5$

Vậy giá trị lớn nhất của $m$ thỏa mãn yêu cầu đề bài là $5.$

Ta có ${3^x} + {a^x} \ge {6^x} + {9^x} \Leftrightarrow f\left( x \right) = {3^x} + {a^x} - {6^x} - {9^x} \ge 0;\,\,\forall x \in \mathbb{R}.$

Xét $f\left( x \right) = {3^x} + {a^x} - {6^x} - {9^x}$ trên $\mathbb{R},$ có:

$f'\left( x \right) = {3^x}.\ln 3 + {a^x}.\ln a - {6^x}.\ln 6 - {9^x}.\ln 9;$ $f''\left( x \right) = {3^x}{\ln ^2}3 + {a^x}{\ln ^2}a - {6^x}{\ln ^2}6 - {9^x}{\ln ^2}9$

Dễ thấy $f\left( 0 \right) = 0$ nên $f\left( x \right) \ge 0,\forall x \in R \Leftrightarrow f\left( x \right) \ge f\left( 0 \right),\forall x \in R$

Điều này cũng có nghĩa $x = 0$ là điểm cực tiểu của hàm số.

$\Leftrightarrow \left\{ \begin{array}{l}f'\left( 0 \right) = 0\\f''\left( 0 \right) > 0\end{array} \right.$ $\Leftrightarrow \,\left\{ \begin{array}{l}\ln a = \ln \dfrac{{6\,\, \times \,\,9}}{3}\\{\ln ^2}3 + {\ln ^2}a - {\ln ^2}6 - {\ln ^2}9 > 0\end{array} \right.\,$ $\Leftrightarrow a = 18$