Tìm tất cả các giá trị của tham số m để phương trình(3−√5)x2+m(3+√5)x2−2x2−1=0 có đúng hai nghiệm phân biệt?
Trả lời bởi giáo viên
(3−√5)x2+m(3+√5)x2−2x2−1=0⇔(3−√52)x2+m(3+√52)x2−12=0
Ta có (3−√52)x2.(3+√52)x2=(3−√52.3+√52)x2=1
Đặt (3−√52)x2=t⇔(3+√52)x2=1t⇒t=(23+√5)x2⇔x2=log23+√5t, khi đó phương trình trở thành: t+m1t−12=0⇔t2−12t+m=0 ⇔2t2−t+2m=0 ⇔m=t−2t22
Phương trình đã cho có hai nghiệm phân biệt ⇔x2>0⇔log23+√5t>0⇔0<t<1.
(ứng với mỗi nghiệm t thỏa mãn 0<t<1 thì ta có 2 nghiệm x)
Do đó ta cần tìm m để phương trình ẩn t chỉ có 1 nghiệm thuộc (0;1).
Xét hàm f(t)=t−2t22 có f′(t)=1−4t2=0⇔t=14
Bảng biến thiên:
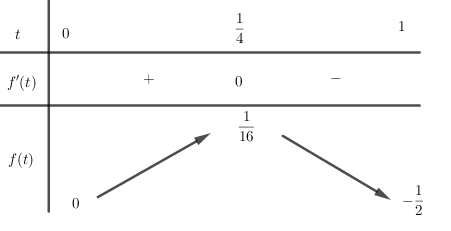
Vậy −12<m≤0 hoặc m=116
Hướng dẫn giải:
+) Đặt (3−√5)x2=t , tìm điều kiện của t
+) Đưa phương trình ban đầu về phương trình bậc 2 ẩn t
+) Tìm điều kiện để phương trình đã cho có hai nghiệm phân biệt ứng với phương trình ẩn t có mấy nghiệm.
+) Cô lập m và tìm điều kiện của m thỏa mãn bài toán.

