Một người nhận hợp đồng dài hạn làm việc cho một công ty với lương tháng đầu là 8 triệu, cứ sau 6 tháng thì tăng lương 10%. Nếu tính theo hợp đồng thì sau đúng 5 năm, người đó nhận được tổng số tiền của công ty là:
5 năm = 60 tháng.
Tháng 1 đến tháng 6: Mỗi tháng nhận được số tiền: 8 (triệu đồng).
Tháng 7 đến tháng 12: Mỗi tháng nhận được số tiền: \(8\left( {1 + 10\% } \right)\) (triệu đồng).
Tháng 13 đến tháng 18: Mỗi tháng nhận được số tiền: \(8\left( {1 + 10\% } \right)\left( {1 + 10\% } \right) = 8{\left( {1 + 10\% } \right)^2}\) (triệu đồng).
…
Tháng 55 đến tháng 60: Mỗi tháng nhận được số tiền: \(8{\left( {1 + 10\% } \right)^9}\) (triệu đồng).
Vậy số tiền người đó nhận được từ công ty sau 5 năm là:
\(\begin{array}{l}6.8 + 6.8\left( {1 + 10\% } \right) + 6.8{\left( {1 + 10\% } \right)^2} + ... + 6.8{\left( {1 + 10\% } \right)^2}\\ = 6.8\left( {1 + 1,1 + 1,{1^2} + ... + 1,{1^9}} \right)\end{array}\)
\( = 48.\dfrac{{1,{1^{10}} - 1}}{{1,1 - 1}} = 480\left( {1,{1^{10}} - 1} \right)\) (triệu đồng).
Bạn An gửi tiết kiệm vào ngân hàng với số tiền là \(1.000.000\) đồng không kì hạn với lãi suất là \(0,65\% \)/ tháng. Tính số tiền bạn An nhận được sau \(2\) năm?
Ta có:
\(\begin{array}{l}A = 1.000.000\\r = 0,65\% \\N = 2.12 = 24\end{array}\)
Vậy \(T = A{\left( {1 + r} \right)^N} = 1.000.000{\left( {1 + 0,65:100} \right)^{24}} = 1.168.236\) (đồng).
Bạn An trúng tuyển đại học nhưng vì không đủ tiền nộp học phí nên An quyết định vay ngân hàng trong 4 năm, mỗi năm 10 triệu đồng với lãi suất 3%/năm (thủ tục vay một năm một lần vào thời điểm đầu năm học). Khi ra trường An thất nghiệp chưa trả được tiền cho ngân hàng nhưng phải chịu lãi suất 8%/năm. Số tiền An nợ ngân hàng bốn năm đại học và một năm thất nghiệp xấp xỉ bằng:
Số tiền An nợ sau 4 năm học đại học là: \({A_4} = \dfrac{{10.\left( {1 + 3\% } \right)\left[ {{{\left( {1 + 3\% } \right)}^4} - 1} \right]}}{{3\% }} \approx 43,09136\) (triệu)
Số tiền An nợ ngân hàng bốn năm đại học và một năm thất nghiệp:
\(43,09136.\left( {1 + 8\% } \right) \approx 46,53867\) (triệu)
Một anh sinh viên \({\rm{T}}\) nhập học đại học vào tháng 8 năm 2020. Bắt đầu từ tháng 9 năm 2020, cứ vào ngày mồng một hàng tháng anh vay ngân hàng 3 triệu đồng với lãi suất cố định \(0,8\% /\) tháng. Lãi tháng trước được cộng vào số nợ để tiếp tục tính lãi cho tháng tiếp theo. Vào ngày mồng một hàng tháng kể từ tháng 9 năm 2022 về sau anh không vay ngân hàng nữa và anh còn trả được cho ngân hàng 2 triệu đồng do việc làm thêm. Hỏi ngay sau ngày anh ra trường \((30/6/2024)\) anh còn nợ ngân hàng bao nhiêu tiền?
Bước 1: Lập công thức tính tổng số tiền vay đến cuối tháng thứ n.
Cuối tháng thứ 1: \({T_1} = a + ar = a(1 + r)\).
Cuối tháng thứ \(2:{T_2} = {T_1} + a + \left( {{T_1} + a} \right) \cdot r\)\( = a \cdot {(1 + r)^2} + a \cdot (1 + r)\).
Tiếp tục như vậy đến cuối tháng \(n:\)\({T_n} = a \cdot {(1 + r)^n} + a \cdot {(1 + r)^{n - 1}}\)\( + \ldots + a \cdot (1 + r)\).
Suy ra \({T_n} = a \cdot (1 + r) \cdot \dfrac{{{{(1 + r)}^n} - 1}}{r}\).
Bước 2: Tính tổng số tiền vay đến cuối tháng \(8/2022\)
Anh sinh viên vay hàng tháng là \(a = 3\) triệu đồng từ tháng \(9/2020\) đến hết tháng 8/2022, tổng cộng 24 tháng.
Vậy tổng số tiền vay đến cuối tháng \(8/2022\) là
\({T_{24}} = 3 \cdot (1 + 0,8\% ) \cdot \dfrac{{{{(1 + 0,8\% )}^{24}} - 1}}{{0,8\% }}\)\( \simeq 79,662\) triệu.
Bước 3: Tính số tiền còn nợ từ tháng \(9/2022\) đến tháng \(6/2024\)
Tính từ cuối tháng 8/2022 anh sinh viên \({\rm{T}}\) thiếu ngân hàng \(A = 79,662\) và bắt đầu trả hàng tháng \(m = 2\) triệu từ tháng \(9/2022\) đến tháng \(6/2024\), tổng cộng được 22 tháng.
Đầu tháng 9/2022: còn nợ \(A - m = 79,662 - 2 = 77,662\) triệu.
Cuối tháng 9/2022: tiền nợ có lãi đến cuối tháng. \({T_1} = 77,662(r + 1)\).
Đầu tháng \(10/2022\) sau khi trả nợ \(m\) thì còn nợ \(77,662(r + 1) - m\).
Cuối tháng 10/2022: còn nợ \({T_2} = [(77,662)(r + 1) - m](1 + r)\)\( = 77,662{(1 + r)^2} - m(1 + r)\).
Cuối tháng \(11/2022\) : còn nợ \({T_3} = 77,662{(1 + r)^3} - m{(1 + r)^2}\)\( - m(1 + r)\).
Tiếp tục như vậy đến cuối tháng \(6/2024\) còn nợ \({T_{22}} = 77,662{(1 + r)^{22}} - m{(1 + r)^{21}}\)\( - m{(1 + r)^{20}} - \ldots - m(1 + r)\)
\( = 77,662{(1 + r)^{22}}\)\( - m \cdot (1 + r)\dfrac{{{{(1 + r)}^{21}} - 1}}{r}\)
\( = 77,662 \cdot {(1 + 0,8\% )^{22}}\)\( - 2 \cdot (1 + 0,8\% ) \cdot \dfrac{{{{(1 + 0,8\% )}^{21}} - 1}}{{0,8\% }}\)\( \simeq 46,64\) triệu đồng
Một người mua xe máy với giá 45 triệu đồng. Biết rằng giá trị khấu hao tài sản xe giảm 60% mỗi năm. Hỏi sau bao nhiêu năm thì giá trị xe chỉ còn 5 triệu đồng?
Gọi số năm để xe có giá trị 5 triệu đồng là \(n\left( {n \in {N^*}} \right)\)
Sau \(n\) năm giá trị xe còn lại là: \({T_n} = {T_0}{\left( {1 - 60\% } \right)^n}\) với \({T_n}\) là giá xe sau \(n\) năm, \({T_o}\) là giá xe ban đầu
Khi đó ta có: \(5 = 45.0,{4^n} \Rightarrow 0,{4^n} = \dfrac{1}{9}\) nên \(n = {\log _{0,4}}\dfrac{1}{9} \approx 2,39\)
Vậy sau 2,5 năm giá trị xe chỉ còn 5 triệu đồng
Một thầy giáo cứ đầu mỗi tháng lại gửi ngân hàng 8000000 VNĐ với lãi suất \(0,5\% \)/ tháng. Hỏi sau bao nhiêu tháng thầy giáo có thể tiết kiệm tiền để mua được một chiếc xeô tô trị giá 400 000 000 VNĐ?
\(T = \dfrac{A\left( {1 + r} \right)}{r}\left[ {{{\left( {1 + r} \right)}^n} - 1} \right]\)
..
\( \Leftrightarrow {\left( {1 + 0,5\% } \right)^n} - 1 \approx 0,249\)\( \Leftrightarrow {\left( {1 + 0,5\% } \right)^n} = 1,249\)
\( \Leftrightarrow n = {\log _{1 + 0,5\% }}1,249\)\( \Leftrightarrow n \approx 44,58\)
\( \Rightarrow \) Sau ít nhất \(n = 45\) tháng thầy giáo có thể tiết kiệm tiền mua xe
Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền \(T\) theo hình thức lãi kép với lãi suất \(0,6\% \) mỗi tháng. Biết sau \(15\) tháng người đó có số tiền là \(10\) triệu đồng. Hỏi số tiền \(T\) gần với số tiền nào nhất trong các số sau.
\(P = \dfrac{T\left( {1 + r} \right)}{r}\left[ {{{\left( {1 + r} \right)}^n} - 1} \right]\)
\( \Leftrightarrow {10^7} = \dfrac{T}{{0,6\% }}\left[ {{{\left( {1 + 0,6\% } \right)}^{15}} - 1} \right]\left( {1 + 0,6\% } \right)\)
\( \Leftrightarrow T = 635301,4591\)\( \approx 635000\) đồng
Một người muốn có 1 tỉ tiền tiết kiệm sau 6 năm gửi ngân hàng bằng cách bắt đầu từ ngày 01/01/2019 đến 31/12/2024, vào ngày 01/01 hàng năm người đó gửi vào ngân hàng một số tiền bằng nhau với lãi suất ngân hàng là 7% /1 năm (tính từ ngày 01/01 đến ngày 31/12) và lãi suất hàng năm được nhập vào vốn. Hỏi số tiền mà người đó phải gửi vào ngân hàng hàng năm là bao nhiêu (với giả thiết lãi suất không thay đổi và số tiền được làm tròn đến đơn vị đồng)?
Áp dụng công thức lãi kép: \(T = \dfrac{A\left( {1 + r} \right)}{r}\left[ {{{\left( {1 + r} \right)}^n} - 1} \right]\)
\( \Leftrightarrow {10^9} = \dfrac{A}{{7\% }}\left[ {{{\left( {1 + 7\% } \right)}^6} - 1} \right]\left( {1 + 7\% } \right)\)\( \Leftrightarrow A = 130650280,1\)\( \approx 130650280\)
Một người gửi tiết kiệm ngân hàng, mỗi tháng gửi 1 triệu đồng, với lãi suất kép 1% trên tháng. Gửi được hai năm 3 tháng người đó có công việc nên đã rút toàn bộ gốc và lãi về. Số tiền người đó được rút là
Hai năm ba tháng \( = \) 27 tháng
\(T = \dfrac{A}{r}\left[ {{{\left( {1 + r} \right)}^n} - 1} \right]\left( {1 + r} \right)\)\( \Leftrightarrow T = \dfrac{1}{{1\% }}\left[ {{{\left( {1 + 1\% } \right)}^{27}} - 1} \right]\left( {1 + 1\% } \right)\)
\( \Leftrightarrow T = 100\left[ {{{\left( {1,01} \right)}^{27}} - 1} \right]1,01\)\( \Leftrightarrow T = 101\left[ {{{\left( {1,01} \right)}^{27}} - 1} \right]\) (triệu đồng)
Một người lần đầu gửi ngân hàng \(100\) triệu đồng với kì hạn \(3\) tháng, lãi suất \(3\% \) của một quý và lãi từng quý sẽ được nhập vào vốn (hình thức lãi kép). Sau đúng \(6\) tháng, người đó gửi thêm \(100\) triệu đồng với kì hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được 1 năm kể từ khi gửi thêm tiền lần hai sẽ gần với kết quả nào sau đây?
1 quý \( = \) 3 tháng nên 6 tháng \( = \) 2 quý
1 năm \( = \) 4 quý
\( + )\) Sau 6 tháng, người đó thu được: \(100{\left( {1 + 3\% } \right)^2} = 106,09\) (triệu đồng)
\( + )\) Người đó gửi thêm 100 triệu nên tổng số tiền bằng: \(106,09 + 100 = 206,09\) (triệu đồng)
\( + )\) Số tiền sau 1 năm nữa là: \(206,09{\left( {1 + 3\% } \right)^4} \approx 232\) (triệu đồng)
Một người gửi tiết kiệm vào ngân hàng A với số tiền là 100 triệu đồng với lãi suất mỗi quý (3 tháng) là \(2,1\% \). Số tiền lãi được cộng vào vốn sau mỗi quý. Sau 2 năm người đó vẫn tiếp tục gửi tiết kiệm số tiền thu được từ trên nhưng với lãi suất \(1,1\% \) mỗi tháng. Số tiền lãi được cộng vào vốn sau mỗi tháng. Hỏi sau 3 năm kể từ ngày gửi tiết kiệm lần thứ hai vào ngân hàng A người đó thu được số tiền gần nhất với giá trị nào sau đây?
\( + )\) Số tiền người đó nhận được sau 2 năm đầu (8 quý đầu) gửi tiền là:
\(T = P{\left( {1 + r} \right)^n}\)\( = 100{\left( {1 + 2,1\% } \right)^8} = 118,088\) (triệu đồng)
\( + )\) Số tiền người đó nhận được sau 3 năm tiếp theo gửi tiền là:
\(118,088{\left( {1 + 1,1\% } \right)^{3.12}} = 175,08\) (triệu đồng)
Anh An gửi số tiền 58 triệu đồng vào một ngân hàng theo hình thức lãi kép và ổn định trong 9 tháng thì lĩnh về được 61758000đ. Hỏi lãi suất ngân hàng hàng tháng là bao nhiêu? Biết rằng lãi suất không thay đổi trong thời gian gửi.
Ta có: \(T = A{\left( {1 + r} \right)^n}\)
\( \Leftrightarrow 61,758 = 58{\left( {1 + r} \right)^9}\)
Nhập phương trình vào máy tính:
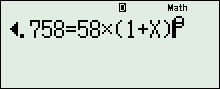
Bấm SHIFT + CALC (Solve), nhập bừa \(X = 2\), rồi nhấn “ = “
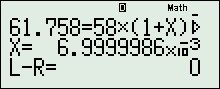
Lấy kết quả trên nhân 100 \( \Rightarrow \)\(r = 0,7\% \) .
Ông Nam dự định gửi vào ngân hàng một số tiền với lãi suất \(6,6\% \) /năm. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho năm tiếp theo. Tính số tiền tối thiểu \(x\) triệu đồng \(\left( {x \in \mathbb{N}} \right)\) ông Nam gửi vào ngân hàng để sau \(3\) năm số tiền lãi đủ mua một chiếc xe gắn máy trị giá \(26\) triệu đồng.
Áp dụng công thức lãi kép: \(T = A{\left( {1 + r} \right)^n}\)
\( + )\) Số tiền lãi ông Nam thu được sau 3 năm là: \(T - A = A{\left( {1 + r} \right)^n} - A\)
\( + )\) Số tiền lãi đủ mua chiếc xe 26 triệu đồng khi: \(A{\left( {1 + r} \right)^n} - A \ge 26\)
\( \Leftrightarrow A{\left( {1 + 6,6\% } \right)^3} - A \ge 26\)\( \Leftrightarrow A \ge 123,01\)
\( \Rightarrow \) Tối thiểu ông A phải gửi 124 triệu đồng
Năm 2020, một doanh nghiệp X có tổng doanh thu là 150 tỉ đồng. Dự kiến trong 10 năm tiếp theo, tổng doanh thu mỗi năm sẽ tăng thêm \(12\% \) so với năm liền trước. Theo dự kiến đó thì kể từ năm nào, tổng doanh thu của doanh nghiệp \({\rm{X}}\) vượt quá 360 tỉ đồng?
Ta có tổng doanh thu của doanh nghiệp \({\rm{X}}\) tại năm thứ \(n\) là:
\(T = 150{(1 + 0,12)^n} = 150.1,{12^n}.\)
Để tổng doanh thu vượt quá 360 tỉ đồng thì
\(150.1,{12^n} > 360\)\( \Leftrightarrow n > {\log _{1,12}}\left( {\dfrac{{360}}{{150}}} \right)\)\( \Rightarrow n > 7,725\)
Do \(n\) nguyên nên \(n = 8\).
Vậy kể từ năm 2028 doanh thu của doanh nghiệp X sẽ vượt quá 360 tỉ đồng
Một kĩ sư mới ra trường làm việc với mức lương khởi điểm là 7 triệu đồng/tháng. Cứ sau 9 tháng làm việc, mức lương của kĩ sư đó lại được tăng thêm \(10\% \). Hỏi sau 4 năm làm việc, tổng số tiền lương kĩ sư đó nhận được là bao nhiêu?
Bốn năm có 48 tháng.
Tổng tiền lương 9 tháng đầu là \(9 \cdot 7 \cdot {10^6}\) đồng.
Tiền lương tháng 10 là \({7.10^6}(1 + 10\% ) = {7.10^6}.1,1\) đồng.
Tổng tiền lương từ tháng 10 đến tháng 18 là \(9.7 \cdot {10^6} \cdot 1,1\) đồng.
Tiền lương tháng thứ 19 là \(7 \cdot {10^6}{(1 + 10\% )^2} = 7 \cdot {10^6} \cdot 1,{1^2}\) đồng.
Tổng tiền lương từ tháng 19 đến tháng 27 là \({9.7.10^6} \cdot 1,{1^2}\) dồng.
Tiền lương tháng thứ 28 là \(7 \cdot {10^6}{(1 + 10\% )^3} = 7 \cdot {10^6} \cdot 1,{1^3}\) đồng.
Tổng tiền lương từ tháng 28 đến tháng 36 là \({9.7.10^6}.1,{1^3}\) dồng.
Tiền lương tháng 37 là \(7 \cdot {10^6}{(1 + 10\% )^4} = 7 \cdot {10^6} \cdot 1,{1^4}\) đồng.
Tổng tiền lương từ tháng thứ 37 đến tháng 45 là \({9.7.10^6} \cdot 1,{1^4}\) đồng.
Tiền lương tháng thứ 46 là \({7.10^6}{(1 + 10\% )^5} = {7.10^6}.1,{1^5}\) đồng.
Tổng tiền lương từ tháng 46 đến tháng 48 là \({3.7.10^6}.1,{1^5}\) đồng.
Tổng tiền lương sau 4 năm (từ tháng 1 đến tháng 48) là 418442010 đồng.
Một người gửi 100 triệu đồng vào ngân hàng theo thể thức lãi kép kỳ hạn 1 năm với lãi suất 7, 8% /năm. Giả sử lãi suất không thay đổi. Sau 5 năm thì người đó nhận về số tiền kể cả gốc và lãi (làm tròn đến hàng nghìn đồng) là
Ta có:
\(A = {100.10^9}\)(đồng)
\(\begin{array}{l}r = 7,8\% \\N = 5\end{array}\)
Vậy \(T = A.{\left( {1 + r} \right)^N}\) \( = {100.10^9}.{\left( {1 + 7,8\% } \right)^5} \approx 145577348\)(đồng)
Một người mua một căn hộ chung cư với giá 500 triệu đồng. Người đó trả trước số tiền là 100 triệu đồng. Số tiền còn lại người đó thanh toán theo hình thức trả góp với lãi suất tính trên tổng số tiền còn nợ là \(0,5\% \) mỗi tháng. Kể từ ngày mua, sau đúng mỗi tháng người đó trả số tiền cố định là 4 triệu đồng. Thời gian để người đó trả hết nợ là
Bước 1: Biểu diễn số tiền người đó nợ hết tháng thứ n theo n.
Tổng số tiền người đó còn nợ là \({A_0} = 400\) triệu đồng.
Số tiền người đó còn nợ hết tháng thứ nhất là: \({A_1} = {A_0} + 0,5\% {A_0} - 4 = 1,005{A_0} - 4\).
Số tiền người đó còn nợ hết tháng thứ hai là: \({A_2} = {A_1} + 0,5\% {A_1} - 4 = 1,005{A_1} - 4\) \( = 1,005\left( {1,005{A_0} - 4} \right) - 4 = {(1,005)^2}{A_0} - 4(1,005 + 1)\).
Số tiền người đó còn nợ hết tháng thứ ba là: \({A_3} = {A_2} + 0,5\% {A_2} - 4 = 1,005{A_2} - 4\) \( = 1,005\left[ {{{(1,005)}^2}{A_0} - 4(1,005 + 1)} \right] - 4 = {(1,005)^3}{A_0} - 4\left[ {{{(1,005)}^2} + 1,005 + 1} \right].\)
Số tiền người đó còn nợ hết tháng thứ \(n\) là:
\({A_n} = {(1,005)^n}{A_0} - 4\left[ {{{(1,005)}^{n - 1}} + {{(1,005)}^{n - 2}} + \ldots + 1} \right]\).
Bước 2: Sử dụng công thức tổng n số hạng đầu tiên của cấp số nhân.
Ta có: \(1 + 1,005 + {(1,005)^2} + \ldots + {(1,005)^{n - 2}} + {(1,005)^{n - 1}}\) là tổng \(n\) số hạng của một cấp số nhân có số hạng đầu \({u_1} = 1\) và \(q = 1,005\).
Do đó \({S_n} = \dfrac{{1\left[ {1 - {{(1,005)}^n}} \right]}}{{1 - 1,005}} = 200\left[ {{{(1,005)}^n} - 1} \right]\).
Bước 3: Lập phương trình ẩn n rồi tìm n.
Người đó trả hết nợ khi \({A_n} = 0 \Rightarrow {(1,005)^n}{A_0} - 800\left[ {{{(1,005)}^n} - 1} \right] = 0\)
\({400.(1,005)^n} = 800 \Leftrightarrow {(1,005)^n} = 2 \Leftrightarrow n = {\log _{1,005}}2 \approx 138,98\) (tháng).
Vậy người đó trả hết nợ sau 139 tháng.
Ông An lập cuốn sổ tiết kiệm ở một ngân hàng số tiền gốc ban đầu là \(200\) triệu đồng với lãi suất cố định \(0,54\% /\)tháng. Cứ đều đặn sau mỗi tháng, kể từ ngày gửi, ông An rút \(5\) triệu ra để chi phí cho sinh hoạt gia đình. Biết rằng mỗi tháng ngân hàng tính lãi cho ông An theo số tiền còn lại. Hỏi sau đúng \(3\) năm, số tiền còn lại trong ngân hàng của ông An gần nhất với số tiền nào dưới đây?
Số tiền còn lại của ông An sau 3 năm tức 36 tháng là
\(M = 200{\left( {1 + 0,54\% } \right)^{36}} - 5.\dfrac{{{{\left( {1 + 0,54\% } \right)}^{36}} - 1}}{{0,54\% }} \approx 44,7\) triệu.
Một người gửi tiết kiệm vào ngân hàng một số tiền, lãi suất mỗi tháng là \(r\), gửi theo hình thức lãi kép không kì hạn. Sau \(N\) tháng người đó rút ra cả vốn lẫn lãi được số tiền \(T\) đồng. Công thức tính số tiền \(A\) gửi vào ban đầu là:
Từ công thức lãi kép \(T = A{\left( {1 + r} \right)^N}\) ta suy ra \(A = \dfrac{T}{{{{\left( {1 + r} \right)}^N}}}\)
Ông Tuấn gửi 9,8 triệu đồng với lãi suất 8,4% /năm và lãi hằng năm được nhập vào vốn. Hỏi theo cách đó thì sau bao nhiêu năm người đó thu được tổng số 20 triệu đồng (biết lãu suất không thay đổi)?
Theo công thức lãi kép ta có:
\(\begin{array}{l}\,\,\,\,\,T = A{\left( {1 + r} \right)^n}\\ \Leftrightarrow 20 = 9,8{\left( {1 + 8.4\% } \right)^n} \Leftrightarrow n = {\log _{1,084}}\dfrac{{20}}{{9,8}} \approx 8,84\end{array}\)
Vậy phải sau ít nhất 9 năm người đó mới thu được 20 triệu đồng.

