Một chất điểm \(A\) xuất phát từ \(O\), chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v(t) = \dfrac{1}{{150}}{t^2} + \dfrac{{59}}{{75}}t(\;m/s)\), trong đó \(t\) là khoảng thời gian tính từ lúc \(A\) bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm \(B\) cũng xuất phát từ \(O\), chuyển động thẳng cùng hướng với \(A\) nhưng chậm hơn 3 giây so với \(A\) và có gia tốc bằng \(a\left( {\;m/{s^2}} \right)\) ( \(a\) là hằng số). Sau khi \(B\) xuất phát được 12 giây thì đuổi kịp \(A\). Vận tốc của \(B\) tại thời điểm đuổi kịp \(A\) bằng
Bước 1: Tìm thời gian của A và B đi được khi 2 chất điểm gặp nhau.
+) Từ đề bài, ta suy ra: tính từ lúc chất điểm \(A\) bắt đầu chuyển động cho đến khi bị chất điểm \(B\) bắt kịp thì \(A\) đi được 15 giây, \(B\) đi được 12 giây.
Bước 2: Biểu diễn \({v_B}\) theo thời gian t và gia tốc a. Lập phương trình tìm a rồi tìm vận tốc.
+) Biểu thức vận tốc của chất điểm \(B\) có dạng \({v_B}(t) = \int a dt = at + C\), lại có \({v_B}(0) = 0\)
nên \({v_B}(t) = at\).
Quãng đường hai chất điểm đi được là bằng quãng đường hai chất điểm đi được là bằng nhau. Do đó
\(\int_0^{15} {\left( {\dfrac{1}{{150}}{t^2} + \dfrac{{59}}{{75}}t} \right)} dt = \int_0^{12} a tdt \Leftrightarrow 96 = 72a \Leftrightarrow a = \dfrac{4}{3}\)
Từ đó, vận tốc của \(B\) tại thời điểm đuổi kịp \(A\) bằng \({v_B}(12) = \dfrac{4}{3} \cdot 12 = 16(\;m/s)\).
Dòng điện xoay chiều hình sin chạy qua mạch dao động LC lí tưởng có phương trình \(i = {I_0}\sin \left( {wt + \dfrac{\pi }{2}} \right)\). Ngoài ra \(i = {q^\prime }(t)\) với \(q\) là điện tích tức thời trong tụ. Tính từ lúc \(t = 0\), điện lượng chuyển qua tiết diện thẳng của dây dẫn của mạch trong thời gian \(\dfrac{\pi }{{2w}}\) là
Tính từ lúc \(t = 0\), điện lượng chuyển qua tiết diện thẳng của dây dẫn của mạch trong thời gian \(\dfrac{\pi }{{2w}}\) là \(q = \int_0^{\dfrac{\pi }{{2w}}} {{I_0}} \sin \left( {wt + \dfrac{\pi }{2}} \right)dt\)\( = - \left. {\dfrac{{{I_0}}}{w}\cos \left( {wt + \dfrac{\pi }{2}} \right)} \right|_0^{\dfrac{\pi }{{2w}}}\)
\( = - \dfrac{{{I_0}}}{w}\left[ {\cos \left( {w \cdot \dfrac{\pi }{{2w}} + \dfrac{\pi }{2}} \right) - \cos \left( {w.0 + \dfrac{\pi }{2}} \right)} \right]\)\( = - \dfrac{{{I_0}}}{w}\left[ {\cos \pi - \cos \left( {\dfrac{\pi }{2}} \right)} \right] = \dfrac{{{I_0}}}{w}\)
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( 0 \right) = 3\) và \(f\left( x \right) + f\left( {2 - x} \right) = {x^2} - 2x + 2\,\,\forall x \in \mathbb{R}\). Tích phân \(\int\limits_0^2 {xf'\left( x \right)dx} \) bằng:
\(\int\limits_0^2 {xf'\left( x \right)dx} = \int\limits_0^2 {xd\left( {f\left( x \right)} \right)} = \left. {xf\left( x \right)} \right|_0^2 - \int\limits_0^2 {f\left( x \right)dx} = 2f\left( 2 \right) - \int\limits_0^2 {f\left( x \right)dx} \)
Theo bài ra ta có:
\(f\left( x \right) + f\left( {2 - x} \right) = {x^2} - 2x + 2\,\,\forall x \in \mathbb{R} \Rightarrow f\left( 0 \right) + f\left( 2 \right) = 2 \Rightarrow f\left( 2 \right) = 2 - f\left( 0 \right) = - 1\).
\( \Rightarrow \int\limits_0^2 {xf'\left( x \right)dx} = - 2 - \int\limits_0^2 {f\left( x \right)dx} = - 2 - \int\limits_0^2 {f\left( t \right)dt} \).
Đặt \(t = 2 - x \Rightarrow dt = - dx\). Đổi cận \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 2\\x = 2 \Rightarrow t = 0\end{array} \right.\).
\(\begin{array}{l} \Rightarrow \int\limits_0^2 {f\left( t \right)dx} = - \int\limits_2^0 {f\left( {2 - x} \right)dx} = \int\limits_0^2 {f\left( {2 - x} \right)dx} \\ \Rightarrow \int\limits_0^2 {f\left( x \right)dx} = \int\limits_0^2 {f\left( {2 - x} \right)dx} \\ \Rightarrow 2\int\limits_0^2 {f\left( x \right)dx} = \int\limits_0^2 {f\left( x \right)dx} + \int\limits_0^2 {f\left( {2 - x} \right)dx} \\ \Rightarrow 2\int\limits_0^2 {f\left( x \right)dx} = \int\limits_0^2 {\left[ {f\left( x \right) + f\left( {2 - x} \right)} \right]dx} \\ \Rightarrow 2\int\limits_0^2 {f\left( x \right)dx} = \int\limits_0^2 {\left( {{x^2} - 2x + 2} \right)dx} \\ \Rightarrow 2\int\limits_0^2 {f\left( x \right)dx} = \left. {\left( {\dfrac{{{x^3}}}{3} - {x^2} + 2x} \right)} \right|_0^2 = \dfrac{8}{3}\\ \Rightarrow \int\limits_0^2 {f\left( x \right)dx} = \dfrac{4}{3}\end{array}\)
Vậy \(\int\limits_0^2 {xf'\left( x \right)dx} = - 2 - \dfrac{4}{3} = - \dfrac{{10}}{3}\).
Cho \(f\left( x \right)\) là hàm liên tục trên đoạn \(\left[ {0;a} \right]\) thỏa mãn \(\left\{ {\begin{array}{*{20}{c}}{f\left( x \right).f\left( {a - x} \right) = 1}\\{f\left( x \right) > 0,\forall x \in \left[ {0;a} \right]}\end{array}} \right.\) và \(\int\limits_0^a {\dfrac{{{\rm{d}}x}}{{1 + f\left( x \right)}}} = \dfrac{{ba}}{c},\) trong đó \(b\), \(c\) là hai số nguyên dương và \(\dfrac{b}{c}\) là phân số tối giản. Khi đó \(b + c\) có giá trị thuộc khoảng nào dưới đây?
Đặt \(t = a - x \Rightarrow {\rm{d}}t = - {\rm{d}}x\)
Đổi cận \(x = 0 \Rightarrow t = a;x = a \Rightarrow t = 0.\)
Lúc đó \(I = \int\limits_0^a {\dfrac{{{\rm{d}}x}}{{1 + f\left( x \right)}}} = \int\limits_a^0 {\dfrac{{ - {\rm{d}}t}}{{1 + f\left( {a - t} \right)}}} = \int\limits_0^a {\dfrac{{{\rm{d}}x}}{{1 + f\left( {a - x} \right)}} = \int\limits_0^a {\dfrac{{{\rm{d}}x}}{{1 + \dfrac{1}{{f\left( x \right)}}}} = \int\limits_0^a {\dfrac{{f\left( x \right){\rm{d}}x}}{{1 + f\left( x \right)}}} } } \)
Suy ra \(2I = I + I = \int\limits_0^a {\dfrac{{{\rm{d}}x}}{{1 + f\left( x \right)}} + \int\limits_0^a {\dfrac{{f\left( x \right){\rm{d}}x}}{{1 + f\left( x \right)}} = \int\limits_0^a {1{\rm{d}}x} } = a} \)
Do đó \(I = \dfrac{1}{2}a \Rightarrow b = 1;c = 2 \Rightarrow b + c = 3.\)
Một chất điểm đang chuyển động với vận tốc \({v_0} = 15\;{\rm{m/s}}\) thì tăng tốc với gia tốc \(a\left( t \right) = {t^2} + 4t\;\left( {{\rm{m/}}{{\rm{s}}^2}} \right)\). Tính quãng đường chất điểm đó đi được trong khoảng thời gian \(3\) giây kể từ lúc bắt đầu tăng vận tốc.
\(a\left( t \right) = {t^2} + 4t\) \( \Rightarrow v\left( t \right) = \int {a\left( t \right){\rm{d}}t} = \dfrac{{{t^3}}}{3} + 2{t^2} + C{\rm{ }}\)\(\left( {C \in \mathbb{R}} \right)\).
Mà \(v\left( 0 \right) = C = 15\) \( \Rightarrow v\left( t \right) = \dfrac{{{t^3}}}{3} + 2{t^2} + 15\).
Vậy $S = \int\limits_0^3 {\left( {\dfrac{{{t^3}}}{3} + 2{t^2} + 15} \right)dt} = 69,75\;{\rm{m}}$.
Bác Năm làm một cái cửa nhà hình parabol bằng gỗ có chiều cao từ mặt đất đến đỉnh là \(2,25\) mét, chiều rộng tiếp giáp với mặt đất là \(3\) mét. Giá tiền mỗi mét vuông gỗ là \(1500000\) đồng. Vậy số tiền bác Năm phải trả là:
Gọi phương trình parabol \(\left( P \right):y = a{x^2} + bx + c\). Do tính đối xứng của parabol nên ta có thể chọn hệ trục tọa độ \(Oxy\) sao cho \(\left( P \right)\) có đỉnh $I\left( {0;\dfrac{9}{4}} \right)\in Oy $ và đi qua hai điểm $A\left( { - \dfrac{3}{2};0} \right),B\left( {\dfrac{3}{2};0} \right)$ (như hình vẽ).
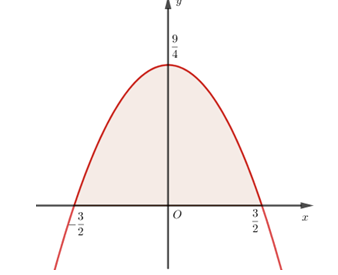
Ta có hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{9}{4} = c,\left( {I \in \left( P \right)} \right)\\\dfrac{9}{4}a - \dfrac{3}{2}b + c = 0\left( {A \in \left( P \right)} \right)\\\dfrac{9}{4}a + \dfrac{3}{2}b + c = 0\left( {B \in \left( P \right)} \right)\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}c = \dfrac{9}{4}\\a = - 1\\b = 0\end{array} \right.\)
Vậy \(\left( P \right):y = - {x^2} + \dfrac{9}{4}\)
Dựa vào đồ thị, diện tích cửa parabol là:
\(S = \int\limits_{\frac{{ - 3}}{2}}^{\frac{3}{2}} {\left( { - {x^2} + \dfrac{9}{4}} \right){d}x} \)\( = 2\int\limits_0^{\frac{3}{2}} {\left( { - {x^2} + \dfrac{9}{4}} \right){d}x} \)$ = \left. {2\left( {\dfrac{{ - {x^3}}}{3} + \dfrac{9}{4}x} \right)} \right|_0^{\frac{9}{4}}$ \( = \dfrac{9}{2}{{\rm{m}}^2}\)
Số tiền phải trả là: \(\dfrac{9}{2}.1500000 = 6750000\) đồng
Cho hình phẳng \(D\) giới hạn bởi đường cong \(y = {{\rm{e}}^{x - 1}}\), các trục tọa độ và phần đường thẳng \(y = 2 - x\) với \(x \ge 1\). Tính thể tích khối tròn xoay tạo thành khi quay quanh trục hoành.
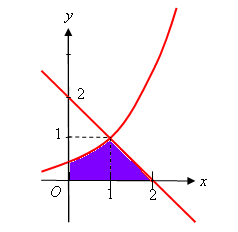
Phương trình hoành độ giao điểm của đường cong \(y = {{\rm{e}}^{x - 1}}\) và đường thẳng \(y = 2 - x\): ${{\rm{e}}^{x - 1}} = 2 - x \Leftrightarrow x = 1$.
(Vì \(y = {{\rm{e}}^{x - 1}}\) là hàm đồng biến và \(y = 2 - x\) là hàm nghịch biến trên tập xác định \(\mathbb{R}\) nên phương trình có tối đa \(1\) nghiệm. Mặt khác $x = 1$ thỏa mãn pt nên đó là nghiệm duy nhất của pt đó).
Đường thẳng \(y = 2 - x\) cắt trục hoành tại điểm có hoành độ \(x = 2\).
\(V = \pi \int\limits_0^1 {{{\left( {{{\rm{e}}^{x - 1}}} \right)}^2}{\rm{d}}x} + \pi \int\limits_1^2 {{{\left( {2 - x} \right)}^2}{\rm{d}}x} \)\( = \left. \dfrac{1}{2}{\pi {{\rm{e}}^{2x - 2}}} \right|_0^1 + \left. {\pi \left( {\dfrac{{{x^3}}}{3} - 2x + 4} \right)} \right|_1^2 = \dfrac{{\pi \left( {5{{\rm{e}}^2} - 3} \right)}}{{6{{\rm{e}}^2}}}\)
Xét hàm số $y = f\left( x \right)$ liên tục trên miền $D = \left[ {a,b} \right]$ có đồ thị là một đường cong $C$. Gọi $S$ là phần giới hạn bởi $C$ và các đường thẳng $x = a$, $x = b$. Người ta chứng minh được rằng độ dài đường cong $S$ bằng $\int\limits_a^b {\sqrt {1 + {{\left( {f'\left( x \right)} \right)}^2}} {\rm{d}}x} $. Theo kết quả trên, độ dài đường cong $S$ là phần đồ thị của hàm số $f\left( x \right) = \ln x$ bị giới hạn bởi các đường thẳng $x = 1$, $x = \sqrt 3 $ là $m - \sqrt m + \ln \dfrac{{1 + \sqrt m }}{{\sqrt n }}$ với $m$, $n \in \mathbb{Z}$ thì giá trị của ${m^2} - mn + {n^2}$ là bao nhiêu?
Ta có $f'\left( x \right) = \dfrac{1}{x}$.
Khi đó, độ dài đường cong $S$ là $l = \int\limits_1^{\sqrt 3 } {\sqrt {1 + \dfrac{1}{{{x^2}}}} {\rm{d}}x} = \int\limits_1^{\sqrt 3 } {\dfrac{{\sqrt {1 + {x^2}} }}{x}{\rm{d}}x} = \int\limits_1^{\sqrt 3 } {\dfrac{{\sqrt {1 + {x^2}} }}{{{x^2}}}x{\rm{d}}x} $.
Đặt $t = \sqrt {1 + {x^2}} $. Suy ra: ${t^2} = 1 + {x^2}$$ \Rightarrow t{\rm{d}}t = x{\rm{d}}x$.
Đổi cận: $x = 1 \Rightarrow t = \sqrt 2 $; $x = \sqrt 3 \Rightarrow t = 2.$
Suy ra: $l = \int\limits_{\sqrt 2 }^2 {\dfrac{{{t^2}}}{{{t^2} - 1}}{\rm{d}}t} = \int\limits_{\sqrt 2 }^2 {\left( {1 + \dfrac{1}{{\left( {t - 1} \right)\left( {t + 1} \right)}}} \right){\rm{d}}t} = \left. t \right|_{\sqrt 2 }^2 + \dfrac{1}{2}\left. {\ln \left| {\dfrac{{t - 1}}{{t + 1}}} \right|} \right|_{\sqrt 2 }^2$.
Suy ra: $l = 2 - \sqrt 2 + \dfrac{1}{2}\left( {\ln \dfrac{1}{3} - \ln \left( {3 - 2\sqrt 2 } \right)} \right) = 2 - \sqrt 2 + \dfrac{1}{2}\ln \dfrac{{3 + 2\sqrt 2 }}{3} = 2 - \sqrt 2 + \ln \dfrac{{1 + \sqrt 2 }}{{\sqrt 3 }}$
Mà $l = m - \sqrt m + \ln \dfrac{{1 + \sqrt m }}{{\sqrt n }}$ nên suy ra $\left\{ \begin{array}{l}m = 2\\n = 3\end{array} \right.$.
Vậy ${m^2} - mn + {n^2} = 7$.
Tìm tất cả các giá trị thực của tham số $m$ để phương trình $5{x^2} + 12x + 16 = m\left( {x + 2} \right)\sqrt {{x^2} + 2} $ có hai nghiệm thực phân biệt thỏa mãn điều kiện ${2017^{2x + \sqrt {x + 1} }} - {2017^{2 + \sqrt {x + 1} }} + 2018x \le 2018$.
Ta có ${2017^{2x + \sqrt {x + 1} }} - {2017^{2 + \sqrt {x + 1} }} + 2018x \le 2018$
$ \Leftrightarrow {2017^{2x + \sqrt {x + 1} }} + 1009\left( {2x + \sqrt {x + 1} } \right) \le {2017^{2 + \sqrt {x + 1} }} + 1009\left( {2 + \sqrt {x + 1} } \right)$$ \Leftrightarrow f\left( {2x + \sqrt {x + 1} } \right) \le f\left( {2 + \sqrt {x + 1} } \right)$
Xét hàm số $f\left( u \right) = {2017^u} + 1009u$
Ta có $f'\left( t \right) = {2017^u}\ln 2017 + 1009 > 0,\forall u$$ \Rightarrow f\left( u \right)$ đồng biến.
Nên $2x + \sqrt {x + 1} \le 2 + \sqrt {x + 1} \Leftrightarrow - 1 \le x \le 1$
Ta lại có $5{x^2} + 12x + 16 = m\left( {x + 2} \right)\sqrt {{x^2} + 2} $$ \Leftrightarrow 3{\left( {x + 2} \right)^2} + 2\left( {{x^2} + 2} \right) = m\left( {x + 2} \right)\sqrt {{x^2} + 2} $
$ \Rightarrow 3{\left( {\dfrac{{x + 2}}{{\sqrt {{x^2} + 2} }}} \right)^2} + 2 = m.\dfrac{{x + 2}}{{\sqrt {{x^2} + 2} }}$
Xét $t = \dfrac{{x + 2}}{{\sqrt {{x^2} + 2} }} \Rightarrow t'\left( x \right) = \dfrac{{2 - 2x}}{{{{\left( {\sqrt {{x^2} + 2} } \right)}^3}}} \ge 0,\forall x \in \left[ { - 1;1} \right]$
Nên $\dfrac{{\sqrt 3 }}{3} \le t \le \sqrt 3 $
Khi đó phương trình trở thành $3{t^2} + 2 = mt \Leftrightarrow 3t + \dfrac{2}{t} = m$
Xét hàm số $g\left( t \right) = 3t + \dfrac{2}{t}$.
Ta có $g'\left( t \right) = 3 - \dfrac{2}{{{t^2}}} = \dfrac{{3{t^2} - 2}}{{{t^2}}}$.
Cho $g'\left( t \right) = 0 \Rightarrow t = \dfrac{{\sqrt 6 }}{3}$
Bảng biến thiên:
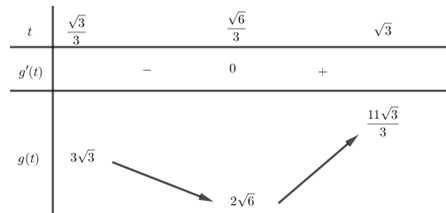
Dựa vào bảng biến thiên suy ra $2\sqrt 6 < m \le 3\sqrt 3 $.
Một ô tô chuyển động nhanh dần đều với vận tốc \(v\left( t \right) = 7t\) \(\left( {{\rm{m/s}}} \right)\). Đi được \(5\)\(\left( {\rm{s}} \right)\) người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc \(a = - 35\) \(\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\). Tính quãng đường của ô tô đi được từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn?
Quãng đường ô tô đi được trong \(5\)\(\left( {\rm{s}} \right)\) đầu là ${s_1} = \int\limits_0^5 {7t{\rm{d}}t} = 7\left. {\dfrac{{{t^2}}}{2}} \right|_0^5 = 87,5$ (mét)
Phương trình vận tốc của ô tô khi người lái xe phát hiện chướng ngại vật là \({v_{\left( 2 \right)}}\left( t \right) = 35 - 35t\) (m/s). Khi xe dừng lại hẳn thì \({v_{\left( 2 \right)}}\left( t \right) = 0 \Leftrightarrow 35 - 35t = 0 \Leftrightarrow t = 1\)
Quãng đường ô tô đi được từ khi phanh gấp đến khi dừng lại hẳn là \({s_2} = \int\limits_0^1 {\left( {35 - 35t} \right){\rm{d}}t} \)\( = \left. {\left( {35t - 35\dfrac{{{t^2}}}{2}} \right)} \right|_0^1\)\( = 17,5\) (mét)
Vậy quãng đường của ô tô đi được từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn là \(s = {s_1} + {s_2}\)\( = 87,5 + 17,5\)\( = 105\) (mét)
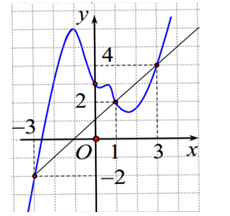
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị \(y = f'\left( x \right)\) cho như hình dưới đây. Đặt \(g\left( x \right) = 2f\left( x \right) - {\left( {x + 1} \right)^2}\). Mệnh đề nào dưới đây đúng.
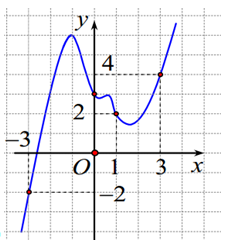
Ta có \(g\left( x \right) = 2f\left( x \right) - {\left( {x + 1} \right)^2}\)
\( \Rightarrow g'\left( x \right) = 2f'\left( x \right) - \left( {2x + 2} \right) = 0 \Leftrightarrow f'\left( x \right) = x + 1\).
Quan sát trên đồ thị ta có hoành độ giao điểm của \(f'\left( x \right)\) và \(y = x + 1\) trên khoảng \(\left( { - 3;3} \right)\) là \(x = 1\).
Vậy ta so sánh các giá trị \(g\left( { - 3} \right)\), \(g\left( 1 \right)\), \(g\left( 3 \right)\)
Xét \(\int\limits_{ - 3}^1 {g'\left( x \right)} {\rm{d}}x = 2\int\limits_{ - 3}^1 {\left[ {f'\left( x \right) - \left( {x + 1} \right)} \right]} {\rm{d}}x > 0\)
\( \Leftrightarrow g\left( 1 \right) - g\left( { - 3} \right) > 0 \Leftrightarrow g\left( 1 \right) > g\left( { - 3} \right)\)
Tương tự xét \(\int\limits_1^3 {g'\left( x \right)} {\rm{d}}x = 2\int\limits_1^3 {\left[ {f'\left( x \right) - \left( {x + 1} \right)} \right]} {\rm{d}}x < 0\)\( \Leftrightarrow g\left( 3 \right) - g\left( 1 \right) < 0 \Leftrightarrow g\left( 3 \right) < g\left( 1 \right)\)
Xét \(\int\limits_{ - 3}^3 {g'\left( x \right)} {\rm{d}}x = 2\int\limits_{ - 3}^1 {\left[ {f'\left( x \right) - \left( {x + 1} \right)} \right]} {\rm{d}}x + 2\int\limits_1^3 {\left[ {f'\left( x \right) - \left( {x + 1} \right)} \right]} {\rm{d}}x > 0\)
\( \Leftrightarrow g\left( 3 \right) - g\left( { - 3} \right) > 0 \Leftrightarrow g\left( 3 \right) > g\left( { - 3} \right)\).
Suy ra ta có \(g\left( 1 \right) > g\left( 3 \right) > g\left( { - 3} \right)\).
Vậy \(\mathop {\max }\limits_{\left[ { - 3;3} \right]} g\left( x \right) = g\left( 1 \right)\).
Cho hàm số \(f\left( x \right) \ne 0\); \(f'\left( x \right) = \left( {2x + 1} \right).{f^2}\left( x \right)\) và \(f\left( 1 \right) = - 0,5\).
Tính tổng \(f\left( 1 \right) + f\left( 2 \right) + f\left( 3 \right) + ... + f\left( {2017} \right) = \dfrac{a}{b}\); \(\left( {a \in \mathbb{Z};b \in \mathbb{N}} \right)\) với \(\dfrac{a}{b}\) tối giản. Chọn khẳng định đúng:
Ta có: \(f'\left( x \right) = \left( {2x + 1} \right).{f^2}\left( x \right)\)\( \Leftrightarrow \dfrac{{f'\left( x \right)}}{{{f^2}\left( x \right)}} = 2x + 1\)\( \Leftrightarrow \int {\dfrac{{f'\left( x \right)}}{{{f^2}\left( x \right)}}{\rm{d}}x} = \int {\left( {2x + 1} \right){\rm{d}}x} \)
\( \Leftrightarrow - \dfrac{1}{{f\left( x \right)}} = {x^2} + x + C\)\( \Rightarrow \dfrac{1}{{f\left( x \right)}} = - {x^2} - x - C\).
Lại có: \(f\left( 1 \right) = - 0,5\)\( \Rightarrow - 2 = - {1^2} - 1 - C\)\( \Rightarrow C = 0\).
Vậy \(\dfrac{1}{{f\left( x \right)}} = - \left( {{x^2} + x} \right) = - x\left( {x + 1} \right)\) hay \( - f\left( x \right) = \dfrac{1}{{x\left( {x + 1} \right)}}\).
Ta có: \( - f\left( 1 \right) - f\left( 2 \right) - f\left( 3 \right) - ... - f\left( {2017} \right)\)\( = \dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{2017.2018}}\)
\( = 1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{2017}} - \dfrac{1}{{2018}}\)\( = 1 - \dfrac{1}{{2018}}\)\( = \dfrac{{2017}}{{2018}}\).
Vậy \(f\left( 1 \right) + f\left( 2 \right) + f\left( 3 \right) + ... + f\left( {2017} \right) = \dfrac{{ - 2017}}{{2018}}\) hay \(a = - 2017\), \(b = 2018\) \( \Rightarrow b - a = 4035\).
Đặt \(S\) là diện tích của hình phẳng giới hạn bởi đồ thị của hàm số \(y = 4 - {x^2}\), trục hoành và đường thẳng \(x = - 2\), \(x = m\), \(\left( { - 2 < m < 2} \right)\). Tìm số giá trị của tham số \(m\) để \(S = \dfrac{{25}}{3}\).
Ta có \(S = \int\limits_{ - 2}^m {\left| {4 - {x^2}} \right|{\rm{d}}x} = \dfrac{{25}}{3}\).
Phương trình hoành độ giao điểm: \(4 - {x^2} = 0 \Leftrightarrow x = \pm 2\)
Do \( - 2 < x < m < 2\) nên \(4 - {x^2} > 0,\forall x \in \left( { - 2;m} \right)\) ta có:
\(\begin{array}{l}S = \int\limits_{ - 2}^m {\left| {4 - {x^2}} \right|dx} = \frac{{25}}{3}\\ \Leftrightarrow \int\limits_{ - 2}^m {\left( {4 - {x^2}} \right)dx} = \frac{{25}}{3}\\ \Leftrightarrow \left. {\left( {4x - \frac{{{x^3}}}{3}} \right)} \right|_{ - 2}^m = \frac{{25}}{3}\\ \Leftrightarrow 4m - \frac{{{m^3}}}{3} + 8 - \frac{8}{3} = \frac{{25}}{3}\\ \Leftrightarrow - {m^3} + 12m - 9 = 0\\ \Leftrightarrow {m^3} - 12m + 9 = 0\\ \Leftrightarrow \left( {m - 3} \right)\left( {{m^2} + 3m - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 3 = 0\\{m^2} + 3m - 3 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m = 3\left( {loai} \right)\\m = \frac{{ - 3 + \sqrt {21} }}{2}\left( {TM} \right)\\m = \frac{{ - 3 - \sqrt {21} }}{2}\left( {KTM} \right)\end{array} \right.\end{array}\)
Vậy chỉ có \(m = \dfrac{{\sqrt {21} - 3}}{2}\) thỏa mãn bài toán.
Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và thỏa mãn $f\left( x \right) > 0$, $\forall x \in \mathbb{R}$. Biết $f\left( 0 \right) = 1$ và $\dfrac{{f'\left( x \right)}}{{f\left( x \right)}} = 2 - 2x$. Tìm các giá trị thực của tham số $m$ để phương trình $f\left( x \right) = m$ có hai nghiệm thực phân biệt.
Ta có $\dfrac{{f'\left( x \right)}}{{f\left( x \right)}} = 2 - 2x$$ \Rightarrow \int {\dfrac{{f'\left( x \right)}}{{f\left( x \right)}}} {\rm{d}}x = \int {\left( {2 - 2x} \right){\rm{d}}x} $
$ \Leftrightarrow \ln f\left( x \right) = 2x - {x^2} + C$$ \Leftrightarrow f\left( x \right) = {e^{2x - {x^2}+C}}$ $ \Leftrightarrow f\left( x \right) = A.{e^{2x - {x^2}}}$ với $A=e^C$
Mà \(f\left( 0 \right) = 1\) suy ra \(f\left( x \right) = {e^{2x - {x^2}}}\).
Ta có \(2x - {x^2} = 1 - \left( {{x^2} - 2x + 1} \right)\)\( = 1 - {\left( {x - 1} \right)^2} \le 1\).
Suy ra \(0 < {e^{2x - {x^2}}} \le e\) và ứng với một giá trị thực \(t < 1\) thì phương trình \(2x - {x^2} = t\) sẽ có hai nghiệm phân biệt.
Vậy để phương trình $f\left( x \right) = m$ có \(2\) nghiệm phân biệt khi \(0 < m < {e^1} = e\).
Trong hệ trục tọa độ \(Oxy\), cho parabol \(\left( P \right):y = {x^2}\) và hai đường thẳng \(y = a\), \(y = b\) \(\left( {0 < a < b} \right)\) (hình vẽ). Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi parabol \(\left( P \right)\) và đường thẳng \(y = a\) (phần tô đen); \(\left( {{S_2}} \right)\) là diện tích hình phẳng giới hạn bởi parabol \(\left( P \right),\) đường thẳng $y=a$ và đường thẳng \(y = b\) (phần gạch chéo). Với điều kiện nào sau đây của \(a\) và \(b\) thì \({S_1} = {S_2}\)?
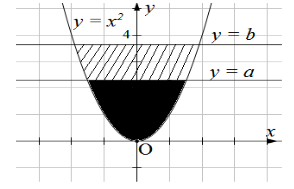
Phương trình hoành độ giao điểm của parabol \(\left( P \right):y = {x^2}\) với đường thẳng \(y = b\) là
\({x^2} = b \Leftrightarrow x = \pm \sqrt b \).
Phương trình hoành độ giao điểm của parabol \(\left( P \right):y = {x^2}\) với đường thẳng \(y = a\) là
\({x^2} = a \Leftrightarrow x = \pm \sqrt a \).
Diện tích hình phẳng giới hạn bởi parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(y = b\) là
$S = 2\int\limits_0^{\sqrt b } {\left( {b - {x^2}} \right){\mathop{\rm d}\nolimits} x} $$ = \left. {2\left( {bx - \dfrac{{{x^3}}}{3}} \right)} \right|_0^{\sqrt b }$$ = 2\left( {b\sqrt b - \dfrac{{b\sqrt b }}{3}} \right)$$ = \dfrac{{4b\sqrt b }}{3}$.
Diện tích hình phẳng giới hạn bởi parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(y = a\)(phần tô màu đen) là ${S_1} = 2\int\limits_0^{\sqrt a } {\left( {a - {x^2}} \right){\mathop{\rm d}\nolimits} x} $$ = \left. {2\left( {ax - \dfrac{{{x^3}}}{3}} \right)} \right|_0^{\sqrt a }$$ = 2\left( {a\sqrt a - \dfrac{{a\sqrt a }}{3}} \right)$$ = \dfrac{{4a\sqrt a }}{3}$.
Do đó \(S = 2{S_1}\)\( \Leftrightarrow \dfrac{{4b\sqrt b }}{3} = 2.\dfrac{{4a\sqrt a }}{3}\)\( \Leftrightarrow {\left( {\sqrt b } \right)^3} = 2{\left( {\sqrt a } \right)^3}\)\( \Leftrightarrow \sqrt b = \sqrt[3]{2}\sqrt a \)\( \Leftrightarrow b = \sqrt[3]{4}a\).
Cho hàm số \(f\left( x \right)\) liên tục, không âm trên đoạn \(\left[ {0;\dfrac{\pi }{2}} \right]\), thỏa mãn \(f\left( 0 \right) = \sqrt 3 \) và \(f\left( x \right).f'\left( x \right) = \cos x.\sqrt {1 + {f^2}\left( x \right)} \), \(\forall x \in \left[ {0;\dfrac{\pi }{2}} \right]\). Tìm giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {\dfrac{\pi }{6};\dfrac{\pi }{2}} \right]\).
Từ giả thiết \(f\left( x \right).f'\left( x \right) = \cos x.\sqrt {1 + {f^2}\left( x \right)} \)
\( \Rightarrow \int {\dfrac{{f\left( x \right).f'\left( x \right)}}{{\sqrt {1 + {f^2}\left( x \right)} }}{\rm{d}}x} = \sin x + C\)
Đặt \(t = \sqrt {1 + {f^2}\left( x \right)} \Rightarrow {t^2} = 1 + {f^2}\left( x \right)\) \( \Rightarrow t dt = f\left( x \right)f'\left( x \right){\rm{d}}x\)
Thay vào ta được \(\int {dt} = \sin x + C \Rightarrow t = \sin x + C\)\( \Rightarrow \sqrt {1 + {f^2}\left( x \right)} = \sin x + C\)
Do \(f\left( 0 \right) = \sqrt 3 \)\( \Rightarrow C = 2\).
Vậy \(\sqrt {1 + {f^2}\left( x \right)} = \sin x + 2 \Rightarrow {f^2}\left( x \right) = {\sin ^2}x + 4\sin x + 3\)
\( \Rightarrow f\left( x \right) = \sqrt {{{\sin }^2}x + 4\sin x + 3} \), vì hàm số \(f\left( x \right)\) liên tục, không âm trên đoạn \(\left[ {0;\dfrac{\pi }{2}} \right]\).
Ta có \(\dfrac{\pi }{6} \le x \le \dfrac{\pi }{2} \Rightarrow \dfrac{1}{2} \le \sin x \le 1\), xét hàm số \(g\left( t \right) = {t^2} + 4t + 3\) có hoành độ đỉnh \(t = - 2\) loại.
Suy ra \(\mathop {\max }\limits_{\left[ {\dfrac{1}{2};1} \right]} g\left( t \right) = g\left( 1 \right) = 8\), \(\mathop {\min }\limits_{\left[ {\dfrac{1}{2};1} \right]} g\left( t \right) = g\left( {\dfrac{1}{2}} \right) = \dfrac{{21}}{4}\)
Suy ra \(\mathop {\max }\limits_{\left[ {\dfrac{\pi }{6};\dfrac{\pi }{2}} \right]} f\left( x \right) = f\left( {\dfrac{\pi }{2}} \right) = 2\sqrt 2 \), \(\mathop {\min }\limits_{\left[ {\dfrac{\pi }{6};\dfrac{\pi }{2}} \right]} f\left( x \right) = g\left( {\dfrac{\pi }{6}} \right) = \dfrac{{\sqrt {21} }}{2}\)
Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v\left( t \right) = \dfrac{1}{{100}}{t^2} + \dfrac{{13}}{{10}}t\left( {m/s} \right)\), trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 10 giây so với A và có gia tốc bằng \(a\left( {m/{s^2}} \right)\) (\(a\) là hằng số). Sau khi B xuất phát được 15 giây thì đuổi kịp A. Vận tốc của B tại thời điểm đuổi kịp A bằng
Bước 1: Tìm $v_B(t)$
Ta có \({v_B}\left( t \right) = \int {adt} = at + C,{v_B}\left( 0 \right) = 0\)
\( = > C = 0 = > {v_B}\left( t \right) = at\)
Bước 2: Tính quãng đường A đi được trong 25 giây
Quãng đường chất điểm A đi được trong 25 giây là
\({S_A} = \int\limits_0^{25} {\left( {\dfrac{1}{{100}}{t^2} + \dfrac{{13}}{{10}}t} \right)dt} \) \( = \left. {\left( {\dfrac{1}{{300}}{t^3} + \dfrac{{13}}{{60}}{t^2}} \right)} \right|_0^{25} = \dfrac{{375}}{2}\)
Bước 3: Tính quãng đường B đi được trong 15 giây
Quãng đường chất điểm B đi được trong 15 giây là
\({S_B} = \int\limits_0^{15} {at} .dt = \left. {\dfrac{{a{t^2}}}{2}} \right|_0^{15} = \dfrac{{225a}}{2}\)
Bước 4: Tìm a và $v_B(15)$
Ta có: \(\dfrac{{375}}{2} = \dfrac{{225a}}{2} \Leftrightarrow a = \dfrac{5}{3}\)
Vận tốc của B tại thời điểm đuổi kịp A là \(v_B\left( {15} \right) = \dfrac{5}{3}.15 = 25\left( {m/s} \right)\)

