Cho hình phẳng \(D\) giới hạn bởi đường cong \(y = {{\rm{e}}^{x - 1}}\), các trục tọa độ và phần đường thẳng \(y = 2 - x\) với \(x \ge 1\). Tính thể tích khối tròn xoay tạo thành khi quay quanh trục hoành.
Trả lời bởi giáo viên
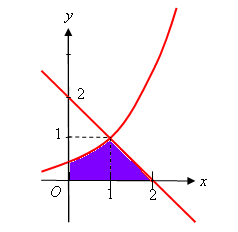
Phương trình hoành độ giao điểm của đường cong \(y = {{\rm{e}}^{x - 1}}\) và đường thẳng \(y = 2 - x\): ${{\rm{e}}^{x - 1}} = 2 - x \Leftrightarrow x = 1$.
(Vì \(y = {{\rm{e}}^{x - 1}}\) là hàm đồng biến và \(y = 2 - x\) là hàm nghịch biến trên tập xác định \(\mathbb{R}\) nên phương trình có tối đa \(1\) nghiệm. Mặt khác $x = 1$ thỏa mãn pt nên đó là nghiệm duy nhất của pt đó).
Đường thẳng \(y = 2 - x\) cắt trục hoành tại điểm có hoành độ \(x = 2\).
\(V = \pi \int\limits_0^1 {{{\left( {{{\rm{e}}^{x - 1}}} \right)}^2}{\rm{d}}x} + \pi \int\limits_1^2 {{{\left( {2 - x} \right)}^2}{\rm{d}}x} \)\( = \left. \dfrac{1}{2}{\pi {{\rm{e}}^{2x - 2}}} \right|_0^1 + \left. {\pi \left( {\dfrac{{{x^3}}}{3} - 2x + 4} \right)} \right|_1^2 = \dfrac{{\pi \left( {5{{\rm{e}}^2} - 3} \right)}}{{6{{\rm{e}}^2}}}\)
Hướng dẫn giải:
- Vẽ phác đồ thị các hàm số \(y = {{\rm{e}}^{x - 1}}\) và \(y = 2 - x\) trên cùng một hệ trục tọa độ.
- Tính thể tích vật thể tròn xoay theo công thức \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)

